11. Выбор двигателя

В курсовом проекте предлагается использовать электрический двигатель постоянного тока независимого возбуждения. Такой двигатель имеет линейную статическую характеристику, что упрощает расчет установившегося режима и режима разбега.

Двигатель выбирают по необходимой (эквивалентной) мощности, т.е. такой мощности, которая требуется для того, чтобы механизм, испытывающий воздействие заданных сил, совершал требуемые движения.

Выбор двигателя производим по среднеквадратичному значению момента из каталога стандартных двигателей.

С помощью MathCad, основываясь на результатах силового расчета, находим значение эквивалентной мощности. В данном случае:

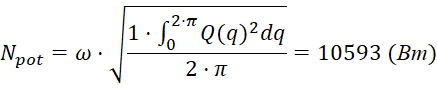
По каталогу выбираем следующий двигатель:

Типоразмер двигателя: 2ПН225L

Мощность Nдн: 18500 Вт

Скорость nдн: 750 об/мин

Номинальный ток Iн: 88 А

Номинальное напряжение uн: 220 В

Сопротивление R: 0,095 Ом

Индуктивность L: 0.0024 Гн

Момент инерции ротора Jp: 0.6

Коэффициент перегрузки γ: 1,8

Находим номинальный момент на двигателе ( ):

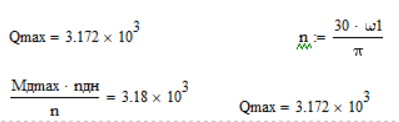
Так как Q2>Qmax, то выбранный двигатель удовлетворяет условиям.

Определяем параметры двигателя:

а) число оборотов в минуту на холостом ходу (об/мин):

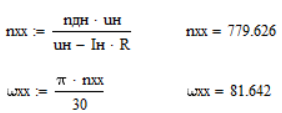
б) электромагнитная постоянная времени (c):

в) крутизну статистической характеристики двигателя ( ):

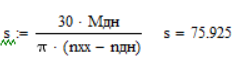
Определяем передаточное число редуктора:

12.Динамическое исследование машинного агрегата (ма).

12.1.Задачи динамического исследования.

Машинный агрегат состоит из двигателя, передаточного и исполнительного механизмов. Динамический расчет машинного агрегата связан с определением и исследованием стационарного решения системы дифференциальных уравнений.

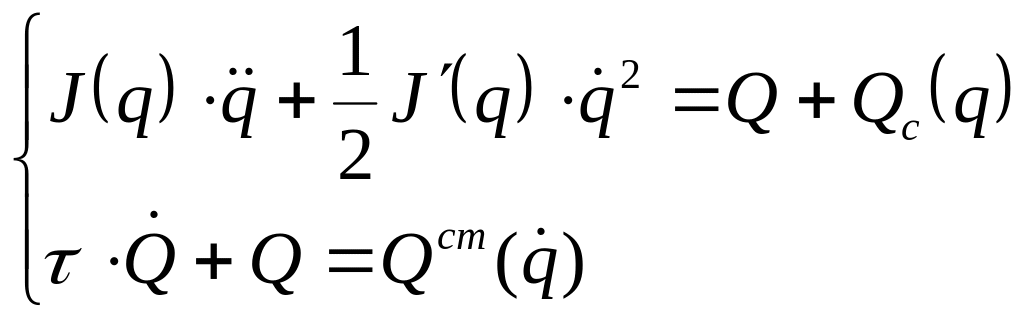
Уравнение представляет собой уравнение механической системы агрегата, рассматриваемой как механизм с жесткими звеньями, обладающими одной степенью свободы (подвижности). В этом уравнении q – обобщенная координата, в качестве которой выбран угол поворота входного звена исполнительного механизма; J(q) – приведенный момент инерции механической системы;

Q_c(q) – приведенный момент сил сопротивления.

Второе уравнение является приведенной динамической характеристикой двигателя.

Здесь τ– электромагнитная постоянная времени двигателя; - приведенная статическая характеристика двигателя, разрешенная относительно момента.

12.2.Построение динамической и математической модели ма

Машина включает в себя двигатель, передаточный и исполнительный механизмы.

Динамическая модель машинного агрегата:

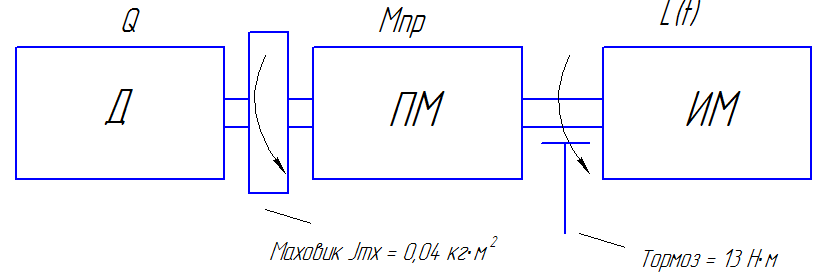
Рис.12.1. Динамическая модель машинного агрегата

а) Приведенный момент инерции как коэффициент при половине квадрата обобщенной скорости в выражении кинетической энергии механической системы:

Приведенный момент инерции с учетом противовесов, ротора двигателя, и момента инерции передаточного механизма.

Полученная функция с целью упрощения динамических расчетов раскладывается в ряд Фурье с точностью до пяти гармоник.

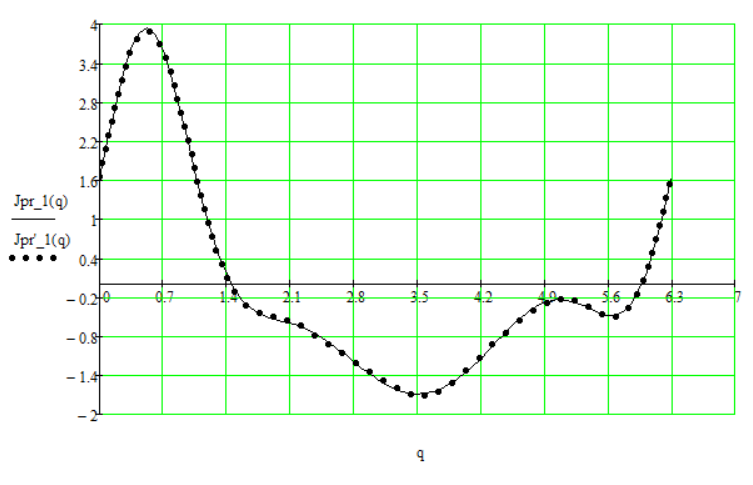
Рис. 12.2. Графики переменной части приведенного момента инерции

На графике:

Jpr_1 – график переменной части приведенного момента инерции, найденного через кинетическую энергию. Jpr’_1 – график, разложенный в ряд Фурье.

б) Производная от приведенного момента инерции по обобщенной координате:

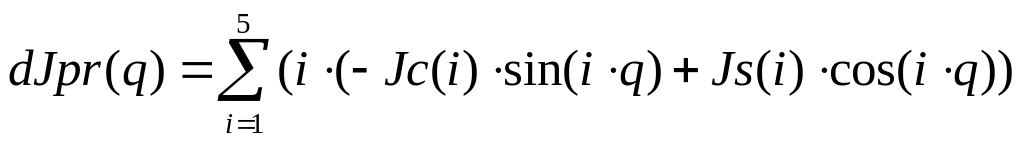
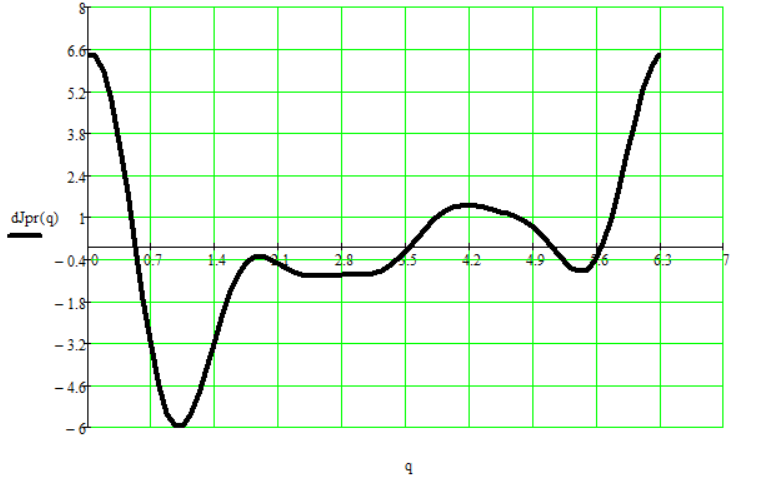
Рис. 12.3. График производной от приведенного момента инерции

в) Приведенный момент сил сопротивления определяется как коэффициент при вариации обобщенной координаты в выражении для возможной работы активных сил сопротивления (рабочей нагрузки и сил тяжести):

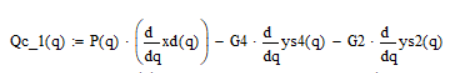
С учетом противовесов:

Функция раскладывается в ряд Фурье с точностью до пяти гармоник:

;

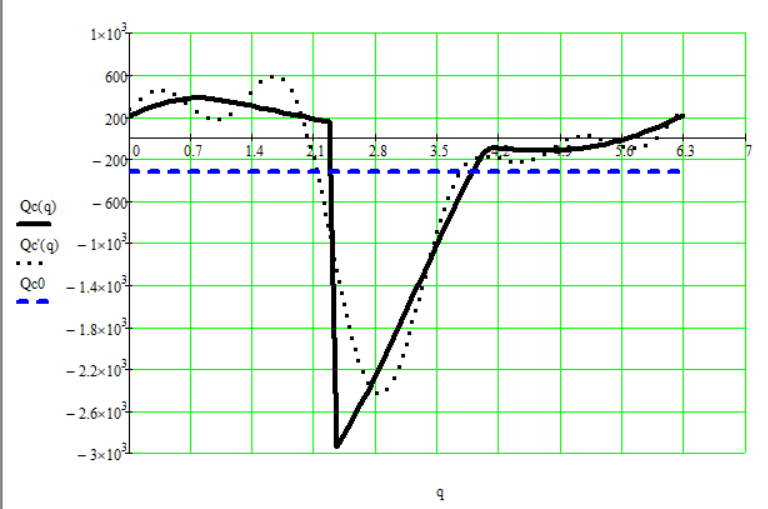
Рис. 12.4. График приведенного момента cил сопротивления.

На графике:

Qc(q) - при расчёте по формуле коэффициента вариации обобщённой координаты

Qс’(q) - при расчёте разложением в ряд Фурье

Qc0- среднее значение.

г)Приведенная статическая характеристика двигателя определяется как обобщенная сила из уравнения

Где уравнение статической характеристики электродвигателя постоянного тока независимого возбуждения

- угловая скорость холостого хода ротора двигателя.

Тогда

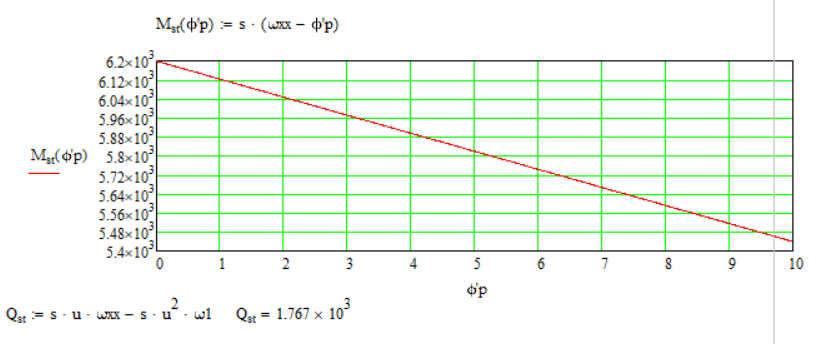
Рис. 12.5. Приведенная статическая характеристика двигателя