9.3.Задание графика рабочей нагрузки
Построим график зависимости приложенной нагрузки на выходное звено P(q).
График нагрузки строим в соответствии с нагрузочной диаграммой из задания.
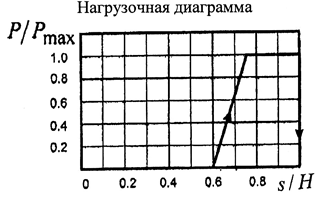
Рис.9.1.Индикаторная диаграмма
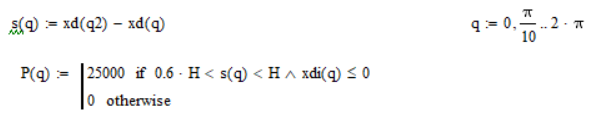
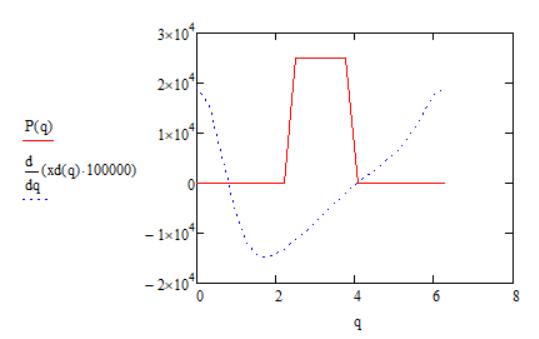
Рис. 9.2. График рабочей нагрузки
9.4 Решение уравнений кинетостатики
На схеме механизма (рис.10.3.) изобразим все силы инерции, силы тяжести и моменты сил инерции для всех звеньев механизма.
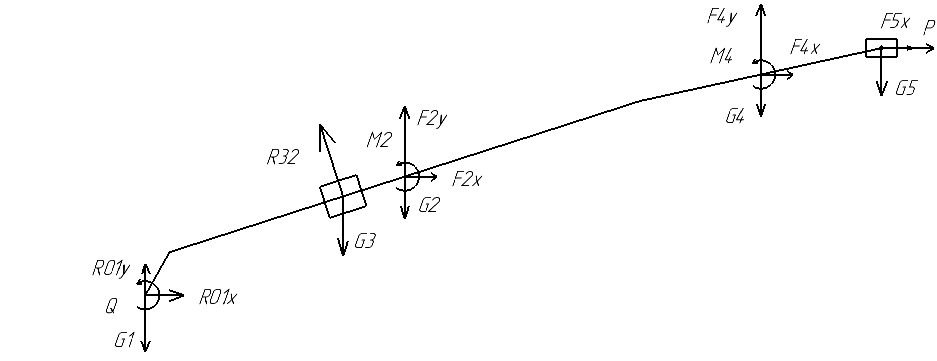
Рис. 9.3. Схема механизма со всеми силами
Рассмотрим отдельно структурные группы механизма. Отрываем структурную группу от механизма и в местах отрыва действие других звеньев заменяем реакциями опор.
Определим реакции в кинематических парах для звеньев 4 и 5:
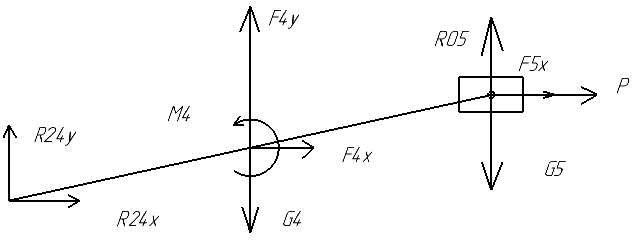
Рис.9.4. Звено 4 и 5
Определим реакции в кинематических парах для звеньев 4 и 5:
Запишем уравнения равновесия для плоской системы
Решаем систему
уравнений равновесия в Маткаде и находим
неизвестные реакции опор
.
Определим реакции в кинематических парах для звеньев 2 и 3:
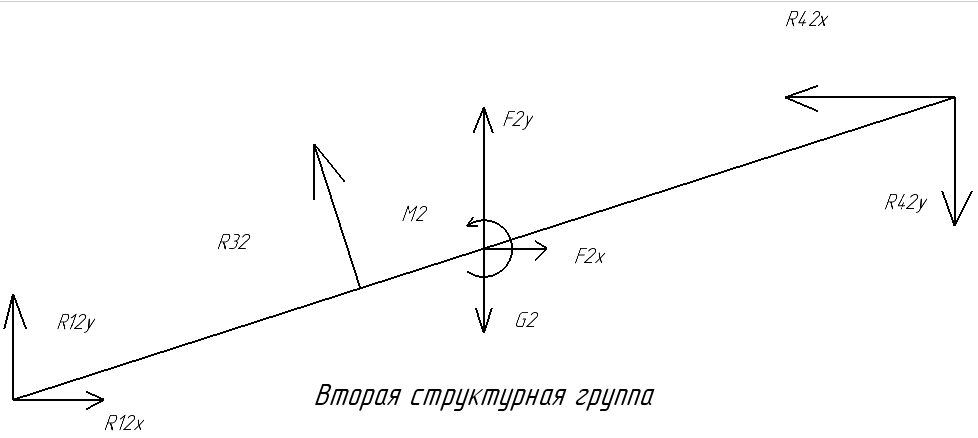
Рис. 9.5. Звенья 2 и 3
Запишем уравнения
равновесия для плоской системы. В данной
системе реакции
равны и противоположно направлены
реакциям
соответственно:
Решаем
систему уравнений равновесия в Маткаде
и находим неизвестные реакции опор.
Определим реакции в кривошипе и найдем движущий момент Q:
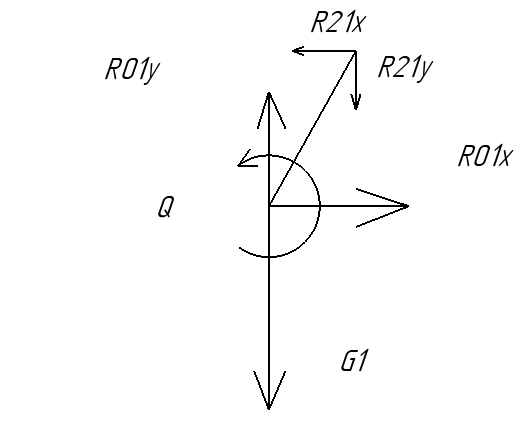
Рис. 9.6.— Звено 1
Запишем уравнения равновесия для плоской системы (момент берем относительно точки О)
В данной системе
реакции
и
равны и противоположно направлены
реакциям
и
соответственно:
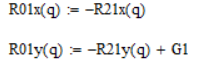
Решаем систему в
Маткаде и находим неизвестные реакции
опор
и
,
а также движущий момент Q.
9.5.Нахождение движущего момента из общего уравнения динамики
Метод заключается в том, что малая работа всех активных сил на возможном перемещении равна нулю.
Найдем движущий момент:
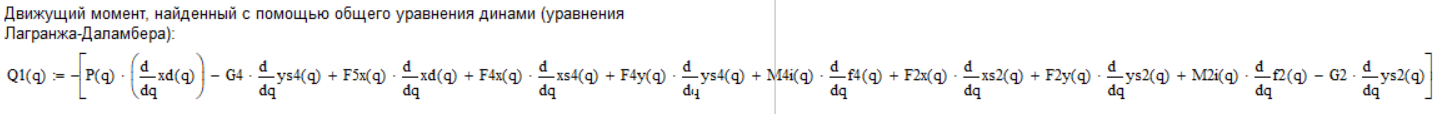
Для проверки силового анализа наложим графики зависимости движущего момента Q(q), полученного из общего уравнения динамики и кинетостатическим методом (рис.9.7).
Как видно из рис.9.7. графики зависимости движущего момента для двух методов силового анализа совпали, поэтому можно говорить о правильности анализа механизма.
График зависимости q1 и q от q
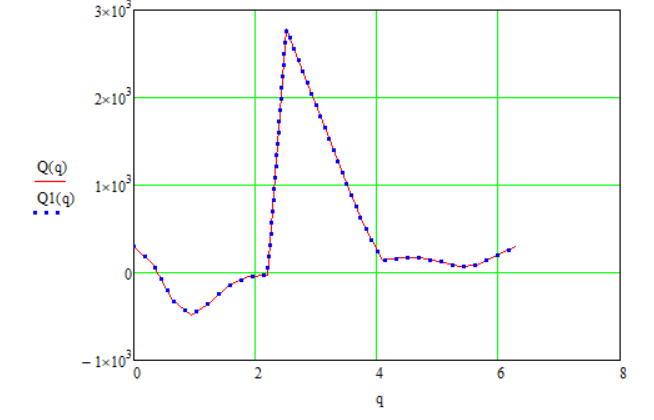
Рис. 9.7. Графики движущего момента
9.6.Статика
Звено 4 и 5:
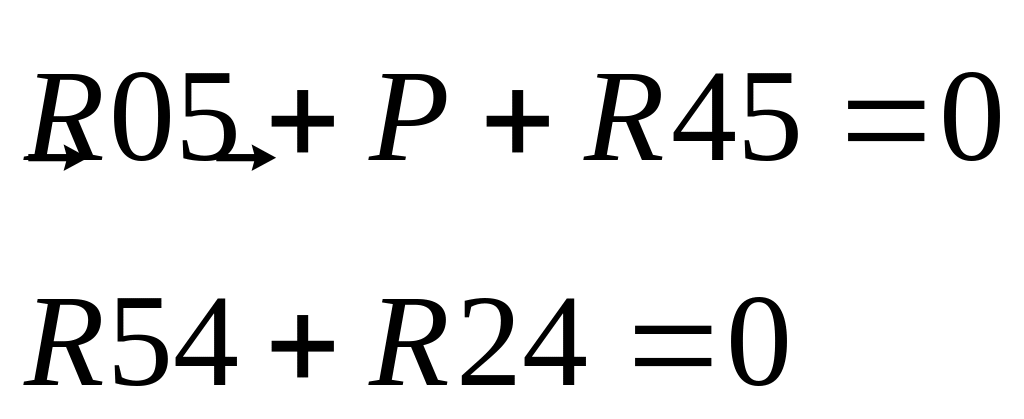
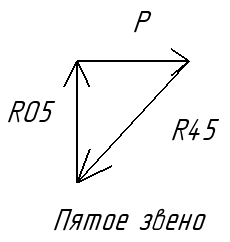
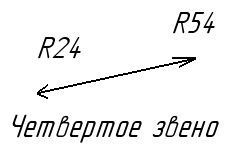
Рис.9.8. Статика 4 и 5.
Звено 2 и 3:
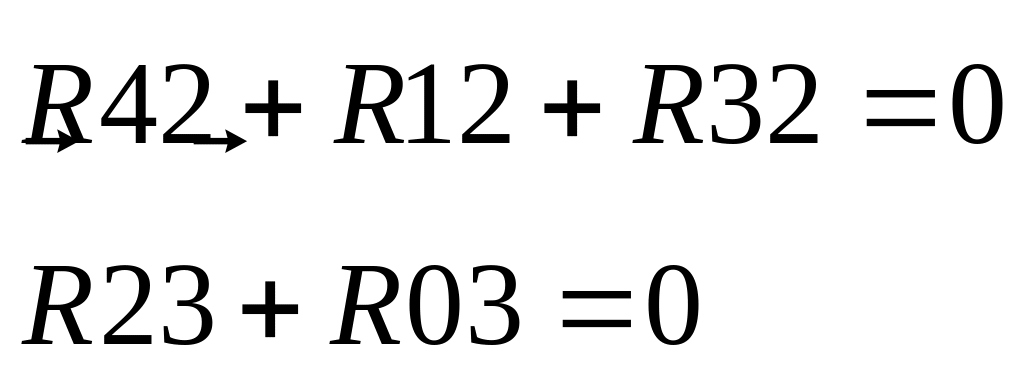
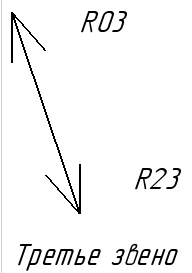
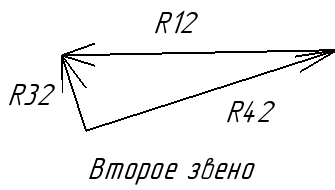
Рис.9.9. Статика 2 и 3.
Звено 1:
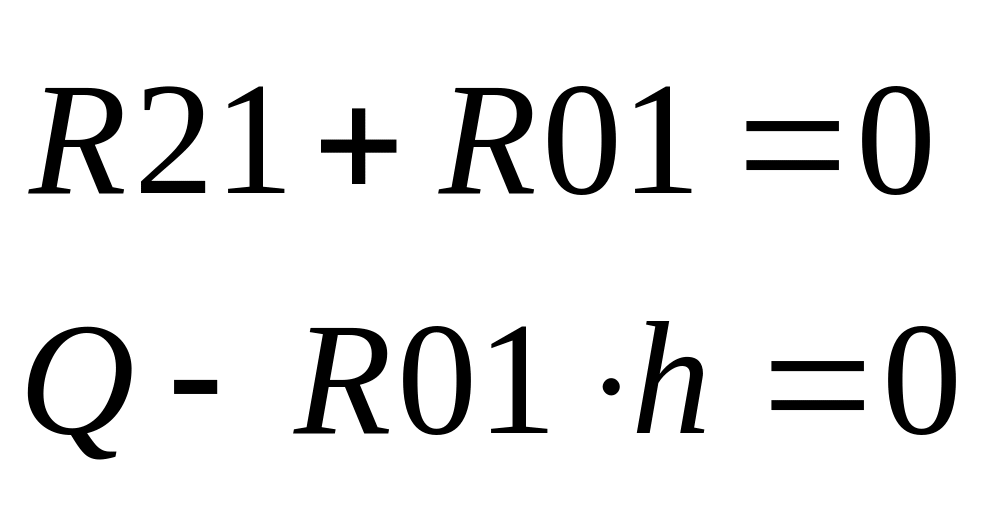
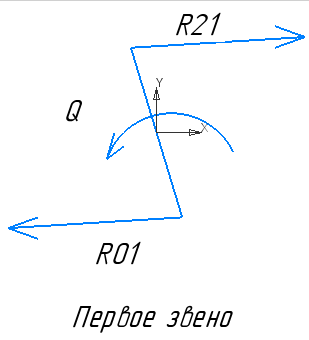
Рис.9.10. Статика звено 1.
10. Внешняя виброактивность механизма и машины
Свойство механизма во время движения воздействовать на корпус машины переменными силами называется внешней виброактивностью. Мерой внешней виброактивности механизма являются усилия, действующие на стойку (корпус) машины, численно равные главным векторам и главным момента внешних активных сил и сил инерции:
В большинстве случаев активные силы, приложенные к звеньям механизма, оказываются по отношению к машине в целом силами внутренними, поэтому:
В случае механизма, рассматриваемого в данной работе:
Годограф главного вектора сил инерции
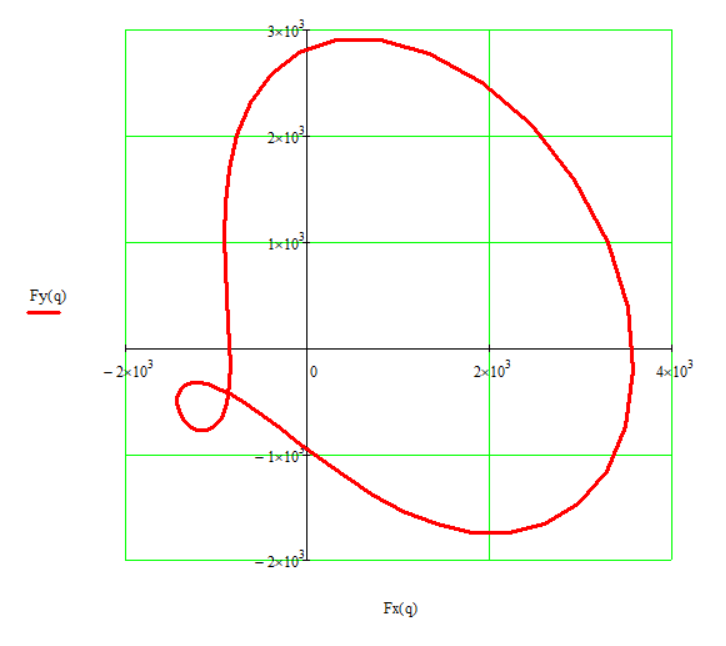
Рис. 10.1. Годограф главного вектора сил инерции
В плоском механизме ограничиваются определением составляющих главного вектора и главного момента внешних реакций, лежащих в плоскости движения
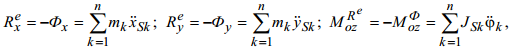
где k = 1,2,...,n - номер подвижного звена; Sk - центр масс k- го звена
Одним из методов уменьшения внешней виброактивности машины является уравновешивание механизмов. Механизм называется уравновешенным, если динамические усилия, прикладываемые к стойке этим механизмом, образуют уравновешенную систему сил.
При внутренних активных силах для уравновешенности механизма необходимо выполнение условий:
;
,
Сводящих задачу
уравновешивания механизма к задаче
уравновешивания сил инерции. Здесь m
и S
– масса и центр масс механизма;
- главный момент количества движения
механизма.
Вышеприведенные условия будут выполняться, если координаты центра масс и главный момент количества движения будут неизменными. В плоском механизме чаще всего ограничиваются выполнением условий
xs=const; ys=const.
Эти условия достигаются путем перераспределения масс механизма. Для этого к его звеньям присоединяют дополнительные массы, называемые противовесами. Противовесы чаще всего не устраняют, а уменьшают переменные усилия, действующие на стойку, т.е. решают задачу частичного уравновешивания.
Методом решения данной задачи были рассчитаны массы противовесов и углы их установки.
Разложим в ряд
Фурье:
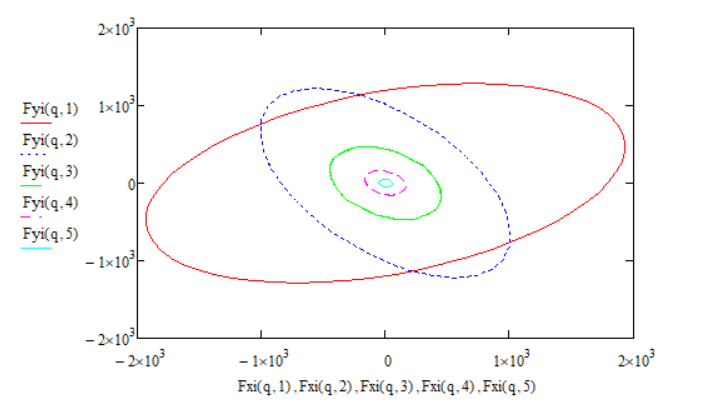
Рис. 10.2. Пять эллиптических гармоник разложения функции главного вектора сил инерции в ряд Фурье
Уравновесим
:
Разложим на две
круговые гармоники:
:
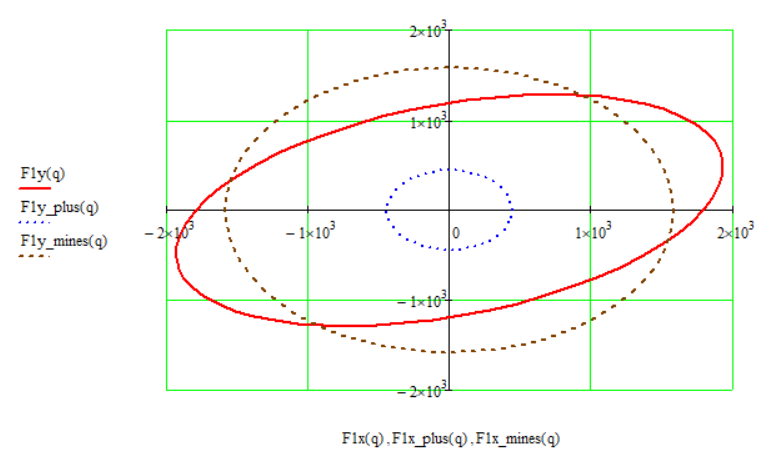
Рис. 10.3. Разложение первой эллиптической гармоники на две круговые гармоники
Коэффициенты векторов круговых гармоник связаны с коэффициентами эллиптической гармоники следующими зависимостями:
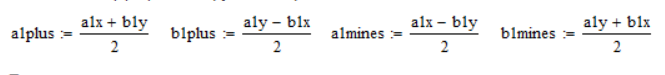
Модули круговых гармоник:
Смысл уравновешивания механизма на основе гармонического анализа заключается в том, что эллиптическую гармонику разлагают на две круговые гармоники, а затем каждую из круговых гармоник уравновешивают с помощью противовесов, установленных на кривошипе и на зубчатых колесах.
Для этого определяют массы противовесов (кг):
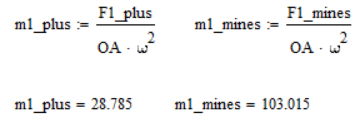
Начальные углы установки противовесов (град):
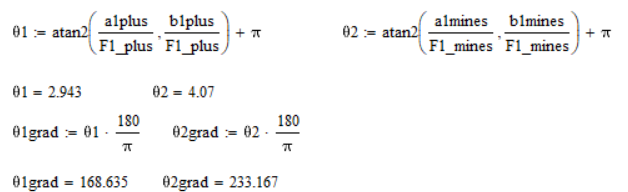
Усилия, передаваемые на корпус машины, после постановки противовесов:
Годограф главного вектора сил инерции до уравновешивания механизма и после:
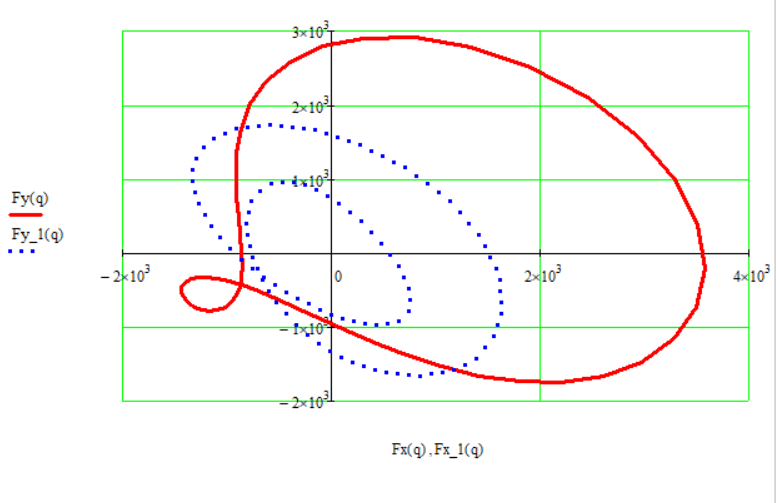
Рис. 10.4. Годограф главного вектора сил инерции до и после уравновешивания
Схема установки вращающихся противовесов
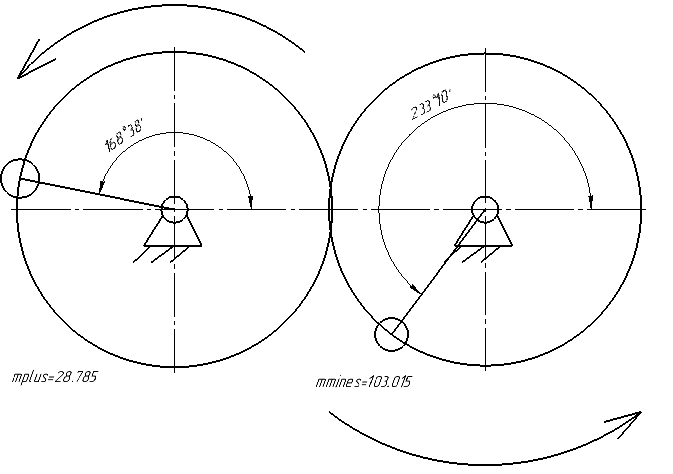
Рис. 10.5. Схема установки вращающихся противовесов
В результате установки противовесов годограф главного вектора сил инерции существенно изменился. Для сравнения с первоначальным годографом (до уравновешивания) изобразили годографы на одном графике.
Мы ограничились установкой двух вращающихся противовесов уменьшающих первую гармонику неуравновешенной силы, но не обеспечивающих полное ее устранение.
Устанавливая на дополнительных осях вращения противовесы, вращающиеся с постоянной угловой скоростью можно уравновесить аналогичным путем другие гармоники динамических реакций. Из-за сложности конструкции такое уравновешивание применяется только в исключительных случаях.
Установка противовесов не значительно повышает массу конструкции, и обоснована и рациональна с точки зрения динамических характеристик машины.