4 сем / лаба10 вар 11

Санкт-Петербургский Политехнический университет Петра Великого

Институт машиностроения, материалов и транспорта

Высшая школа машиностроения

ОТЧЕТ

по лабораторной работе № 10

Дисциплина: Вычислительная математика

Тема: Приближенное численное интегрирование

(Вариант 11)

Студент группы 3331505/10001 Гричачина А.А.

Преподаватель Кожанова Ю.В.

Санкт-Петербург

2023 г.

Задание

Точность всех вычислений в задании – .

1. Найти точное значение .

2. Разбить заданный промежуток на интервалов ( ). Перевести заданную функцию в дискретный аналог с шагом путем округления до заданной точности ее значений в узлах.

3. Рассчитать в Excel конечные разности для нахождения средних значений второй и четвертой производных в интервале интегрирования

4. Рассчитать в MathCAD значение интеграла для дискретно заданной функции по различным формулам приближенного интегрирования, приведенным в теоретической части и определить точность полученных результатов для каждого метода.

5. Сравнить результаты приближенных расчетов в MathCAD с точным значением интеграла и найти относительные погрешности приближенного интегрирования каждым методом.

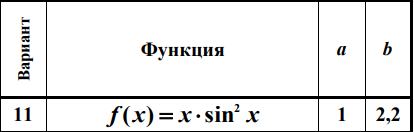
Рисунок 1 Задание первого варианта

Целью работы является закрепление знаний, полученных в лекционном курсе «Вычислительная математика» по разделу «Приближенное интегрирование», приобретение навыков использования соответствующих численных методов с применением программных средств автоматизации вычислений.

Краткие теоретические сведенья

Задача приближенного интегрирования возникает для сложных аналитических функций или функций, заданных дискретными данными. Методы численного интегрирования основаны на аппроксимации определенного интеграла суммой составных площадей. Численное интегрирование в отличие от численного дифференцирования является устойчивой процедурой и имеет тенденцию снижения влияния погрешности исходных данных на конечный результат. В общем виде задача состоит в нахождении величины .

Решение методом сеток в MathCAD

Задание пределов интегрирования, задание дискретного аналога функции и получение вектора y показаны на рисунке 2.

Рисунок 2 Задание исходных данных

В Exel рассчитываем конечные разности и находим средине значения второй и четвертых производных в интервале интегрирования, как показано на рисунке 3.

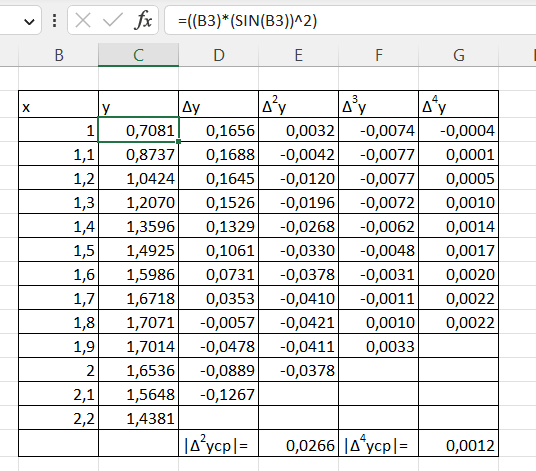
Рисунок 3 Таблица в Excel

Метод левых и правых прямоугольников, а так же точность данного метода показано на рисунке 4.

Рисунок 4 Нахождение значения интеграла методом прямоугольников

Метод трапеций и вычисление погрешности данного метода показано 5.

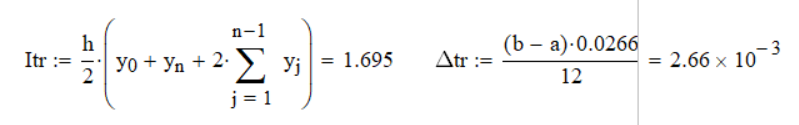
Рисунок 5 Нахождение значения интеграла методом трапеций

Метод Симпсона и погрешность данного метода, а так же вычисление погрешности по Рунге с новым шагом показано на рисунке 6.

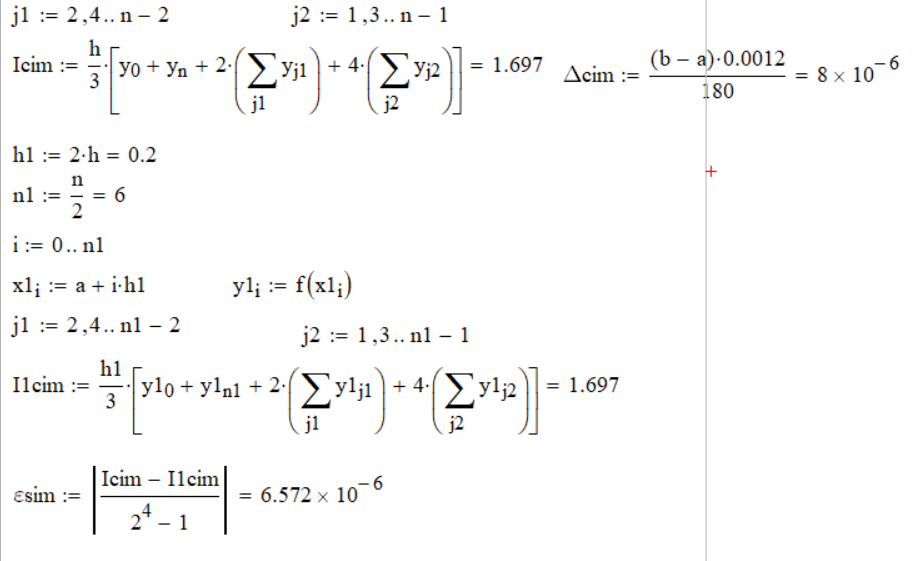
Рисунок 6 Вычисление методом Симпсона

Вывод: в результате работы было найдено приближенное значение интегрирования заданной функции с заданными дискретными данными.