4 сем / лаба9 вар 1

Санкт-Петербургский Политехнический университет Петра Великого

Институт машиностроения, материалов и транспорта

Высшая школа машиностроения

ОТЧЕТ

по лабораторной работе № 9

Дисциплина: Вычислительная математика

Тема: Решение задачи Дирихле для уравнения Лапласа

(Вариант 1)

Студент группы 3331505/10001 Гричачина А.А.

Преподаватель Кожанова Ю.В.

Санкт-Петербург

2023 г.

Задание

В MathCAD методом сеток найти приближенное решение уравнения Лапласа в заданной области с указанными граничными условиями, принять

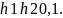
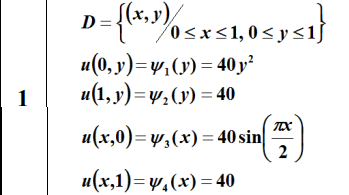
Рисунок 1 Задание первого варианта

Целью работы является закрепление знаний, полученных в лекционном курсе «Вычислительная математика» по разделу «Численные методы решения дифференциальных уравнений в частных производных», приобретение навыков использования соответствующих численных методов с применением программных средств автоматизации вычислений.

Краткие теоретические сведенья

Уравнение относительно неизвестной функции u(x, y) двух или более независимых переменных, которое содержит частные производные этой функции, называется уравнением в частных производных. В общем виде линейное уравнение в частных производных второго порядка относительно функции двух независимых переменных u(x, y) записывается так:

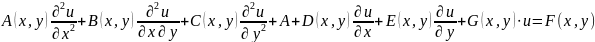
Все коэффициенты и правая часть уравнения являются константами или функциями независимых переменных x и y.

Решение методом сеток в MathCAD

Задание исходных данных (краевых функций), количества узлов и шаги сетки, изменение нумерации столбцов и строк, уравнения узловых значений переменных и узловые значения краевых функций показаны на рисунке 2.

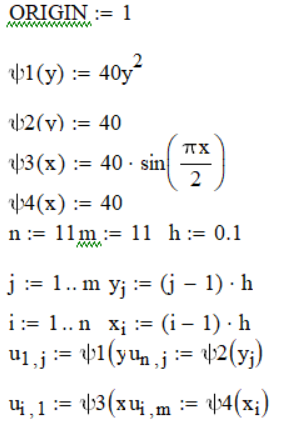
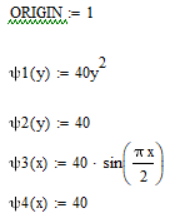
Рисунок 2 Задание исходных данных

Полученные значения показаны на рисунке 3.

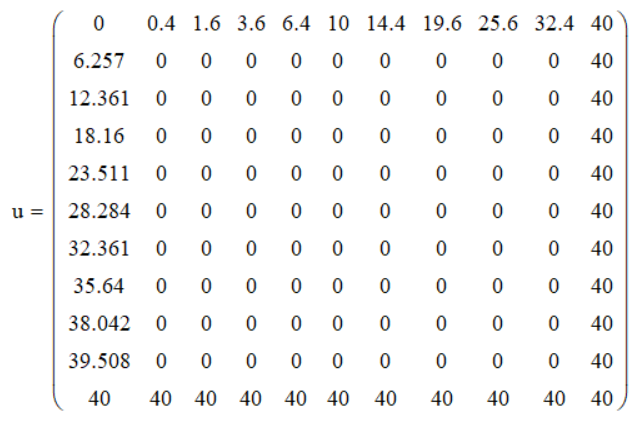
Рисунок 3 Краевые элементы матрицы

Система уравнений решается методом простых итераций, а начальное приближение показано на рисунке 4.

Рисунок 4 Матрица начального приближения функции

Программа для вычисления уравнения показана на рисунке 5.

Рисунок 5 Вычисление по методу простых итераций в MathCAD

Результат вычислений показан на рисунке 6.

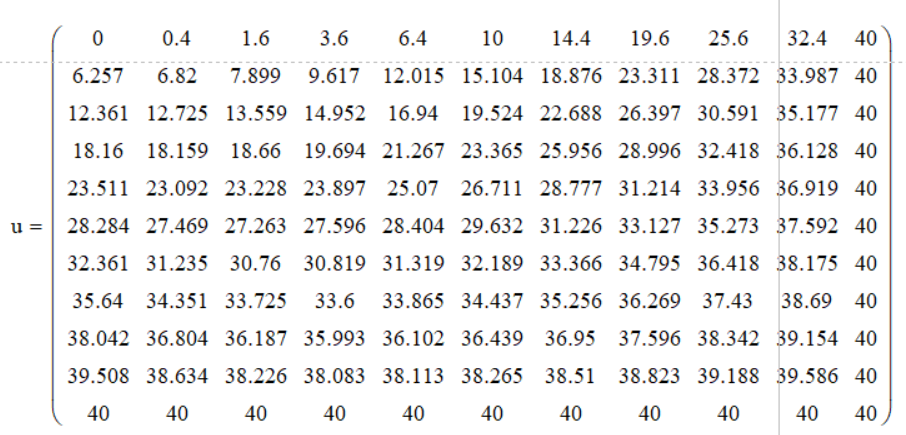
Рисунок 6 Результат выполнения программы метода простых итераций

Итоговый график показан на рисунке 8.

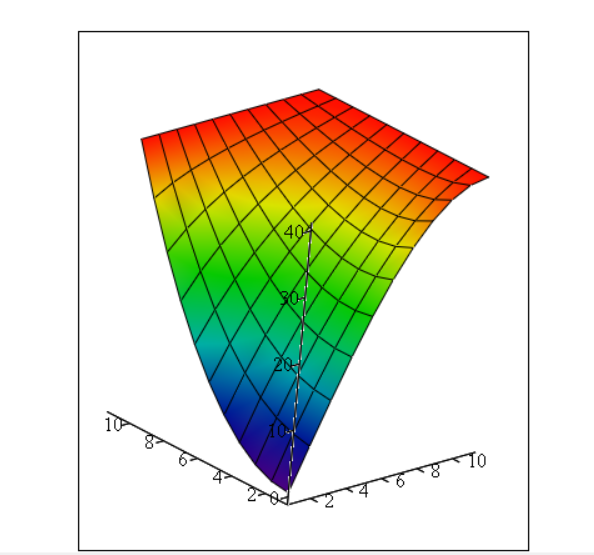
Рисунок 7 Результат решения задачи Дирихле для уравнения Лапласа

Вывод: в результате работы было найдено приближенное решение уравнения в заданной области с данными граничными условиями, неизвестная функция была представлена графиком поверхности.