4 сем / лаба8 вар8

Санкт-Петербургский Политехнический университет Петра Великого

Институт машиностроения, материалов и транспорта

Высшая школа машиностроения

ОТЧЕТ

по лабораторной работе № 8

Дисциплина: Вычислительная математика

Тема: Решение краевой задачи

(Вариант 8)

Студент группы 3331505/10001 Гричачина А.А.

Преподаватель Кожанова Ю.В.

Санкт-Петербург

2023 г.

Задание

Методами конечных разностей и прогонки найти решение краевой задачи на отрезке 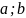(значения 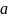и 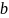указаны в краевых условиях) с шагом 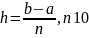(число промежутков).

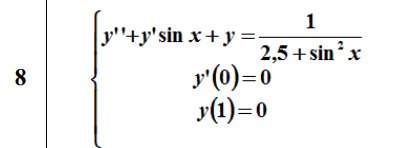
Рисунок 1 Задание восьмого варианта

Целью работы является закрепление знаний, полученных в лекционном

курсе «Вычислительная математика» по разделу «Решение краевых задач», приобретение навыков использования соответствующих численных методов с

применением программных средств автоматизации вычислений.

Краткие теоретические сведенья

Краевая задача – задача о нахождении решения заданного дифференциального уравнения, удовлетворяющего краевым (граничным) условиям на концах промежутка или на границе области.

Краевая задача для дифференциального уравнения второго порядка записывается в виде:

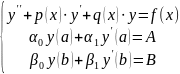
Здесь: p(x),q(x), f (x) - известные и непрерывные на функции, - заданные постоянные, ( ).

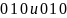Решение методом конечных разностей

Задание исходных данных (границы отрезка, количество интервалов и шага интегрирования) показаны на рисунке 2.

Рисунок 2 Задание исходных данных

Вычисление коэффициентов системы уравнений методом конечных разностей показано на рисунке 3.

Рисунок 3 Вычисление коэффициентов

Матрица правой части и вектор левой части системы уравнений показаны на рисунке 4.

Рисунок 4 Матрицы полученные методом конечных разностей

Программа для решения уравнения и график решений методом конечных разностей показаны на рисунке 5.

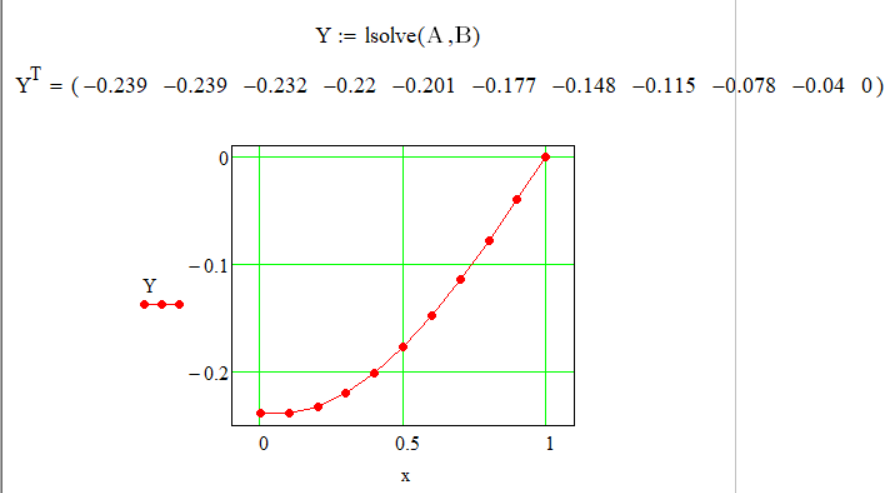
Рисунок 5 Метод конечных разностей, полученный в MathCAD

Решение методом прогонки

Задание исходных данных для метода подгонки такое же, как на рисунке 2 для метода конечных разностей.

Вычисление коэффициентов системы уравнений методом подгонки показано на рисунке 6.

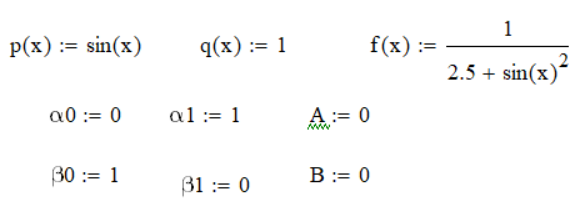
Рисунок 6 Вычисление коэффициентов

Прямой ход

Вычисление 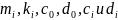показано на рисунке 7.

Рисунок 7 Задание прямого хода

Обратный ход

Вычисление 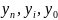и полученное решение с графиком показано на рисунке 8.

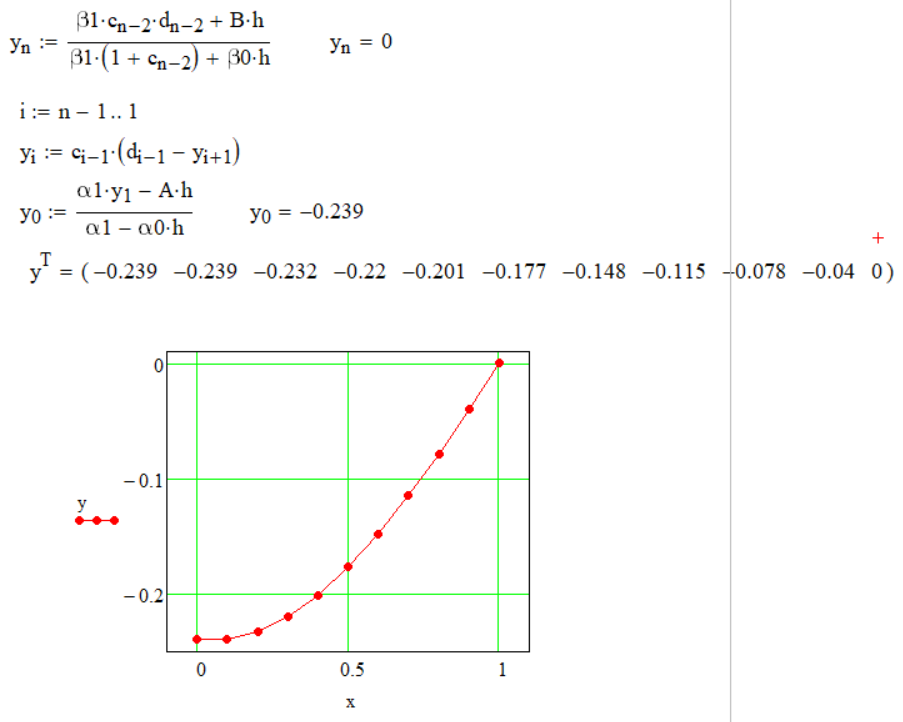
Рисунок 8 Метод подгонки, полученный в MathCAD

Вывод: в результате работы была найдена неизвестная функция различными способами на заданном интервале изменения независимой переменной x с данными начальными условиями.