4 сем / лаба7 вар18

Санкт-Петербургский Политехнический университет Петра Великого

Институт машиностроения, материалов и транспорта

Высшая школа машиностроения

ОТЧЕТ

по лабораторной работе № 7

Дисциплина: Вычислительная математика

Тема: Решение ОДУ второго порядка методами Эйлера и

Рунге-Кутты

(Вариант 18)

Студент группы 3331505/10001 Гричачина А.А.

Преподаватель Кожанова Ю.В.

Санкт-Петербург

2023 г.

Задание

Решить ОДУ второго порядка на промежутке a;b , разбив его на 10 интервалов:

1. Методами Эйлера и сравнить с точным решением. Для каждого метода найти требуемое количество интервалов разбиения промежутка для обеспечения относительной погрешности решения на конце промежутка не более . Для каждого метода проделать вручную первые три шага интегрирования.

2. Методом Рунге-Кутты и сравнить с точным решением.

3. С помощью встроенных функций MathCAD и сравнить с точным решением.

Вариант	ОДУ	Начальные условия	Точное решение	a	b
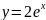
1				0	1

Рисунок 1 Задание первого варианта

Цель работы: изучить решение задачи Коши для ОДУ второго порядка численными методами Эйлера и Рунге-Кутты, а также встроенными функциями MathCAD и MATLAB.

Краткие теоретические сведенья

В общем виде ОДУ n – го порядка содержит независимую переменную, неизвестную функцию и ее производные (или дифференциалы) до n – го порядка включительно. ОДУ n – го порядка, разрешенное относительно старшей производной, может быть записано в виде:

Для корректной постановки задачи Коши требуется задать n начальных условий на саму функцию yx и ее производные от первого до n 1 порядка включительно, т.е. в виде:

Для решения ОДУ n – го порядка численными методами оно должно быть записано в виде системы ОДУ первого порядка.

Решение ОДУ методом Эйлера, подбор требуемого числа промежутков. Ручной расчет первых трех шагов интегрирования. Решение ОДУ методом Рунге-Кутты. Решение ОДУ встроенными функциями MathCAD.

Задание исходных данных (границы отрезка, количество интервалов и шага интегрирования) а так же точного решения показаны на рисунке 2.

Рисунок 2 Задание исходных данных и функций

Программа для решения системы ОДУ первого порядка методом Эйлера в MathCaD показана на рисунке 3.

Рисунок 3 Метод Эйлера в MathCAD

Совмещенный график точного и полученного решений и вычисление относительной погрешности показаны на рисунке 4.

Рисунок 4 Погрешность и сравнительный график метода Эйлера

Программа для решения системы ОДУ первого порядка методом рунге-Кутты показано на рисунке 5.

Рисунок 5 Метод Рунге-Кутты в MathCAD

Решение ОДУ первого порядка и совмещенный график точного и полученного решений показан на рисунке 6.

Рисунок 6 Решение и график методом Рунге-Кутты

Решение с помощью встроенной функцией MathCAD Given/Odesolve и сравнительный график показаны на рисунке 7.

Рисунок 7 Решение функцией Given/Odesolve

Решение с помощью встроенной функцией MathCAD rkfixed и сравнительным график показаны на рисунке 8.

Рисунок 8 Решение функцией rkfixed

Вывод: в результате работы была найдена неизвестная функция различными способами на заданном интервале изменения независимой переменной x с начальными условиями.