4 сем / лаба6 вар1

Санкт-Петербургский Политехнический университет Петра Великого

Институт машиностроения, материалов и транспорта

Высшая школа машиностроения

ОТЧЕТ

по лабораторной работе № 6

Дисциплина: Вычислительная математика

Тема: Решение ОДУ первого порядка методами Эйлера и

Рунге-Кутты

(Вариант 1)

Студент группы 3331505/10001 Гричачина А.А.

Преподаватель Кожанова Ю.В.

Санкт-Петербург

2023 г.

Задание

Решить ОДУ первого порядка на промежутке a;b , разбив его на 10 интервалов:

1. Методами Эйлера и сравнить с точным решением. Для каждого метода найти требуемое количество интервалов разбиения промежутка для обеспечения относительной погрешности решения на конце промежутка не более dop. Для каждого метода проделать вручную первые три шага интегрирования.

2. Методом Рунге-Кутты и сравнить с точным решением. Найти относительную погрешность на конце промежутка. При заданном шаге по методу Рунге найти оценку ошибки решения.

3. С помощью встроенных функций MathCAD.

Рисунок 1 Задание первого варианта

Цель работы: изучить численные методы Эйлера и Рунге-Кутты для решения задачи Коши для ОДУ первого порядка. Сравнить полученные приближенные решения с точными решениями и исследовать погрешности получаемых решений на конце промежутка.

Краткие теоретические сведенья

Обыкновенное дифференциальное уравнение первого порядка - уравнение относительно неизвестной функции одного аргумента, содержащее первую производную от этой функции по аргументу, и разрешенное относительно первой производной от неизвестной функции. В общем виде ОДУ первого порядка может быть записано так: . Решить (или проинтегрировать) дифференциальное уравнение — значит определить неизвестную функцию на заданном интервале изменения независимой переменной x.

Общий случай метода Эйлера для i-ой точки:

Первый модифицированный метод Эйлера:

Второй модифицированный метод Эйлера:

Метод Рунге-Кутты:

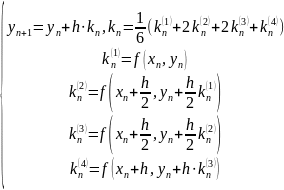
Решение заданного ОДУ методом Эйлера, 1-м и 2-м модифицированными методами Эйлера, совмещенные графики полученных решений и точного решения, нахождение числа промежутков для достижения требуемой точности.

Задание исходных данных (границы отрезка, произвольное количество интервалов и шага интегрирования) и функций правой части уравнения и точного решения показаны на рисунке 2.

Рисунок 2 Задание исходных данных и функций

Метод Эйлера в MathCaD, вычисление погрешности, а также совмещенный график точного и полученного решений показан на рисунке 3.

Рисунок 3 Метод Эйлера в MathCAD

Первый модифицированный метод Эйлера, вычисление погрешности и график точного и полученного решения показан на рисунке 4.

Рисунок 4 Первый модифицированный метод Эйлера в MathCAD

Второй модифицированный метод Эйлера, вычисление погрешности и график точного и полученного решения показан на рисунке 5.

Рисунок 5 Второй модифицированный метод Эйлера в MathCAD

Решение заданного ОДУ методом Рунге-Кутты, совмещенный график полученного решения и точного решения. Расчет ошибки интегрирования по методу Рунге.

Метод Рунге-Кутты и график точного и полученного решения показан на рисунке 6.

Вычисление относительной погрешности на конце промежутка и оценка ошибки решения по методу Рунге при заданном шаге показаны на рисунке 7.

Решение ОДУ встроенными функциями.

Вычислительный блок Given/Odesolve со сравнительным графиком функций, как и использование встроенной функции rkfixed с соответствующим графиком показано на рисунке 8.

Рисунок 6 Метод Рунге-Кутта в MathCAD

Рисунок 7 Погрешность и ошибка решения метода Рунге-Кутта

Рисунок 8 Решение ОДУ с помощью встроенных функций Given/Odesolve (слева) и rkfixed (справа)

Вывод: в результате работы была найдена неизвестная функция на заданном интервале изменения независимой переменной x различными способами. Метод Эйлера имеет наибольшую погрешность, поэтому пришлось взять 80 шагов, когда для первый модифицированного способа потребовалось всего 15 шагов, а для второго – 10. Наименьшую погрешность имеет метод Рунге-Кутта и использование встроенных функций MathCAD. Так же встроенные функции занимают меньше строк задания поиска необходимой функции.