4 сем / лаба5 вар1

Санкт-Петербургский Политехнический университет Петра Великого

Институт машиностроения, материалов и транспорта

Высшая школа машиностроения

ОТЧЕТ

по лабораторной работе № 5

Дисциплина: Вычислительная математика

Тема: Численное дифференцирование функций

(Вариант 1)

Студент группы 3331505/10001 Гричачина А.А.

Преподаватель Кожанова Ю.В.

Санкт-Петербург

2023 г.

Задание

Найти приближенные значения производных первого и второго порядка от заданной функции 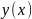на промежутке 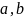с шагом 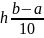в Excel и MathCAD и сравнить их с точными значениями.

Рисунок 1 Задание первого варианта

Целью работы является закрепление знаний, полученных в лекционном курсе «Вычислительная математика» по разделу «Численное дифференцирование», приобретение навыков использования соответствующих численных методов с применением программных средств автоматизации вычислений.

Теоретические сведенья

Численное дифференцирование — совокупность методов приближённого вычисления значения производной некоторой функции, заданной таблично или имеющей сложное аналитическое выражение.

Приближенное значение с использованием первой конечной разности:

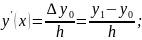
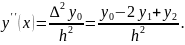
Приближенное значение с использованием трехточечной схемы:

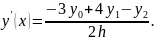
Результаты расчетов в Excel в форме таблиц и графиков

Использую формулы из теоретических сведений рассчитаем конечные разности и затем приближенное значение первой и второй производной (рис. 2,3,4). Две диаграммы сравнения с точными значениями показаны на рисунке 5.

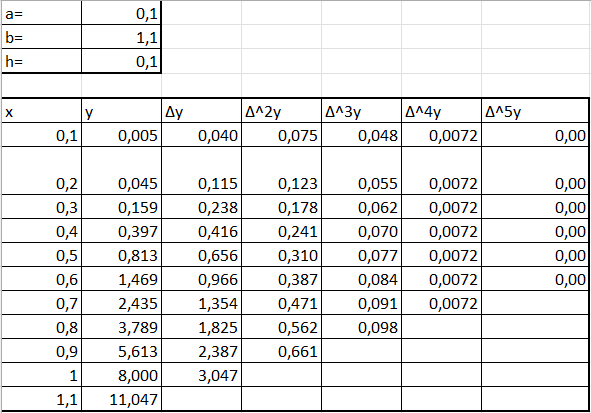
Рисунок 2 Расчет конечных разностей

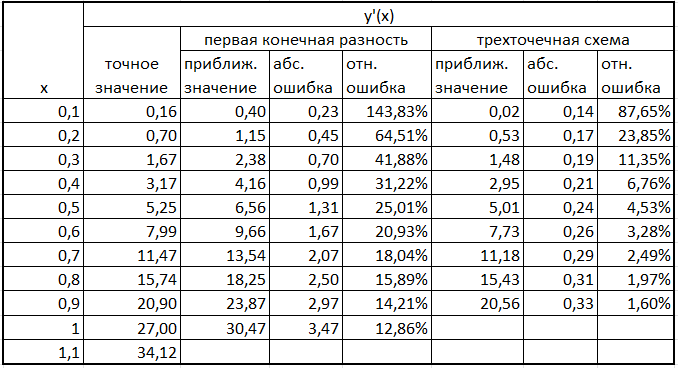
Рисунок 3 Определение погрешностей вычисления первой производной

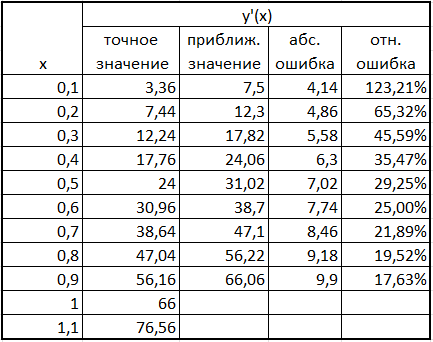
Рисунок 4 Определение погрешностей вычисления второй производной

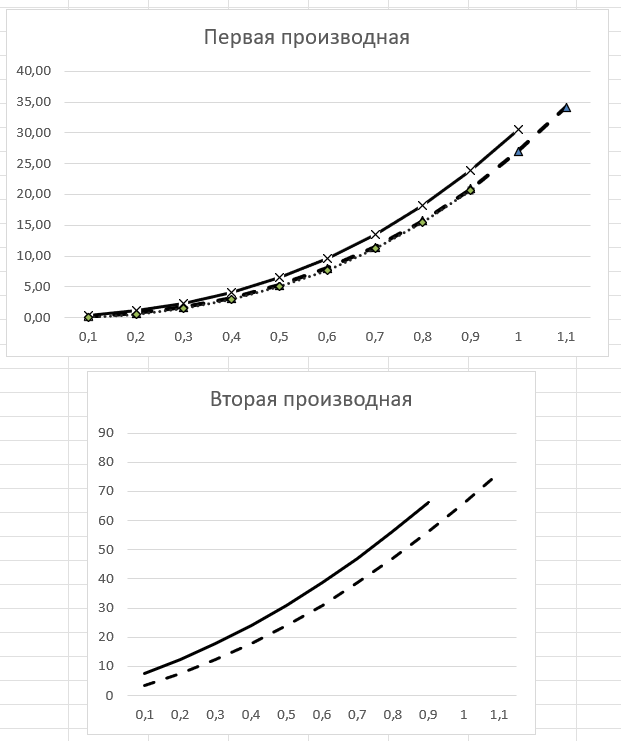
Рисунок 5 Графики точных и приближенных значений производных

Результаты расчетов в Mathcad

В MathCAD были забиты начальные данные для расчета из задания, вычислены производные. Затем вычислены узловые значения и первая производная с помощью первой конечной разности и по трехточечной схеме. Вычисление второй производной было произведено с помощью конечной разности второго порядка. Все записи в MathCAD показаны на рисунке 6.

Рисунок 6 Вычисления в MathCAD

Были созданы сравнительные графики для первой и второй производной (рис. 7 и 8).

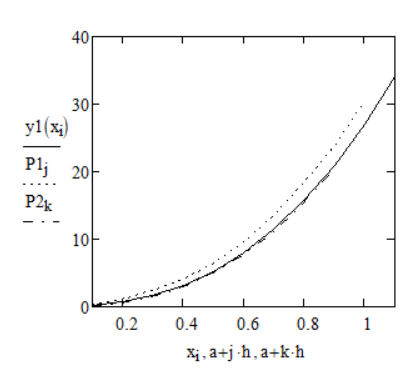
Рисунок 7 Сравнительный график для первой производной

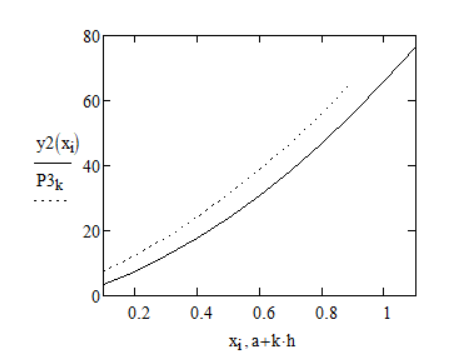
Рисунок 8 Сравнительный график для второй производной

Вывод: В результате работы были подсчитаны приближенные значения производных. Начальные значения приближенной функции имеют большую относительную и маленькую абсолютную ошибки, но по мере увеличения x относительная ошибка уменьшается, а абсолютная ошибка увеличивается.