
3 сем / РЗ 4 вар 1 / Титульный лист
.docxСанкт-Петербургский Политехнический университет Петра Великого
Институт машиностроения, материалов и транспорта
Высшая школа машиностроения
ОТЧЕТ
по лабораторной работе № 4
Дисциплина: Вычислительная математика
Тема: Приближенные методы решения алгебраических и
трансцендентных уравнений
(Вариант 1)
Студент группы 3331505/10001 Гричачина А.А.
Преподаватель Кожанова Ю.В.
Санкт-Петербург
2022 г.
Задание
Решить систему уравнений методом Гаусса и методом Зейделя.
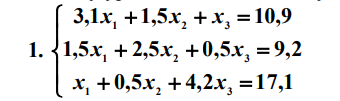
Рисунок 1 Задание первого варианта
Целью работы является изучение численных методов решения систем линейных уравнений. В настоящей работе рассматривается метод Гаусса и итерационный метод решения систем уравнений.
Теоретические сведенья
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
Метод Зейделя представляет собой некоторую модификацию метода итераций. Основная его идея заключается в том, что при вычислении (k + 1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k + 1)-е приближения неизвестных x1, x2, …, xi - 1.
Выполненные задания
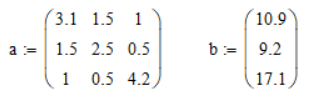
Рисунок 2 Программа, реализующая алгоритм решения системы уравнений методом Гаусса

Рисунок 3 Программа, реализующая алгоритм решения системы уравнений методом Гаусса

Рисунок 4 Программа, реализующая метод Зейделя

Рисунок 5 Нахождение корней двумя методами
Вывод: Методом Зейделя решать короче, чем методом Гаусса, но получают приближенное значение корней, а в методе Гаусса являются точным способом.
