3 сем / РЗ 3 вар 9 / Титульный лист

Санкт-Петербургский Политехнический университет Петра Великого

Институт машиностроения, материалов и транспорта

Высшая школа машиностроения

ОТЧЕТ

по лабораторной работе № 3

Дисциплина: Вычислительная математика

Тема: Приближенные методы решения алгебраических и

трансцендентных уравнений

(Вариант 9)

Студент группы 3331505/10001 Гричачина А.А.

Преподаватель Кожанова Ю.В.

Санкт-Петербург

2022 г.

Задание

Найти все корни уравнения с точностью до пяти знаков после запятой. Для одного из корней проделать ручные расчеты трех шагов приближений по всем методам.

Методы нахождения корней:

• Метод деления отрезка пополам.

• Метод хорд.

• Метод касательных (методом Ньютона).

• Метод итераций.

Найти также все корни уравнения с помощью встроенной функции MathCAD root.

Таблица 1 Заданная функция

Функция

Целью работы является изучение численных методов решения алгебраических и трансцендентных уравнений.

Теоретические сведенья

Метод деления отрезка пополам: дана функция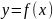 непрерывная на отрезке 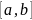и удовлетворяющая условию 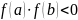. Точка 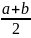разбивает начальный отрезок на два: 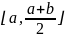и .

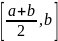Отрезок, на концах которого функция имеет одинаковые знаки, отбрасываем, как не содержащий корень. Оставшийся отрезок обозначим 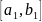. Длина этого отрезка равна 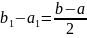. На k -м шаге деления отрезка пополам его длина будет равна:

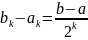
Процесс деления отрезка пополам прекращается при условии: 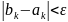, где 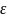– требуемая точность вычисления корня уравнения.

Метод хорд: дана функция непрерывная на отрезке и удовлетворяющая условию . Очередное приближение 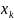корня уравнения 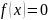в методе хорд вычисляется по формуле:

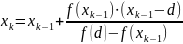
где 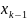– предыдущее приближение корня, – неподвижная граница отрезка.

В качестве начального приближения 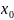принимается одна из границ отрезка, удовлетворяющая условию:

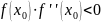
где 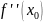– значение второй производной функции в точках

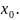
Противоположная граница будет неподвижной (точка d). Вычисления корня прекращаются при условии, что: .

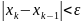Метод касательных (метод Нютона): дана функция и ее первкая производная 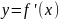, непрерывные на отрезке . Функция удовлетворяет условию . Очередное приближение корня уравнения в методе касательных вычисляется по формуле:

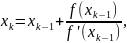
где - предыдущее приближение корня.

В качестве начального приближения принимается одна из границ отрезка, удовлетворяющая условию:

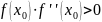
Вычисления корня прекращаются при условии, что:

Метод итерации: Требуется найти корень уравнения , который расположен внутри промежутка [a,b]. Исходное уравнение преобразуется к виду:

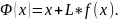
Тогда

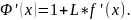
Множитель L выбирается таким, чтобы 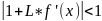, что гарантирует сходимость итерационного процесса к корню уравнения.

Использование встроенной функции Mathcad root: Уравнение должно быть записано в виде 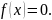Встроенная функция root может быть:

• root (f(x), x) – где x требует задания начального значения, вблизи этого числа будет поиск корня;

• root (f(x),x,a,b), где a,b - границы интервала, внутри которого происходит поиск корня.

Выполненные задания

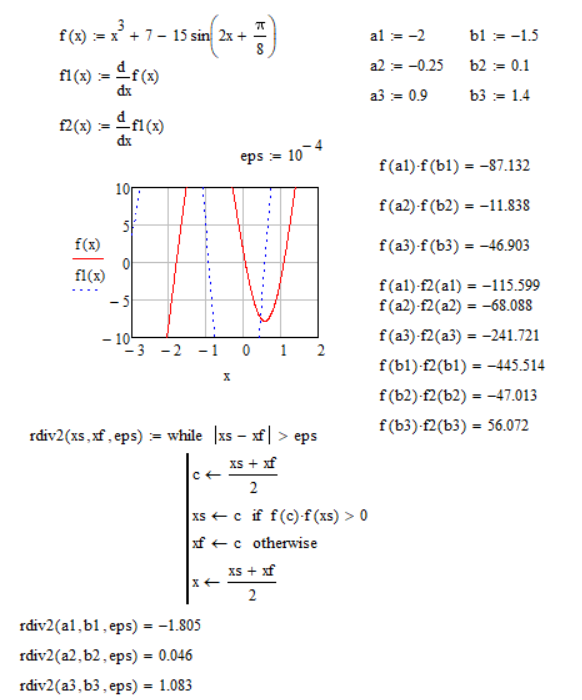
Рисунок 1 Ввод данных, нахождение корней уравнения методом деления отрезка пополам

Рисунок 2 Нахождение корней уравнения методом хорд и касательных

+

Рисунок 3 Нахождение корней методом итерации

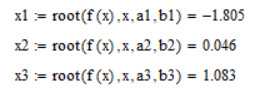
Рисунок 4 Нахождение корней уравнения с помощью встроенной функции MatCAD root

Ручные расчеты трех шагов приближений по всем методам для одного из корней:

Вывод: Для всех методов нахождения корней уравнения необходимы выполнения условия непрерывности функции на промежутке и удовлетворяющая условию . Метод деления отрезка пополам является наиболее простым для понимания и подсчета. Метод хорд чуть сложнее по подсчету и требует задания неподвижной границы отрезка по условию: . Метод касательных (методом Ньютона) так же требует задания начального приближения по условию . Все перечисленные методы прекращают вычисления при условии . Метод итераций требует преобразования уравнения с определенными условиями и не имеет возможности вычисления корня с определенной точностью.