Вопрос 21
Дифференциальное уравнение n -го порядка имеет вид:
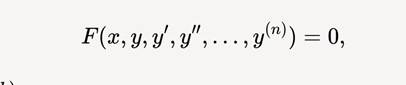
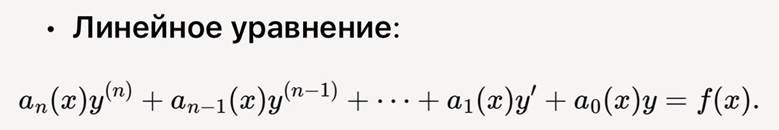
Если f(x) = 0 , уравнение называется однородным, иначе — неоднородным.
• Нелинейное уравнение: содержит нелинейные комбинации y и её производных (например, (y')^2 , y y'' ).
2. Уравнения, допускающие понижение порядка
Понижение порядка возможно, если структура уравнения позволяет ввести замену переменных, которая уменьшает порядок производных. Рассмотрим основные типы уравнений, допускающих понижение порядка.
2.1. Уравнения, не содержащие явно зависимую переменную y
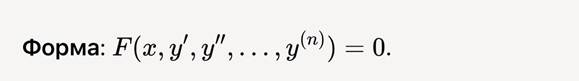
Метод понижения порядка:
• Вводим замену: y' = p , где p = p(x) . Тогда:
• y'' = p' ,
• y''' = p'' ,
• и так далее.
• Уравнение преобразуется в уравнение порядка n-1 для p(x) .
• После нахождения p(x) интегрируем y' = p(x) , чтобы найти y(x) .
2.2. Уравнения, не содержащие независимую переменную x
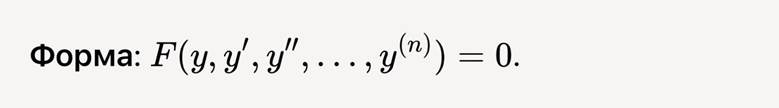
Метод понижения порядка:
• Вводим замену: y' = p , где p рассматривается как функция от y : p = p(y)
Тогда:
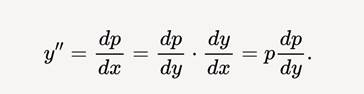
Вопрос 22
Общий вид:
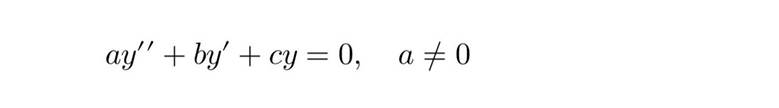
Составляем характеристическое уравнение:
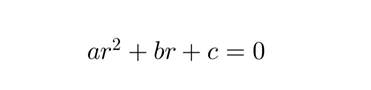
· Варианты корней и общее решение:
1. Два действительных различных корня r1 не равно r2
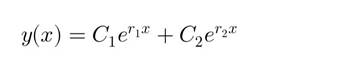
2. Два равных (действительных) корня r_1 = r_2 = r
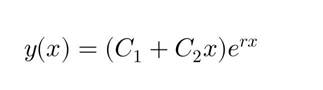
3.
Комплексные корни
![]()
Вопрос 23
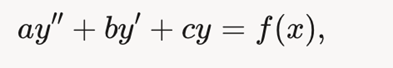
Общее решение:
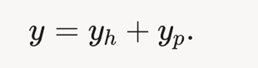
Yh – общее решение соответствующее однородному решению
Yp- частное решение неоднородного уравнения
Решение однородного уравнения:
![]()
Составляем характеристическое уравнение:
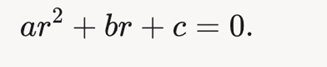

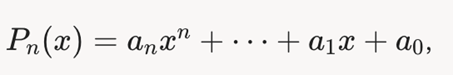
Частное решение для специальной правой части (метод неопределённых коэффициентов)
Метод неопределённых коэффициентов применяется, если правая часть f(x) имеет вид:
·
Полинома:

·
Экспоненты
![]()
· Тригонометрических функций:
![]()
·
Их комбинаций
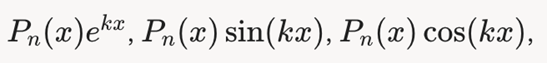

Вопрос 24
Общее решение:
Yh – общее решение соответствующее однородному решению
Yp- частное решение неоднородного уравнения
Решение однородного уравнения:
Составляем характеристическое уравнение:
Частное решение для специальной правой части (метод неопределённых коэффициентов)
Метод неопределённых коэффициентов применяется, если правая часть f(x) имеет вид:
· Полинома:
· Экспоненты
· Тригонометрических функций:
· Их комбинаций
Вопрос 25
1. Модели экономического роста
Дифференциальные уравнения используются для описания динамики капитала, производства и других макроэкономических показателей. Наиболее известной является модель Солоу.
· Модель Солоу: Рассмотрим базовую модель накопления капитала. Уравнение, описывающее изменение капитала K(t)):
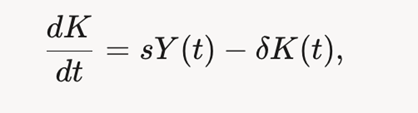

2. Динамика цен и рыночное равновесие
Дифференциальные уравнения моделируют, как цены изменяются во времени в ответ на спрос и предложение.
· Уравнение ценовой динамики: Предположим, что скорость изменения цены P(t) пропорциональна разнице между спросом D(P) и предложением S(P)
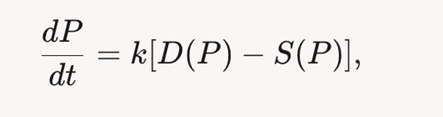
где k>0— коэффициент скорости адаптации.
3. Модели накопления капитала и инвестиций
Дифференциальные
уравнения описывают, как инвестиции
влияют на рост активов фирмы или
домохозяйства.: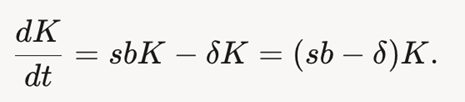
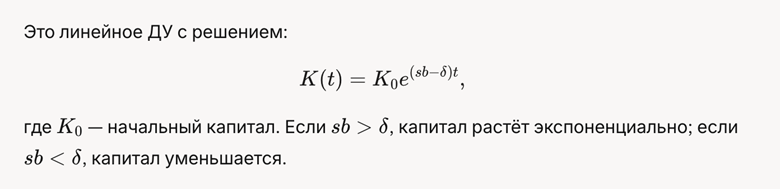
4. Модели поведения потребителей
Дифференциальные уравнения применяются для анализа динамики потребления и сбережений. Например, в модели Кейнса-Рамсея потребление домохозяйства оптимизируется с учётом межвременных предпочтений.
· Уравнение потребления: Уравнение Эйлера для оптимального потребления C(t)
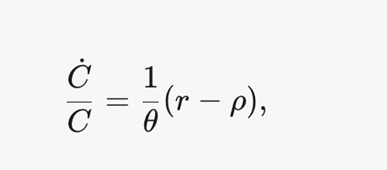

5. Модели инвентарного контроля
Дифференциальные уравнения используются для управления запасами на складах. Например, если запасы S(t) уменьшаются со скоростью, пропорциональной спросу D(t) и пополняются с постоянной скоростью R:
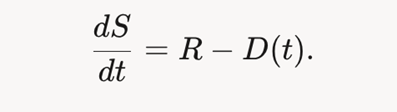
6. Эконометрика и вероятностные модели
Дифференциальные уравнения применяются для моделирования случайных процессов, например, в моделях цен акций (модель Блэка-Шоулза) или в анализе временных рядов.
·
Пример: Модель Блэка-Шоулза: Цена
опциона V(S,t) удовлетворяет уравнению: