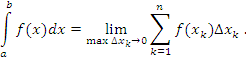Вопрос 8
Пусть на [a;b] задана непрерывная неотрицательная функция y = f (x).
Определение 1. Криволинейной трапецией называется фигура, ограниченная осью абсцисс прямыми x = a, x = b и графиком функции y = f(x).
Ставится задача: вычислить площадь этой криволинейной трапеции
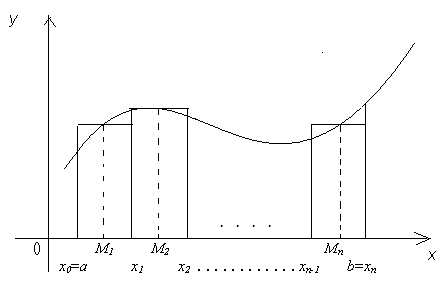
1) Разобьем отрезок [a;b] на n частей точками x0 = a; x1; x2; xn-1; xn = b и проведем прямые x = x1, x = x2, … x = xт-1, которые разобьют трапецию на n частей.
2) Обозначим xk = xk - xk-1 – длины отрезков разбиения [a;b]. На каждом их отрезков произвольно выберем точку Mk (k = 1;… n).
Построим на каждом из отрезков прямоугольники с высотами, равными значению функции в выбранных точках Mk .
Площади полученных прямоугольников равны: S1 = f (M1) D x1; S2 = f (M2) D x2; ….; Sn = f (Mn) D xn .
3) Найдем сумму этих площадей:
Получили
площадь ступенчатой фигуры. Эта площадь
зависит от способа разбиения отрезка
[a;b] на части и от выбора на каждой из
частей точек Mk (k = 1;… n).
Чем
больше будет точек разбиения [a;b] на
части и мельче по длине эти части, тем
точнее сумма
будет приближаться к площади данной
криволинейной трапеции. То есть можно
записать:
Определение
2. Сумма
называется интегральной суммой функции
f (x) на отрезке [a;b].
Определение 3. Предел интегральной суммы S функции f (x) на [a;b] при n и max D xk 0 называется определенным интегралом функции f (x) на отрезке [a;b], если этот предел существует и не зависит ни от способа разбиения [a;b] на части, ни от выбора точек Mk (k = 1;… n) на каждой из частей. Следовательно, можно записать:
.
При этом отрезок [a;b] называют отрезком интегрирования, “a” – нижним пределом интегрирования, “b” – верхним пределом.
Вопрос 9
Если
существует предел интегральной суммы
(1), который не зависит от способа разбиения
интервала [a,b] и выбора точек
,
то этот предел называется определенным
интегралом от функции f(x) по промежутку
[a,b] и обозначается символическим
выражением
|
|
(2) |
|
Заметим,
что если
,
то все
и
.
При стремлении
к нулю каждое слагаемое суммы (2) стремится
к нулю, но при этом число слагаемых
стремится к бесконечности. Результатом
этих двух взаимно противоположных
стремлений является некое число,
называемое определенным интегралом.
Величины a и b называются соответственно нижним и верхним пределами интегрирования, а процедура вычисления интеграла (2) называется интегрированием.
Обозначение
интеграла в виде
введено Лейбницем, где f(x)dx напоминает
о слагаемое суммы
,
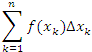а символ ∫ представляет собой
стилизованную начальную букву латинского
слова "Summa".
Если
на промежутке [a,b], то интегральная сумма
стремится к площади криволинейной
трапеции и, таким образом, интеграл
равен площади области, ограниченной
графиком функции y = f(x) и осью 0x от x =
a до x = b.
Пусть F(x) - первообразная функции f(x) :
Тогда
при
,
где
- изменение функции F(x) на промежутке
.
Следовательно,
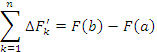
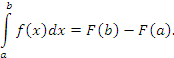
Формула играет ключевую роль в интегральном исчислении и называется формулой Ньютона-Лейбница
Свойства определенного интеграла
1.
Если функция f(x) непрерывна на отрезке
[a;b], то постоянный множитель можно
выносить за знак интеграла:
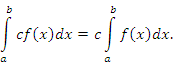
2.
Если функции f(x) и g(x) непрерывны на
отрезке [a;b], то интеграл от алгебраической
суммы интегрируемых функций равен
алгебраической сумме интегралов:
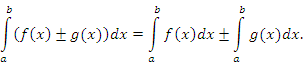
3. Если функция f(x) непрерывна на наибольшем из отрезков [a;b], [a;c] и [c;b], то при любом расположении точек a, b и c на оси Х верно неравенство:
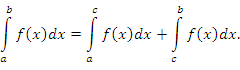
4.
Теорема о среднем. Если функция f(x)
непрерывна на отрезке [a, b], то на этом
отрезке существует точка
такая, что
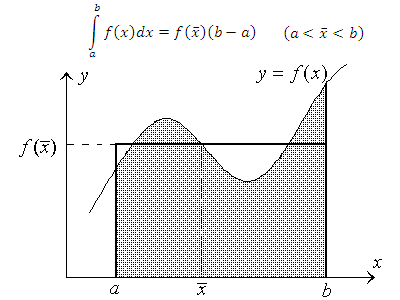
5. Если функция f(x) ≥0 на отрезке [a;b], a<b, и интегрируема на этом промежутке, то
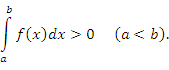
6. Если функции f(x) и g(x) непрерывны на отрезке [a;b], a<b, и f(x) ≥ g(x) при любом X ∊ [a;b], то
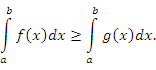
7.
Если функция f(x) непрерывна на отрезке
[a, b], a<b и для любого X ∊ [a;b] справедливо
неравенство
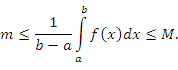
8. Если функция непрерывна на отрезке [a, b], то
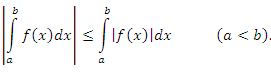
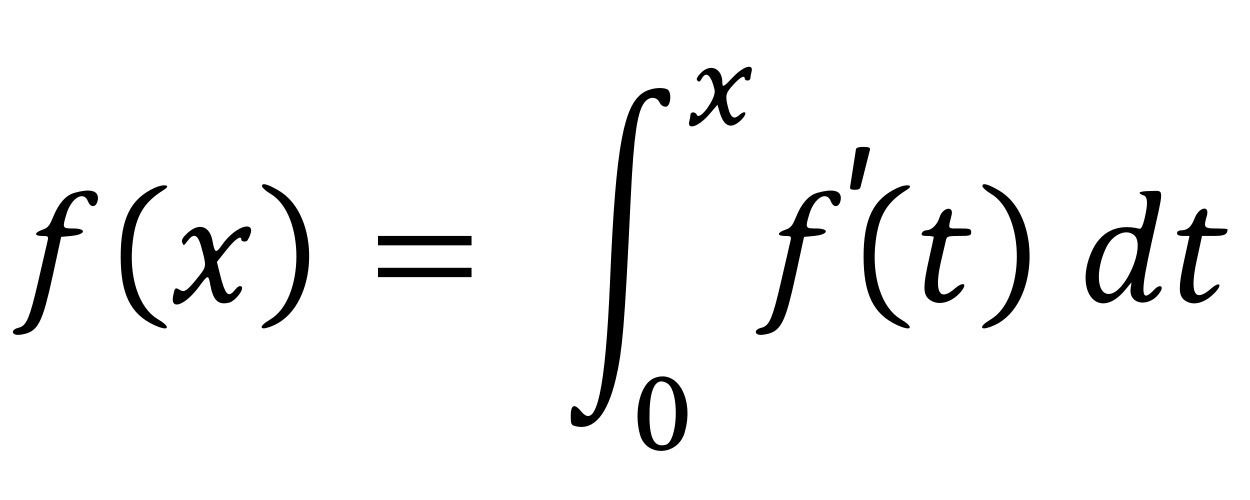
9. Если функция f(x) непрерывна на отрезке [a, b], то