Вопрос 5
Некоторые часто встречающиеся интегралы от иррациональных функций можно вычислить методом рационализации подынтегральной функции. Этот метод заключается в отыскании такой подстановки, которая преобразует интеграл от иррациональной функции в интеграл от функции рациональной. Можно выделить следующие типы интегралов от иррациональных функций:
1.
. Для таких интегралов рационализация
достигается подстановкой
, гдеm – общий знаменатель рациональных
чисел Р1, Р2,…, Pn.
2.
Интегралы типа
сводятся
к табличным после выделения под радикалами
полного квадрата и последующей
подстановкой
.
3.
Интегралы типа
приводятся
к рационально зависящим от тригонометрических
функций выражениям с помощью следующих
тригонометрических подстановок
соответственно: х=asint или x=acost, x=atgt,
.
Пример 1
Найти
неопределенный интеграл
прямая
замена
.
При этом
,
где
. В результате подстановки
– корень пропадает. если
,
то
.
Навешиваем
дифференциалы на обе части:
Т.е.
Проведём
замену
,
следовательно:
(1)
Проводим подстановку после замены (как,
что и куда, уже рассмотрено).
(2)
Выносим константу за пределы интеграла.
Числитель и знаменатель сокращаем на
.
(3) Получившийся интеграл является табличным, готовим его для интегрирования, выделяя квадрат
(4)
Интегрируем по таблице, используя
формулу
.
(5)
Проводим обратную замену. Если
,
то
.
Вопрос 6
Интегрирование некоторых тригонометрических функций осуществляется комбинацией методов разложения и замены переменной. Рассматриваются следующие функции:
1. Четные степени синуса и косинуса, Интегралы от них находят, применяя формулу понижения степени
2. Нечетные степени синуса и косинуса. Интегралы от них вычисляют, отделяя от нечетной степени множитель в первой степени и подводя его под знак дифференциала
3. Произведения sin^m(x)cos^n(x). Они интегрируются так же, как и в случае 1, если m и n оба четные, и так же,как в случае 2, если m или n нечетно.
4. Частные sin^m(x)/cos^n(x) и cos^n(x)/sin^m(x). Они интегрируются так же, как в случае 2 если m нечетно
5. Произведения sinmx cosnx, sinmx • sinnx и cosmx cosnx. Их интегрируют, преобразуя подынтегральное выражение с помощью формул
Вопрос 7
Интегрирование иррациональных выражений, вообще говоря, представляет большую трудность. Многие интегралы от иррациональных функций не выражаются через элементарные функции. Поэтому мы рассмотрим только некоторые частные случаи, когда заменой переменных можно от интеграла от иррациональной функции перейти к интегрированию рациональных выражений.
1.Рассмотрим интеграл вида
где R– рациональная функция,m, n, … p,q– целые числа
Пусть
к- общий знаменатель дробей
.
Применим
подстановку
Тогда каждая дробная степень выразится через целую степень tи иррациональная функция преобразуется в рациональную
Например
Применим
подстановку
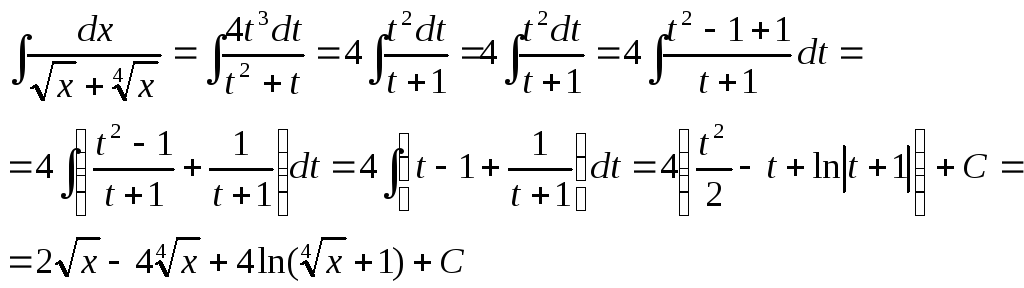
2.Интегралы вида
вычисляются с помощью подстановки
гдеk-
наименьшее общее кратное чиселn…q
Эта подстановка сведет интеграл от иррациональной функции к интегралу от рациональной дроби.
Например:
Обозначим
тогда
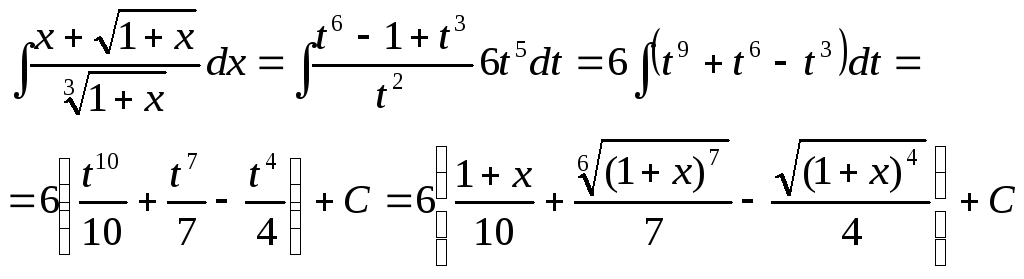
Интегрирование тригонометрических функций
Пусть
требуется найти
интеграл
вида
Применим
подстановку
тогда
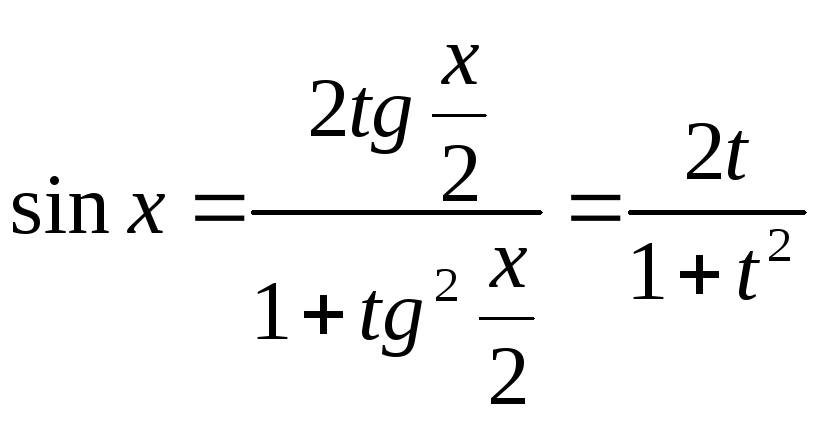
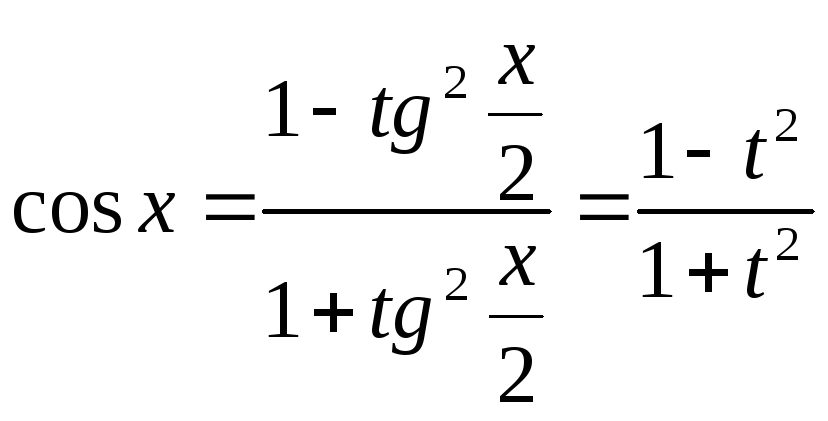
Далее найдем
Подстановка , носит названиеуниверсальной тригонометрическойподстановки; она сводит вычисление интеграла от тригонометрических функций к интегрированию рациональных выражений.
Например:
Обозначим
тогда
Тогда
