1. Определение неопределённого интеграла, его свойства, геометрический смысл. Таблица неопределённых интегралов.

2. Методы нахождения неопределённых интегралов. Непосредственное интегрирование. Метод замены переменной.

3. Интегрирование неопределённых интегралов по частям.

4. Интегрирование рациональных дробей. Разложение на простые дроби.

5. Интегрирование иррациональных функций.

6. Интегрирование тригонометрических функций.

7. Интегрирование некоторых иррациональных функций.

8. Задачи, приводящие к понятию определённого интеграла.

9. Определение определённого интеграла. Свойства определённого интеграла.

10. Теорема о производной интеграла с переменным верхнем пределом. Формула Ньютона- Лейбница.

11. Вычисление площадей плоских фигур с помощью определённого интеграла.

12. Вычисление объёмов тел вращения с помощью определённого интеграла. Вычисление длины дуги графика функции с помощью определённого интеграла.

13. Несобственные интегралы 1 рода, понятие об их сходимости, вычисление.

14. Несобственные интегралы 2 рода, понятие об их сходимости, вычисление.

15. Дифференциальные уравнения. Основные понятия.

16. Дифференциальные уравнения с разделяющимися переменными.

17. Однородные уравнения первого порядка.

18. Линейные дифференциальные уравнения первого порядка. Методы Лагранжа и И. Бернулли их решения.

19. Уравнение Бернулли, его решение.

20. Уравнение в полных дифференциалах.

21. Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка.

22. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение. Вид общего решения однородного уравнения.

23. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод Лагранжа вариации произвольных постоянных.

24. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами со специальной правой частью.

25. Экономические приложения интегралов.

26. Экономические приложения дифференциальных уравнений.

Вопрос 1

Множество всех первообразных для данной функции (х) на промежутке Х называется неопределенным интегралом от функции (х):

∫f(x)dx = F(x)+C F'(x) = f(x)

Слово «неопределенный» подчеркивает, что в общее выражение входит слагаемое, которое можно выбрать произвольным.

Примеры:

∫2xdx=x^2+C

∫cosxdx=sinx+C

∫e^xdx=e^x+C

Пять свойств неопределенного интеграла

Свойство 1. Производная от неопределенного интеграла

Производная от неопределенного интеграла подынтегральной функции: равна

(∫f(x)dx)' = f(x)

Свойство 2. Дифференциал неопределенного интеграла

Дифференциал неопределенного интеграла равен

подынтегральному выражению:

d(∫f(x)dx) = f(x)d(x)

Свойство 3. Неопределенный интеграл от дифференциала

Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого С.

∫dF(x)=F(x)+C

Свойство 4. Вынесение постоянного множителя за знак интеграла

Постоянный множитель можно выносить за знак интеграла

∫kf(x)dx=k∫ f(x)dx

Свойство 5. Интеграл от алгебраической суммы двух функций

Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:

∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx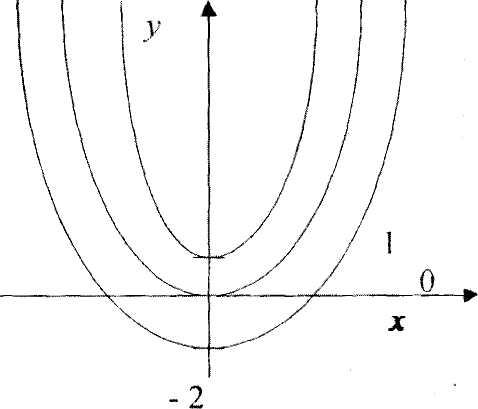

Неопределенный интеграл ∫f(x)dx представляет собой семейство кривых у = F(x) + С, каждая из которых может быть получена путём параллельного переноса другой вдоль оси OY. Эти кривые называются интегральными кривыми. Все кривые данного семейства обладают общим свойством: если провести касательные в точках с одинаковой абсциссой х = х0, то эти касательные будут параллельны. Действительно, их угловые коэффициенты равны

[F(x) + С]'=F'(x) │=f(x0).

Таблица:

∫x^n dx = x^{n+1}/(n+1) + C, (n ≠ -1)

∫1/x dx = ln|x| + C

∫e^x dx = e^x + C

∫a^x dx = a^x/ln(a) + C

∫sin(x) dx = -cos(x) + C

∫cos(x) dx = sin(x) + C

∫1/(1 + x^2) dx = arctg(x) + C

∫1/√(1 - x^2) dx = arcsin(x) + C

Вопрос 2

В этом случае, чтобы найти неопределенный интеграл, нужно с помощью определенных приемов свести его к табличному виду и дальше воспользоваться таблицей интегралов. Рассмотрим два из возможных методов вычисления неопределенных интегралов.

I. Непосредственное интегрирование.

Здесь достаточно элементарных алгебраических преобразований подинтегральной функции для того, чтобы получить табличный интеграл.

Непосредственное интегрирование основано на применении свойств интеграла и (или) таблицы интегралов.

Проиллюстрируем этот метод решением конкретных примеров:

1)

Для вычисления этого интеграла воспользуемся формулами (4), (5), (6) и формулой № 2 таблицы 1, тогда

= = =

2) , т.к. известно, что sin 2x = 2 sin x cos x, то

(см. формулу (6) и № 6 табл.1)

Пример от Карасева:

∫(5x²-6x² - 2)dx = ∫5x+dx- ∫6x2dx - ∫2dx = x^5-2x^3-2x+C

∫[(1+sinx)dx = ∫dx + ∫sin xdx = x - cosx+C

II. Метод замены переменной (метод подстановки).

Метод основан на понятии производной сложной функции F(φ(x))

Теорема Если функция f(t) имеет F(t), а функция t=φ(x) дифференцируема, то функция также имеет первообразную

∫f(φ(x))d(φ(x))=F(φ(x))+C

В этом методе определенную часть подинтегрального выражения обозначают новой переменной. Всю последовательность действий, приводящих к решению, рассмотрим на примерах.

1. Надо вычислить интеграл .

Для того, чтобы получить ответ:

а) введем новую переменную t = 3x;

б) найдем ее дифференциал: dt = 3dx;

в) выразим dx через dt: dx = dt/3;

г) подставим новые значения в исходный интеграл: , используя формулу(6) получим: , это табличный интеграл;

д) по формуле №7 табл. или, возвращаясь к старой переменной, .

Правильность ответа легко проверить, вычислив от него производную, при правильном решении она должна быть равна подинтегральной функции: