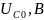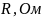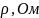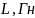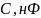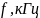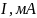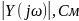- •Обработка результатов
- •7.2.1 Исследование резонанса напряжений и ачх контура с малыми потерями
- •7.2.2 Исследование резонанса напряжений и ачх контура с большими потерями
- •7.2.3 Исследование влияния емкости на характеристики контура
- •7.3.1 Исследование резонанса токов и ачх контура с малыми потерями
- •7.3.2 Исследование резонанса токов и ачх контура с большими потерями
- •7.3.3 Исследование влияния изменения емкости на характеристики контура
Цель работы: исследование резонанса и АЧХ последовательного и параллельного колебательных контуров.
Резонанс – состояние RLC- цепи в установившемся синусоидальном режиме, при котором напряжение и ток на входе цепи совпадают по фазе.
Рис.1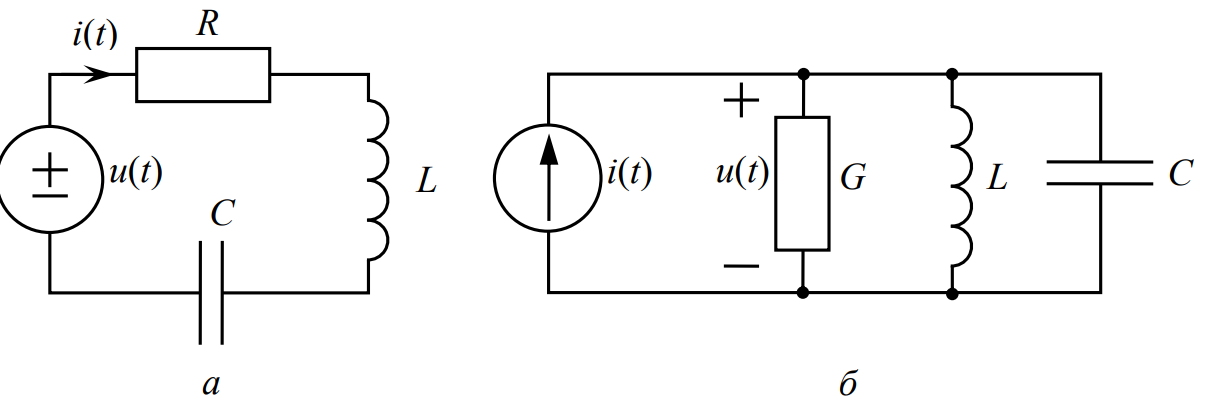

Резонансная частота приведенных на рис.1 а,б цепей:
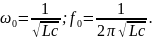
При резонансе модуль проводимости цепи на рис.1. а становится максимальным:
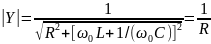
Это
значит, что при
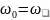 максимальным будет ток:
максимальным будет ток:
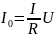
Отношение действующего значения
напряжения любого из реактивных элементов
к напряжению источника при
называют добротностью
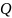 последовательного контура:
последовательного контура:
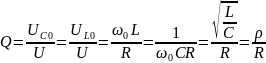
где
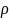 -
характеристическое сопротивление
контура.
-
характеристическое сопротивление
контура.
Если в режиме резонанса измерены
напряжения на входе и на конденсаторе,
ток
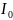 и резонансная частота
и резонансная частота
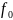 ,
то из приведенных соотношений можно
определить все параметры последовательного
контура:
,
то из приведенных соотношений можно
определить все параметры последовательного
контура:
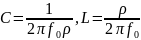
Параллельный RLC-контур на рис. 1, б дуален последовательному. При резонансе токов максимальным становится модуль его комплексного сопротивления:
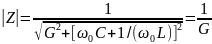
Это значит, что при максимальным будет напряжение на входе цепи:
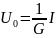
Отношение действующего значения тока любого из реактивных элементов к току источника при называют добротностью параллельного контура:
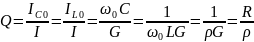
АЧХ последовательного контура есть зависимость модуля проводимости от частоты:
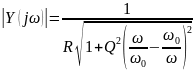
Для параллельного контура, дуально, АЧХ- это зависимость модуля сопротивления от частоты:
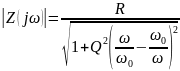
По
АЧХ можно определить добротность
контура. Она равна отношению
к полосе пропускания
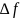 ,
измеренной по уровню 0,707 от максимума
АЧХ:
,
измеренной по уровню 0,707 от максимума
АЧХ:

Обработка результатов
7.2.1 Исследование резонанса напряжений и ачх контура с малыми потерями
Рис.2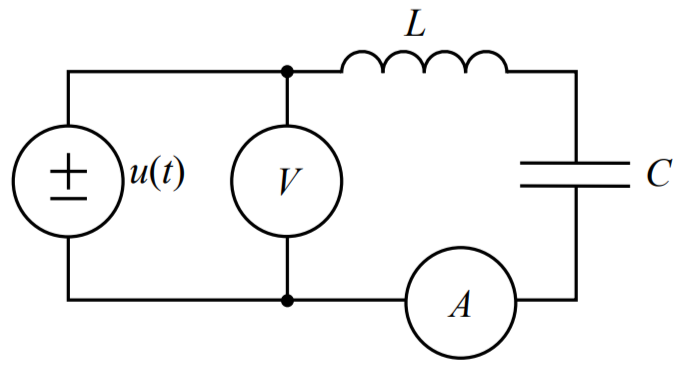

Изменяя частоту ГС, был определен резонансный ток. Результаты измерений приведены в таблице 1.
Таблица 1 – Результаты измерений и вычислений
Измерено |
Вычислено |
||||||||
|
|
|
|
|
|
|
|
|
|
2,04 |
13,40 |
4,75 |
39,40 |
152,24 |
19,31 |
2940,30 |
0,10 |
11,40 |
|
Определим
 по известным формулам:
по известным формулам:
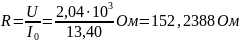
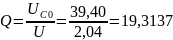
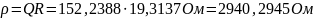
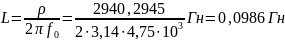
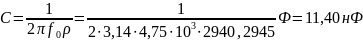
Экспериментальные точки АЧХ приведены в таблице 2
Таблица 2 – точки АЧХ и результат вычислений
Измерено |
Вычислено |
|
|
|
|
2,375 |
0,08 |
0,00004 |
3 |
0,71 |
0,000355 |
3,75 |
1,38 |
0,00069 |
4,5 |
12,38 |
0,00619 |
4,75 |
13,40 |
0,0067 |
5,25 |
2,26 |
0,00113 |
6 |
1,22 |
0,00061 |
6,75 |
0,74 |
0,00037 |
7,5 |
0,54 |
0,00027 |
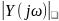 рассчитывается по формуле:
рассчитывается по формуле:
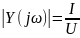
где
 .
.
Пример расчета:
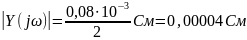 .
.
По
данным таблицы 2 построим АЧХ. На том же
графике изобразим АЧХ, определенное по
формуле:
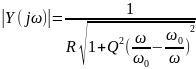
где
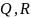 и
и
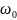 ,
определенные при резонансе остаются
постоянными на всех частотах
,
определенные при резонансе остаются
постоянными на всех частотах
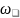 .
График изображен на рисунке 3.
.
График изображен на рисунке 3.
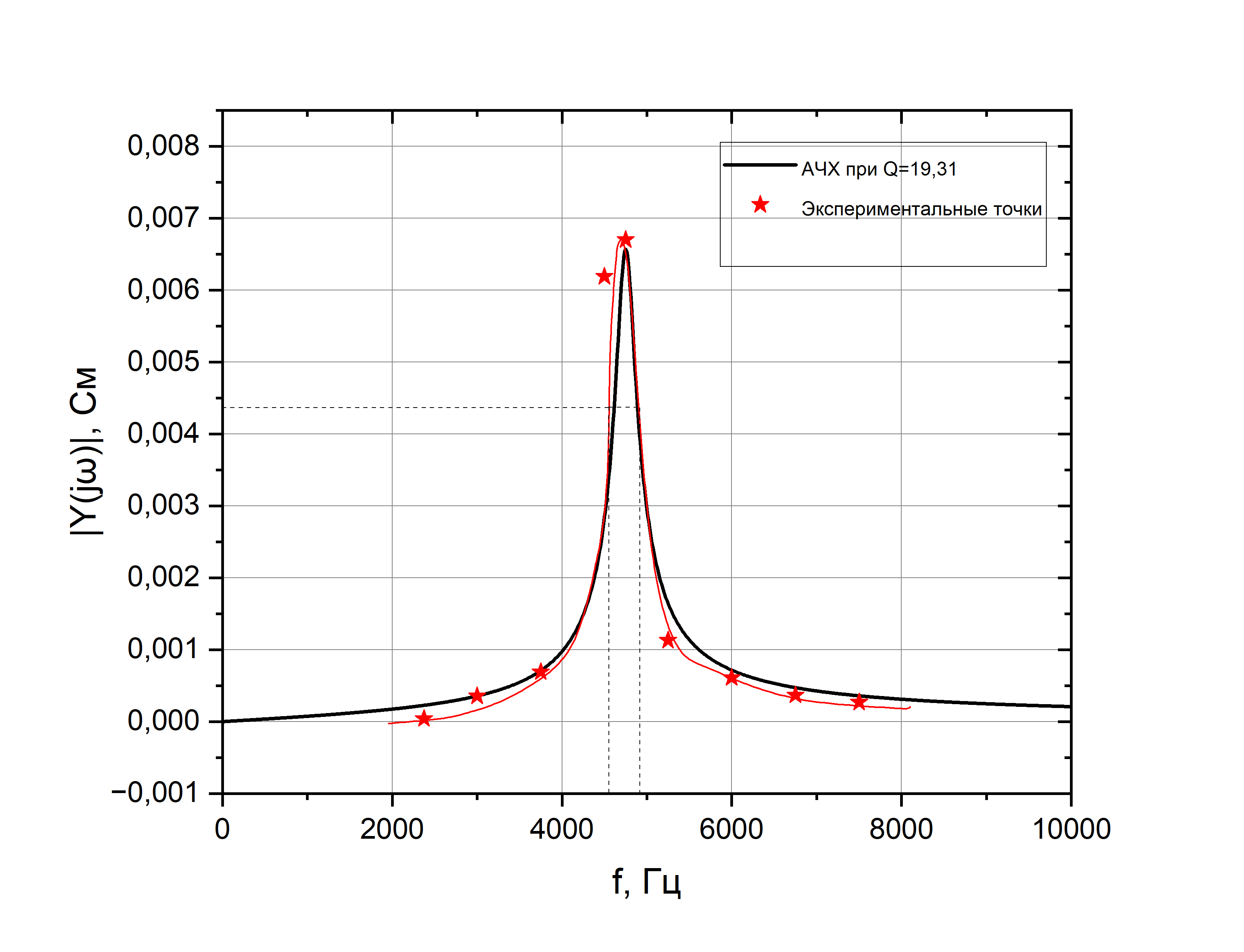
Рис.3 –АЧХ
Из-за высокой погрешности данных здесь и далее аппроксимация выполняется вручную с исключением аномальных точек.
Оценим добротность из графика:
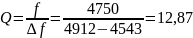
|
7.2.2 Исследование резонанса напряжений и ачх контура с большими потерями
Рис.4
– Схема
контура с большими потерями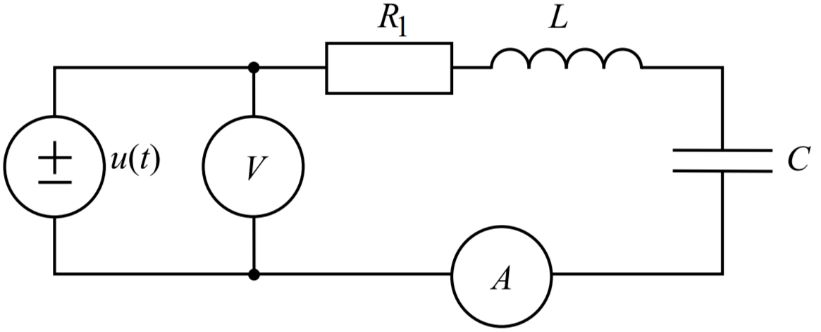

Все исследования проводились аналогично опыту 7.2.1.
Результаты поиска резонансного тока приведен в таблице 3. Все вычисления проводятся аналогично 7.2.1.
Таблица 3 – Результаты измерений и вычислений
Измерено |
Вычислено |
||||
|
|
кГц |
|
|
|
2,01 |
3,42 |
4,5 |
11,25 |
587,72 |
5,60 |
Экспериментальные точки АЧХ приведены в таблице 4.
Таблица 4 – точки АЧХ и результат вычислений
Измерено |
Вычислено |
|
|
|
|
1,5 |
0,089 |
0,000045 |
2,25 |
0,352 |
0,000176 |
3 |
0,745 |
0,000373 |
3,75 |
1,03 |
0,000515 |
4,5 |
3,42 |
0,00171 |
4,75 |
2,04 |
0,00102 |
6 |
1,02 |
0,00051 |
6,75 |
0,74 |
0,00037 |
7,5 |
0,54 |
0,00027 |
9 |
0,38 |
0,00019 |
По
данным таблицы 4 построим АЧХ, там же
изобразив АЧХ при
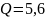 .
Результат на рисунке 5.
.
Результат на рисунке 5.
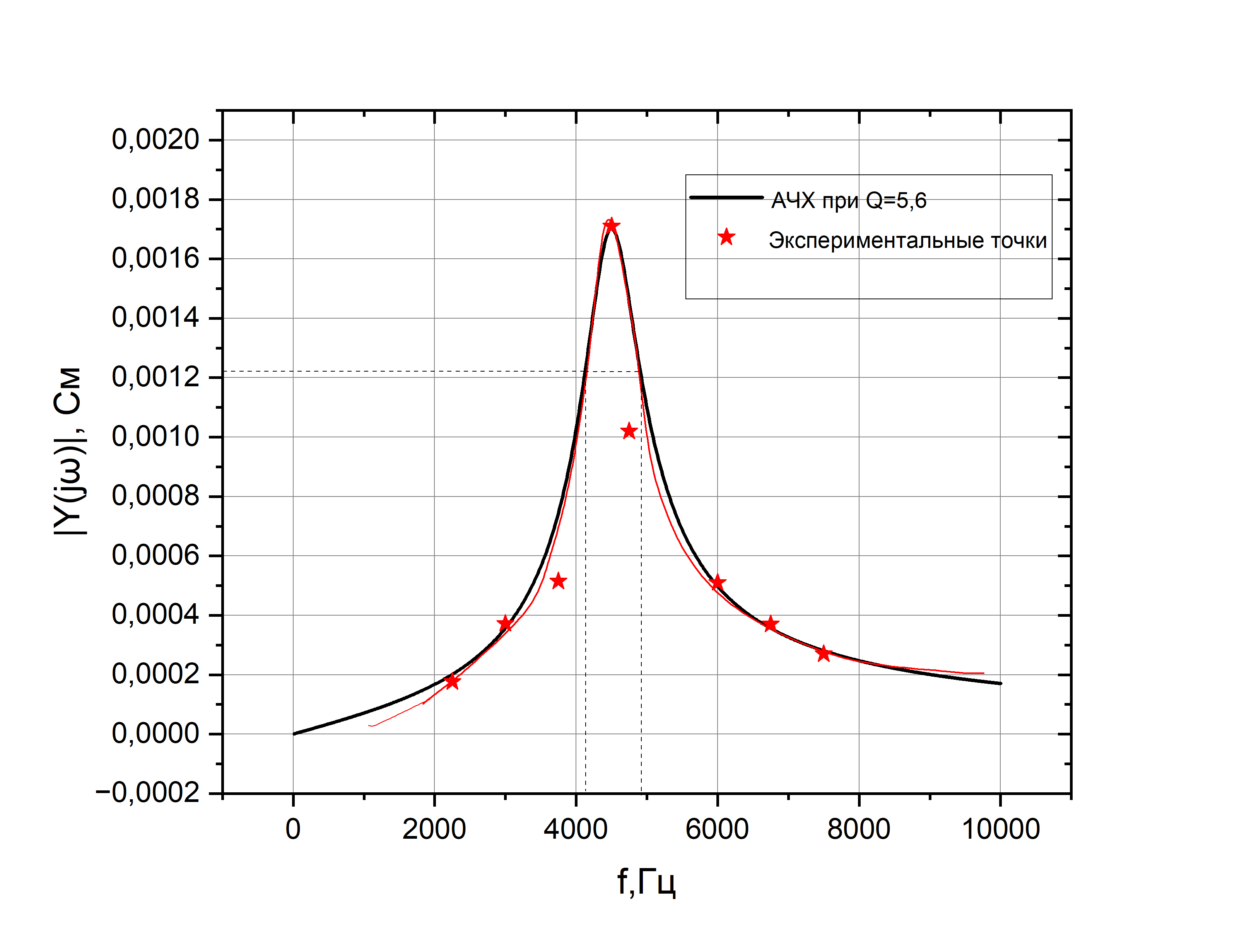
Рис.5- АЧХ
Оценим добротность из графика:
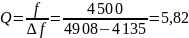

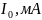
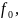 кГц
кГц