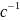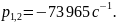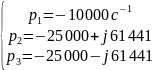лабы / ЛР3
.docxЦель работы: изучение связи между видом свободного процесса в электрической цепи и расположением её собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.
Общие сведения
В работе исследуются свободные процессы в цепях, схемы которых представлены на рис. 1. Цепи возбуждаются короткими импульсами тока i0(t), заряжающими конденсатор С. В паузах между импульсами конденсатор разряжается; цепь находится в свободном режиме, так как в это время источник возбуждения отключен (i0 = 0). Напряжения на элементах цепи осциллографируются.
Поведение линейных цепей описывается линейными дифференциальными уравнениями; при этом вид свободного процесса определяется корнями pk характеристического уравнения (собственными частотами цепи).
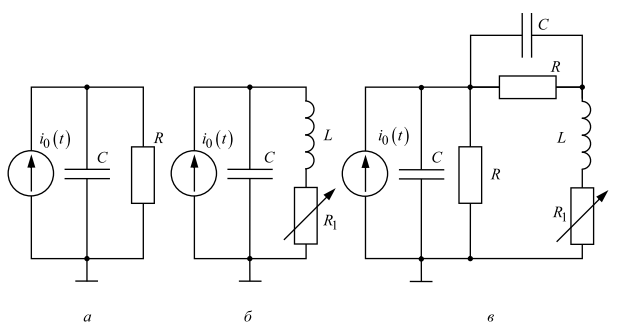
Рис. 1
При возбуждении цепи источником тока собственные частоты можно рассчитать как нули входной проводимости цепи Y(p), т. е. как корни уравнения Y(p) = 0.
Для цепи первого порядка, представленной на рис. 1, а, Y(p) = pC + 1/R, откуда
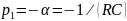 .
.
Для цепи второго порядка (на рис. 1, б) Y(p) = pC + 1/(pL + R1), откуда
![]()
Для цепи третьего порядка, представленной на рис. 3, в,

откуда
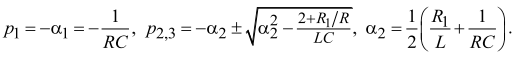
У цепи первого порядка одна собственная частота p1 – вещественная и отрицательная; свободный процесс описывается затухающей экспонентой:
![]()
где u – напряжение на каком-либо элементе цепи; t – время; α – постоянная затухания; τ – постоянная времени; A – постоянная интегрирования. Временная диаграмма свободного процесса приведена на рис. 2, а, причём τ – интервал времени, соответствующий любой подкасательной к экспоненте.
У цепи второго порядка две собственные частоты p1,2 могут быть вещественными (простыми или кратными) или комплексно-сопряжёнными.
В случае вещественных простых собственных частот
![]()
свободный процесс описывается суммой двух экспонент:
![]()
и называется апериодическим. Временная диаграмма процесса для случая A1 = –A2 и τ1 > τ2 приведена на рис. 2, б; штрихами показаны отдельные составляющие процесса.
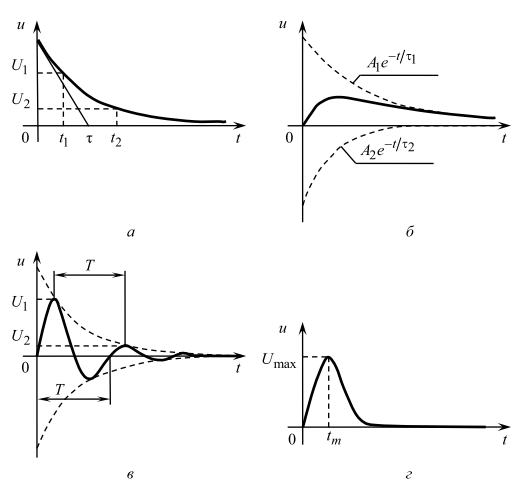
Рис. 2
Обработка результатов
3.2.1 Исследование свободных процессов в цепи первого порядка
В
эксперименте использовалась схема,
изображенная на рисунке 3. (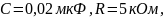 источником
тока
источником
тока
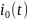 является генератор импульсов).
является генератор импульсов).
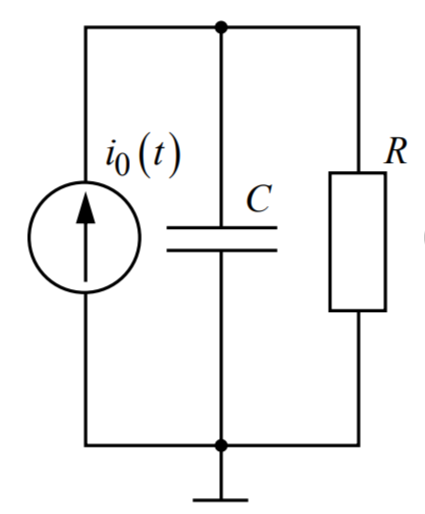
Рис. 3
Собственная частота цепи:
Рис.2
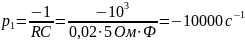 .
.
Рис.4.
– Осциллограмма свободного процесса



Значение
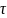 есть пересечение касательной с осью
X. Из рисунка видно, что
есть пересечение касательной с осью
X. Из рисунка видно, что
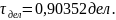 Учитывая, что
Учитывая, что
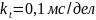 :
:
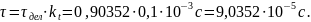
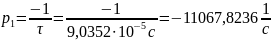
Рис.5. – Собственные частоты
свободного процесса в цепи первого
порядка

3.2.2 Исследование свободных процессов в цепи второго порядка
В опыте использовалась схема, изображенная
на рисунке 6. (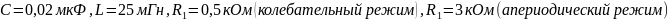 ).
).
Рис.7. – Осциллограмма
колебательного режима
Рис.6.



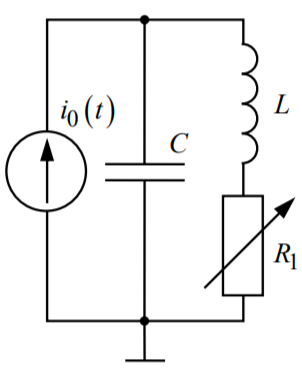 Осциллограмма
колебательного режима изображена на
рисунке 7.
Осциллограмма
колебательного режима изображена на
рисунке 7.
Определим собственные частоты по известным параметрам цепи:
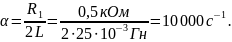
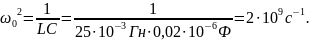
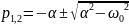
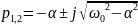
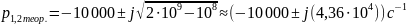
Найдем собственные частоты по осциллограмме (рис.7). Из графика (учтем, что ):
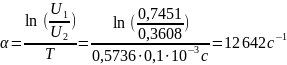
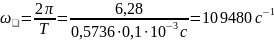
Тогда экспериментальные значения собственных частот:
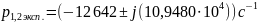
Рис.8. – Собственные частоты
колебательного режима
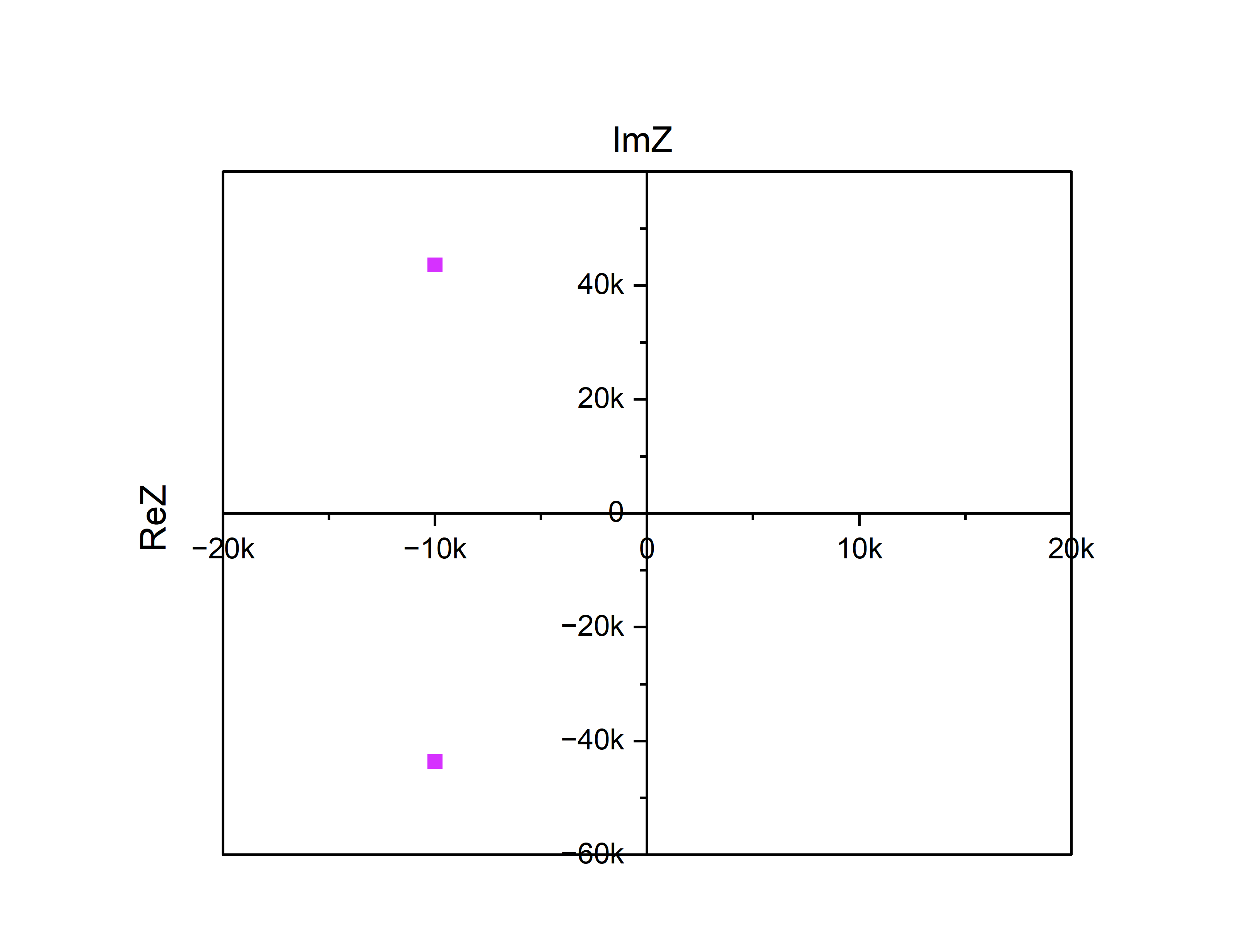 Собственные
частоты на комплексной плоскости
изображены на рис. 8. (только теоретические
значения).
Собственные
частоты на комплексной плоскости
изображены на рис. 8. (только теоретические
значения).
Рис.9. – Осциллограмма
апериодического режима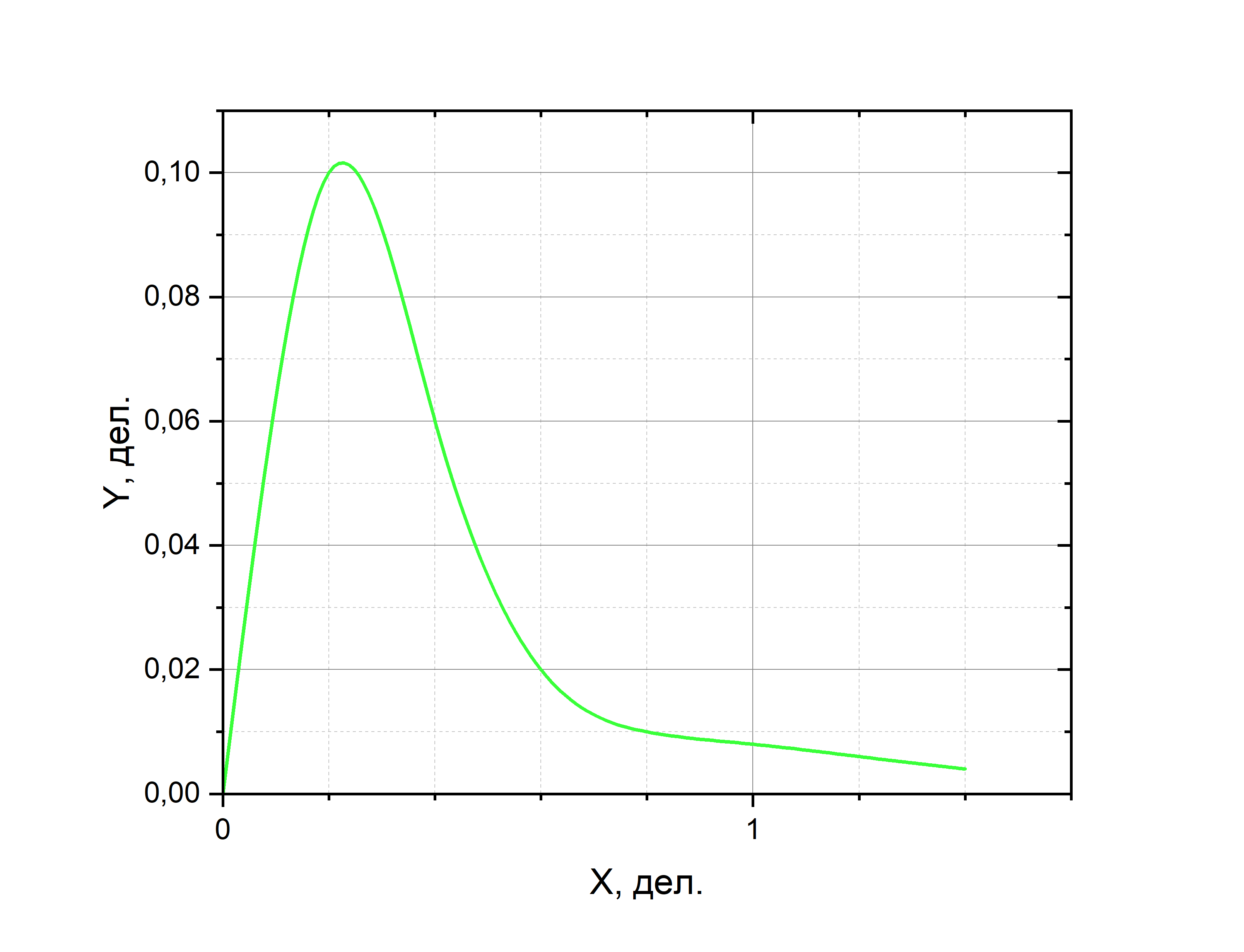

Определим собственные частоты из параметров цепи:
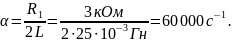
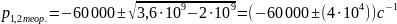
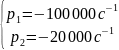
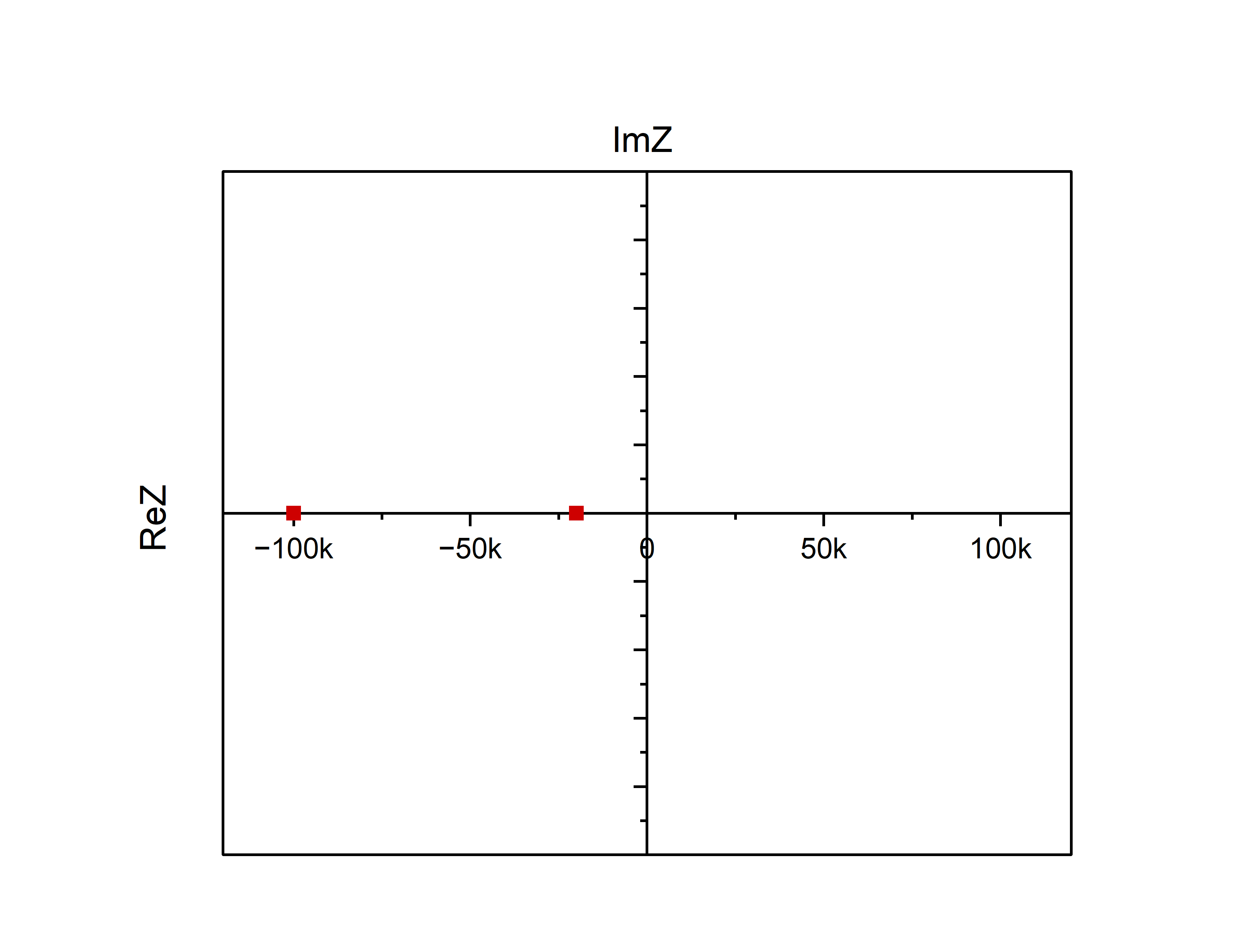
Рис.10. – Собственные частоты
апериодического режима
Рассмотрим критический режим. Осциллограмма изображена на рис.11.
Рис.11 – Осциллограмма
критического режима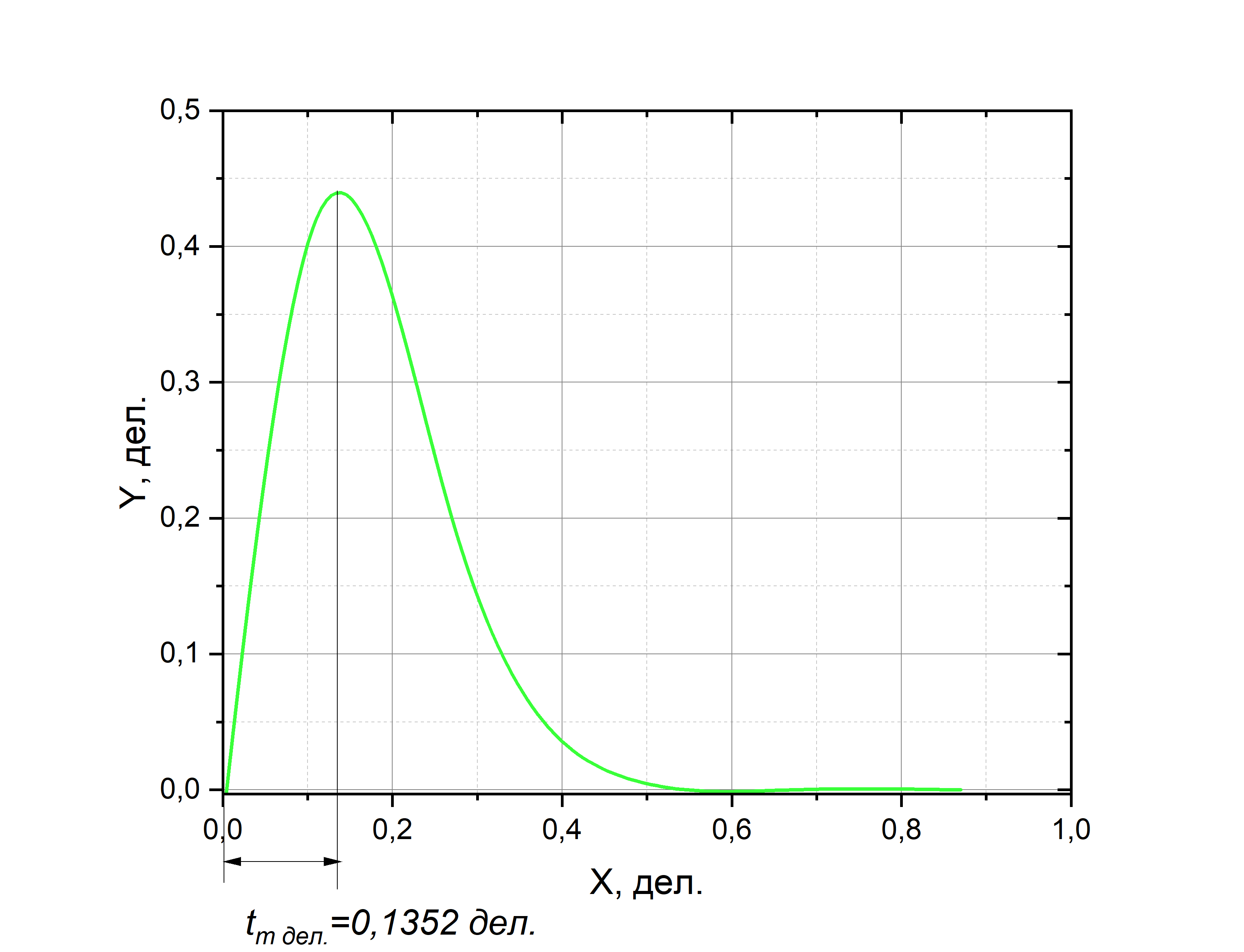

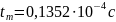 .
Собственные частоты:
.
Собственные частоты:
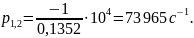
Рассчитаем собственные частоты, учитывая,
что
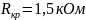 :
:
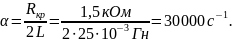
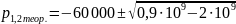
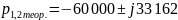
При теоретические собственные частоты содержат мнимую часть, что не соответствует опытным данным и критическому режиму.
Рис.12.
– Собственные частоты критического
режима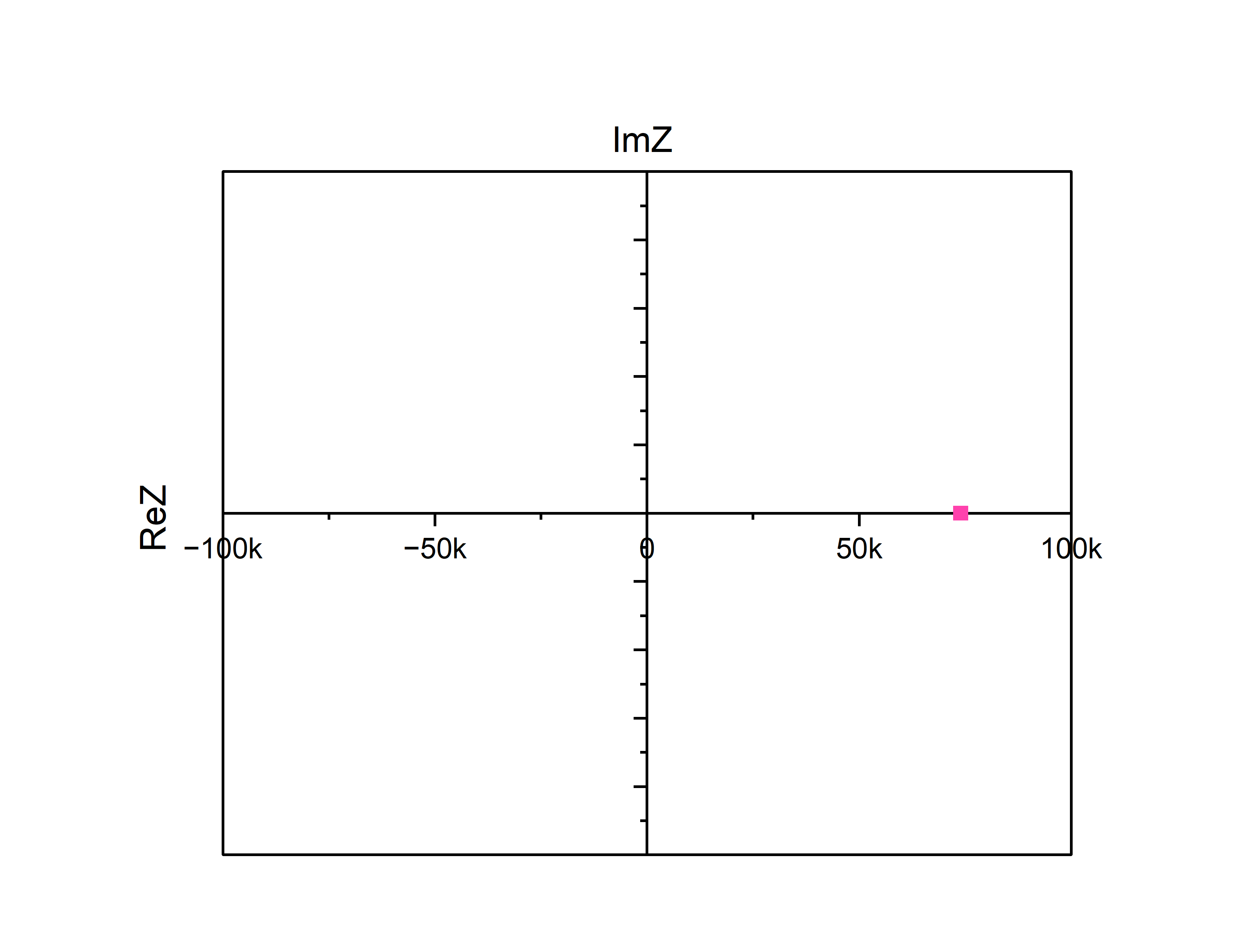

Рис. 13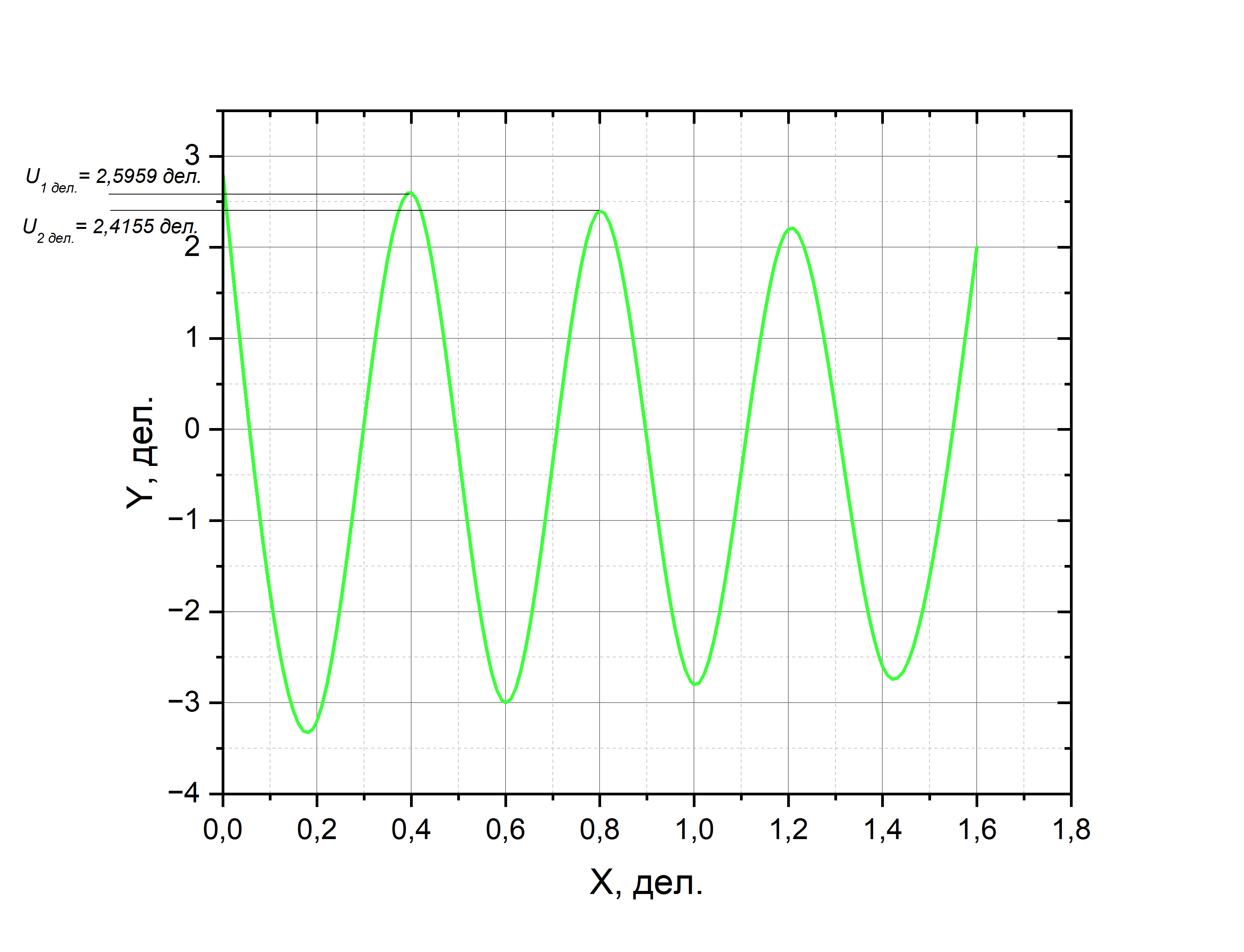

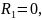 изображена
на рисунке 13.
изображена
на рисунке 13.
Определим
добротности контуров
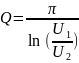 при
при
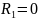 и
и
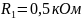 :
:
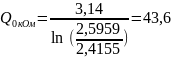
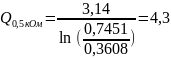
3.2.3 Исследование свободных процессов в цепи третьего порядка
В опыте была реализована схема,
изображенная на рисунке 14. ((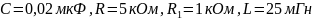 ).
Полученная осциллограмма напряжения
на входе цепи изображена на рисунке 15.
).
Полученная осциллограмма напряжения
на входе цепи изображена на рисунке 15.
Рис.14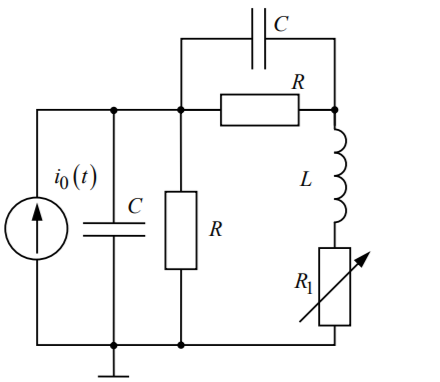

Рис.15. – Осциллограмма
напряжения на входе цепи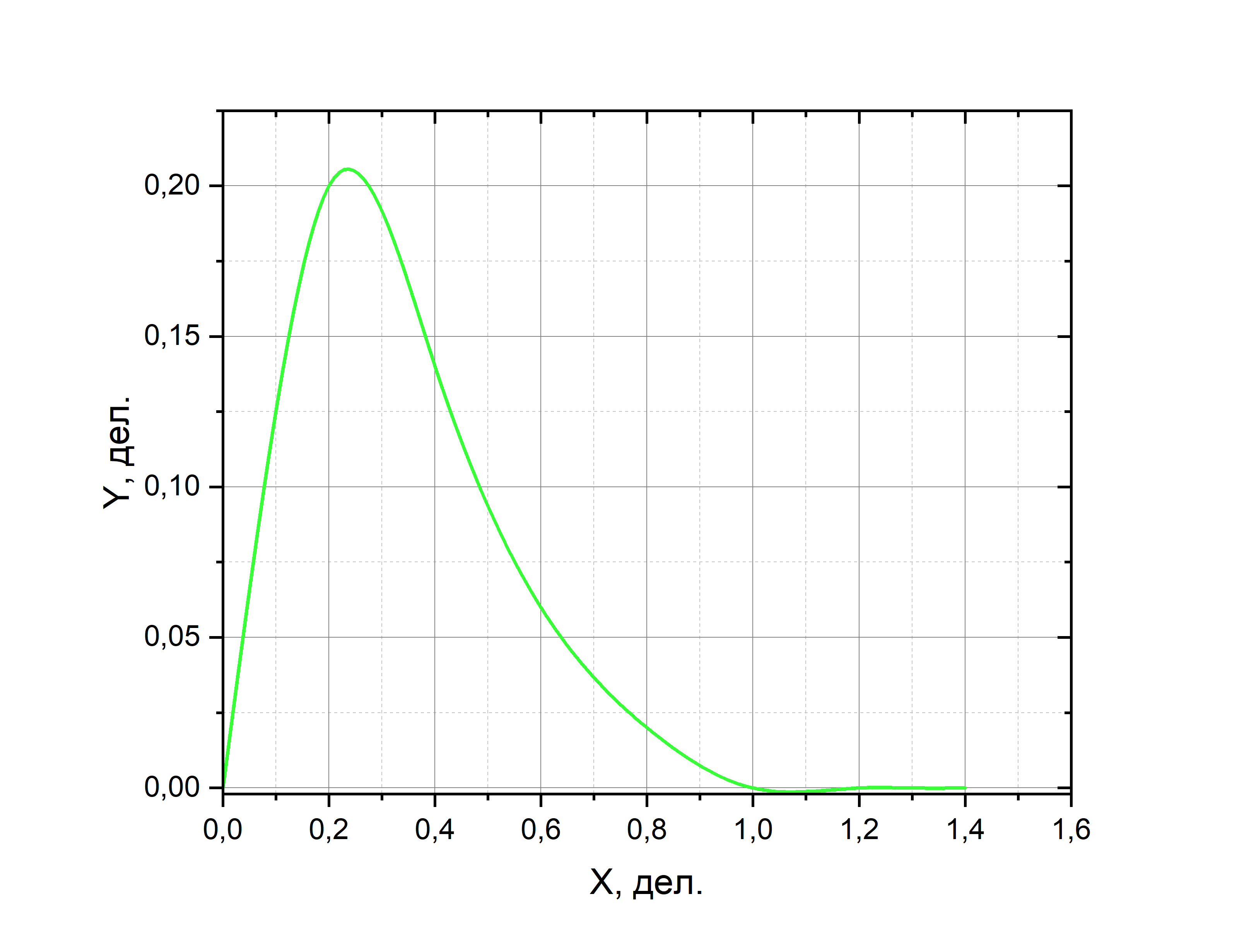

Рассчитаем собственные частоты цепи:
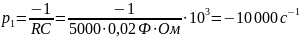
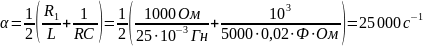
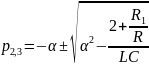
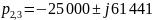
Рис.16. - Собственные частоты
свободного процесса в цепи третьего
порядка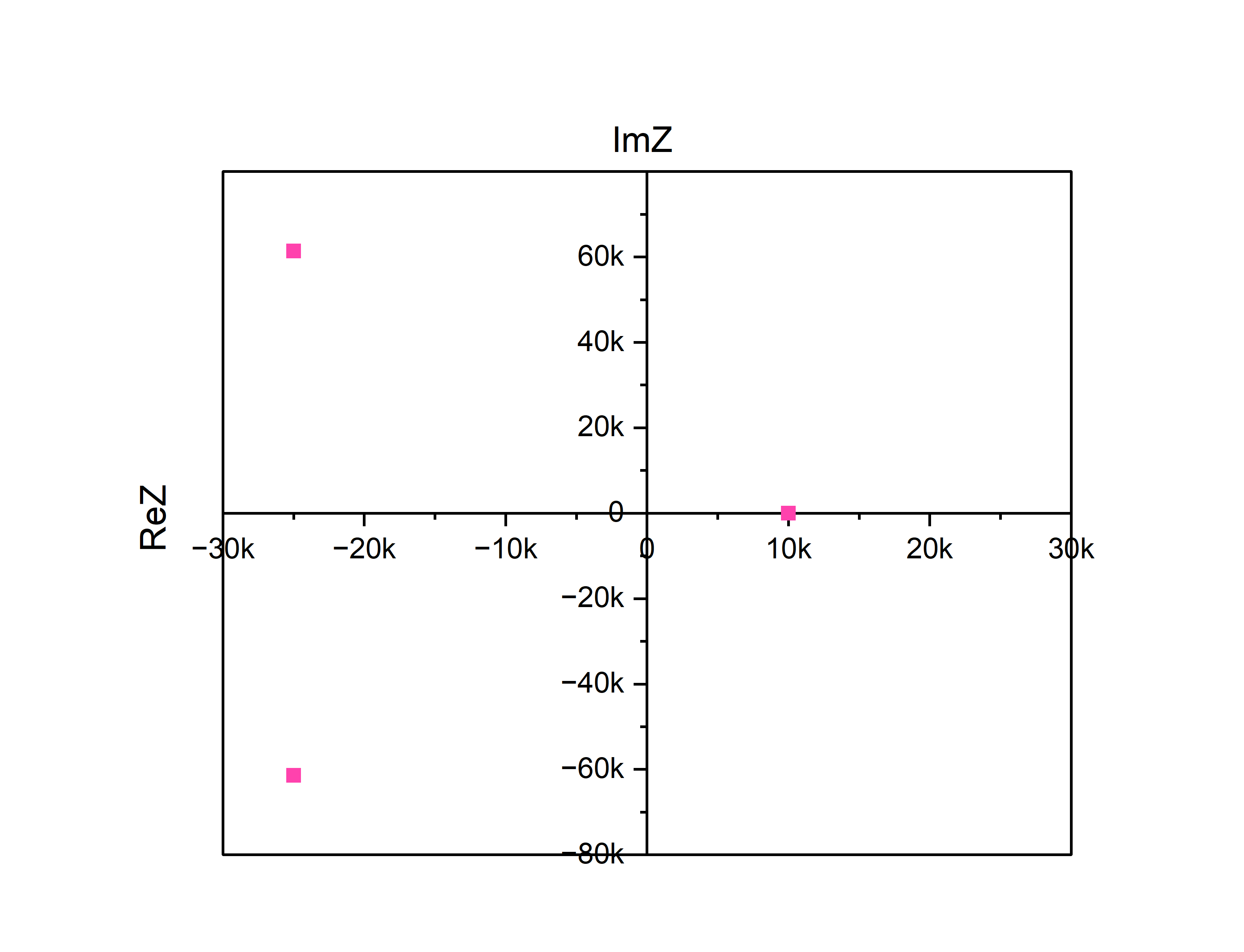

Вывод
Сравним определенные экспериментально и теоретически собственные частоты в таблице 1.
Таблица 1 – Экспериментальные и теоретические значения собственных частот.
Теоретические значения |
Экспериментальные значения |
Свободные процессы в цепи первого порядка |
|
|
|
Колебательный режим |
|
|
|
Апериодический режим |
|
|
- |
Критический режим |
|
|
|
Свободные процессы в цепи третьего порядка |
|
|
- |
Теоретические и экспериментальные собственные частоты для цепи первого порядка близки по значению. Небольшое расхождение может быть связано с неточностью измерений, отличием реального значения номиналов электронных компонентов от использованных при расчете. Те же выводы справедливы для собственных частот колебательного режима.
Теоретические
значения собственных частот, рассчитанные
при
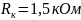 не соответствуют критическому режиму.
Это может быть связано с неточностью
потенциометра.
не соответствуют критическому режиму.
Это может быть связано с неточностью
потенциометра.
Рассчитанная
добротность контура в колебательном
режиме
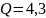 ,
что соответствует ожидаемому значению
,
что соответствует ожидаемому значению
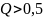 .
Добротность контура при
.
Добротность контура при
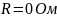 составила
составила
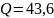 ,
что соответствует медленно затуханию
колебаний (можно наблюдать на рисунке
12).
,
что соответствует медленно затуханию
колебаний (можно наблюдать на рисунке
12).

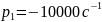
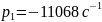
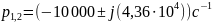
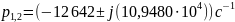
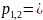 )
)