
диф зачет ИГ
.pdf@vcvvtw |
зачет ИГ |
32.Тело вращения. Образующая тела вращения.
Тело вращения
Тело вращения — это трёхмерная фигура, которая получается при вращении плоской фигуры (например, отрезка или кривой) вокруг оси.
Пример:
•Вращаем прямоугольник вокруг одной из его сторон → получаем цилиндр.
•Вращаем прямоугольный треугольник вокруг одного из катетов → получаем
конус.
•Вращаем полуокружность → получаем шар.
Образующая тела вращения
Образующая — это та самая линия, при вращении которой вокруг оси образуется поверхность тела.
•У цилиндра — образующей является прямая, перпендикулярная оси.
•У конуса — образующая тоже прямая, но наклонена к оси.
•У шара — образующая — дуга окружности (точнее, полуокружность).
>Образующая даёт форму телу — она "ведёт" его контур во время вращения.
@vcvvtw |
зачет ИГ |
33.Этапы построения аксонометрической проекции пирамиды.
чёткое и простое пошаговое руководство по построению аксонометрической проекции пирамиды, например, в прямоугольной изометрии:
1. Выбор типа проекции
На практике обычно используется прямоугольная изометрия, где все оси X, Y, Z под углом 120°, а коэффициенты искажения k = m = n = 1 (по ГОСТ 2.317–2011). То есть размеры откладываются без искажения.
2. Проведение аксонометрических осей
Из одной точки проводим три оси:
•X — вправо под углом 30°,
•Y — влево под углом 30°,
•Z — вертикально вверх (высота).
3.Построение основания пирамиды
Если пирамида прямоугольная с квадратным основанием, то:
1.Построй квадрат основания в плоскости XOY (горизонтальной): o откладывая стороны параллельно осям X и Y;
2.Отметь середину основания — это будет проекция основания точки вершины пирамиды.
4.Построение вершины
•Вдоль оси Z от центра основания отложи высоту пирамиды h — получаешь вершину пирамиды.
5.Соединение рёбер
•Соедини вершину пирамиды со всеми вершинами основания;
•В результате получишь рёбра боковых граней.
6.Оформление
•Очерти видимые рёбра сплошной основной линией;
•Невидимые — штриховыми, если нужно по условным обозначениям;
•При необходимости добавь размеры, оси симметрии, высоту.
@vcvvtw |
зачет ИГ |
34.Принцип определения точек боковой поверхности геометрических тел на
аксонометрических проекциях.
Что значит "точки боковой поверхности" в аксонометрии
Когда ты строишь геометрическое тело (например, призму, цилиндр, пирамиду) в
аксонометрической проекции, важно правильно определить точки, через которые пройдут рёбра или грани боковой поверхности. Это — опорные точки для прорисовки граней, рёбер и дуг в объёме.
Основной принцип
1.Выбирается основание тела (нижнее или верхнее), и его вершины строятся в аксонометрии:
o Например, у призмы — это многоугольник, o У цилиндра — эллипс,
o У пирамиды — многоугольник плюс вершина.
2.Находятся точки на соответствующей противоположной плоскости:
oТо есть на «верхней крышке» тела (если тело стоит на основании),
oИли на вершине (если пирамида),
oОтметив высоту вдоль оси Z (если основание лежит в плоскости XOY, как в изометрии).
3.Точки боковой поверхности определяются соединением одноимённых вершин основания и "крыши":
oУ призмы: соединяешь нижние и верхние вершины,
o У цилиндра: строишь вертикальные образующие (касательные к эллипсам), o У пирамиды: соединяешь основание с вершиной.
Как это выглядит в построении
Допустим, у нас прямоугольная призма:
•Строим нижнее основание — 4 точки, параллельные осям X и Y.
•От каждой вершины вверх по Z откладываем высоту — получаем 4 верхние точки.
•Соединяем нижнюю и верхнюю вершины: получаем рёбра боковой поверхности
@vcvvtw |
зачет ИГ |
35.Этапы определения проекций точек боковой поверхности конуса
методом вспомогательной образующей.
Исходные данные:
Пусть задан конус с:
•основанием в горизонтальной плоскости (OX–OY),
•вершиной на оси Z,
•заданным радиусом основания и высотой.
Этапы построения методом вспомогательной образующей:
1. Построение основания и оси конуса в аксонометрии
o Основание (круг) проецируется как эллипс в аксонометрии (обычно в изометрии), o Вершину конуса (точку S) откладывают вверх по оси Z от центра основания.
2. Построение вспомогательных образующих
o Отмечают равномерные точки на эллипсе основания (например, каждые 30° или 45°),
oИз этих точек проводят вспомогательные прямые, соединяющие вершину конуса с каждой точкой на основании — это и есть вспомогательные образующие.
3. Определение точки на поверхности
o Задаём точку M, лежащую на какой-то из образующих, например: – либо по заданной высоте от основания, – либо через пересечение сечущей плоскости.
4. Находим проекции точки M:
oОтмечаем положение точки M на конкретной вспомогательной образующей (то есть на отрезке от основания до вершины),
o Затем проецируем эту точку на плоскости (например, на горизонтальную и фронтальную),
oПолучаем проекции M (горизонтальная), M (фронтальная) и при необходимости M (профильная).
5.Повторяем для других точек сечения или грани Таким образом, можно получить несколько точек, через которые проходит сечение или контур, и соединить их гладкой кривой или ломаной.
Почему этот метод удобен:
Метод помогает найти точки на сложной поверхности, проанализировать её и точно построить
сечение, разрез, проекцию элемента. Особенно полезен при изображении наклонных сечений.
@vcvvtw |
зачет ИГ |
36.Этапы определения проекций точек боковой поверхности конуса
методом вспомогательной окружности.
Метод вспомогательной окружности
Этот метод используется для определения проекций точек на боковой поверхности конуса, особенно при построении сечений, разрезов и развёрток.
Этапы построения проекций точек методом вспомогательной окружности:
1. Построй основание конуса и его ось
oОснование — это окружность, проецируемая (на π ) как окружность или
эллипс,
oОсь — отрезок от центра основания до вершины (обычно вертикальна в фронтальной проекции).
2.Раздели основание на несколько равных частей — например, на 8 или 12 точек.
Эти деления обозначают точки касания образующих.
3.Проведи через вершину конуса прямые к этим точкам основания — это и будут образующие боковой поверхности.
4.Выбери одну или несколько вспомогательных горизонтальных плоскостей — они будут пересекать конус, образуя вспомогательные окружности (сечения параллельные основанию).
5.Построй вспомогательную окружность в сечении — радиус берётся пропорционально высоте сечения, — центр этой окружности на оси конуса.
6.На вспомогательной окружности отметь те же деления, что и на основании —
например, если основание поделено на 8 точек, делим и вспомогательную окружность на 8.
7.Проецируй эти точки на нужные плоскости проекций — точки вспомогательной окружности, полученные пересечением с образующими, будут лежать на боковой поверхности конуса.
Для чего этот метод нужен:
•Он позволяет точно определить точки на боковой поверхности без сложных вычислений.
•Применяется при построении сечений, разрезов, развёрток конуса.
@vcvvtw |
зачет ИГ |
37.Получение действительной величины фигуры сечения способом замены
плоскостей проекций для усеченной многогранника (призма).
Суть задачи:
Фигура сечения, полученная при пересечении многогранника (призмы) наклонной плоскостью, имеет искажённую форму в основных проекциях. Чтобы увидеть её в истинной (действительной) величине, применяют метод замены плоскостей проекций.
Этапы построения:
1.Построить комплексный чертёж призмы и секущей плоскости
•Построить фронтальную и горизонтальную проекции призмы.
•Провести секущую плоскость (например, наклонную к основанию), задать её через 3 точки или по следам.
2.Определить проекции точек пересечения секущей плоскости с рёбрами призмы
•Находятся точки, где плоскость пересекает боковые рёбра многогранника.
•Эти точки формируют фигуру сечения (обычно — многоугольник).
3.Выбрать новую плоскость проекций, параллельную плоскости сечения
•Это ключевой шаг! Новая плоскость проекций «смотрит» прямо на фигуру сечения
— сечение будет отображаться в истинную величину.
4.Построить новую проекцию — с заменой плоскостей
•Через каждую точку сечения провести линии связи (перпендикуляры к новой плоскости).
•Определить расстояния этих точек до оси замены (обычно берутся из фронтальной проекции) и отложить их на новой плоскости.
5.Соединить полученные точки на новой проекции
•Полученный многоугольник и будет фигурой сечения в её действительной величине.
Примечание:
•Метод особенно удобен, когда плоскость сечения не перпендикулярна ни одной из основных плоскостей.
•Чертёж часто оформляют с дополнительной координатной сеткой и осью замены
(ось z′).
@vcvvtw |
зачет ИГ |
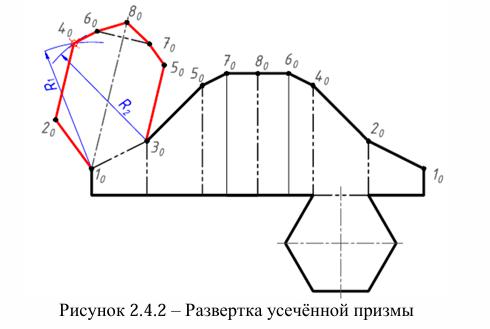
38.Этапы построения развертки полной поверхности усеченной призмы.
•Проведение базовой линии
•Проводим горизонтальную прямую.
•На ней откладываем отрезки, равные длинам сторон основания призмы (в порядке обхода основания).
•Построение перпендикуляров
•Из каждой вершины основания восстанавливаем перпендикуляры вверх.
•Отложение высот рёбер
•По перпендикулярам от основания вверх откладываются высоты боковых рёбер (берутся из фронтальной или профильной проекции).
•Построение точек верхнего основания
•Полученные точки (точки пересечения высот) и есть вершины усечённого основания: 10, 20, ...,
80.
•Соединение точек
•Вершины соединяются ломаной кривой, описывая верхнюю грань развёртки.
•Построение нижнего основания
•К нижней части развёртки добавляется многоугольник основания (форма и размер исходной призмы).
•Построение фигуры сечения
•К верхней части развёртки достраивается фигура, которая повторяет форму секущего сечения.
•Метод триангуляции
•Для нахождения точек (например, точки 40):
o Из точки 10 чертим дугу радиусом R = |10–40| (из истинной величины), o Из точки 30 — дугу радиусом R = |30–40|,
o Пересечение дуг — точка 40.
•Аналогично определяются остальные точки верхнего основания.
@vcvvtw |
зачет ИГ |
39.Получение действительной величины фигуры сечения способом
совмещения плоскостей проекций для усеченного тела вращения
(цилиндр).
Найти действительную величину сечения, полученного в результате пересечения усечённого цилиндра наклонной плоскостью. Используется метод совмещения плоскостей проекций (его ещё называют методом вращения или методом параллельного переноса).
Этапы построения:
1.Построение комплексного чертежа цилиндра
•Начерти основание цилиндра (в проекции — окружность или прямоугольник),
•Обозначь ось симметрии,
•Построй второе основание (цилиндр будет прямой),
•Проведи секущую плоскость — наклонную (не параллельную основанию).
2.Определение точек пересечения
•Выдели места, где секущая плоскость пересекает боковую поверхность цилиндра (обычно это проекции точек на образующих).
3.Выбор плоскости совмещения
•Выбирается новая плоскость проекций, параллельная секущей плоскости, чтобы фигура сечения на ней отображалась в истинную величину.
4.Совмещение плоскостей
•Через точку пересечения образующей и секущей проводят оси совмещения (например, перпендикуляр к проекции секущей),
•Каждую точку сечения переносят на новую плоскость:
o по линиям связи,
oс сохранением расстояния от базовой линии (основывается на фронтальной/профильной проекции).
5.Построение фигуры сечения
•Соединяются проецированные точки в новом положении,
•Полученная фигура — и есть истинная форма сечения.
Пример:
Если секущая плоскость режет цилиндр наклонно, в виде эллипса, то в проекциях она может выглядеть как трапеция, и только в совмещённой плоскости (на новой координатной сетке) получится точная эллиптическая форма.
@vcvvtw |
зачет ИГ |
40.Назначение изображений на чертеже. Расположение предметов при
прямоугольном проецировании.
Назначение изображений на чертеже
Изображения на чертеже (виды, разрезы, сечения) служат для наглядного и
однозначного представления формы, размеров и конструктивных особенностей изделия. Их цель — передать информацию так, чтобы:
•можно было изготовить и контролировать изделие,
•не требовалось дополнительных пояснений или 3D-моделей,
•чертёж был универсально понятен другим специалистам (технологам, инженерам, монтажникам и т. д.).
>Главное правило: все изображения на чертеже выполняются по методу прямоугольного (ортогонального) проецирования, принятым в ЕСКД (ГОСТ 2.305–
2008).
Расположение предметов при прямоугольном проецировании
В основе — куб или шесть плоскостей проекций. Предмет мысленно помещают внутрь него, и получаются 6 основных видов:
Вид |
На какой плоскости |
Расположение на чертеже |
Вид спереди Фронтальная π |
Главный вид, в центре |
|
Вид сверху |
Горизонтальная π |
Под видом спереди |
Вид слева |
Профильная π |
Справа от вида спереди |
Вид справа |
Профильная π ′ |
Слева от вида спереди |
Вид снизу |
Горизонтальная π ′ |
Над видом спереди |
Вид сзади |
Фронтальная π ′ |
Справа от вида слева (или отдельно) |
|
|
|
По ГОСТу, если виды расположены в проекционной связи, их не подписывают. В
остальных случаях используют обозначение — например: A, A–A.
Выбор главного вида важен: он должен давать наиболее полное представление о назначении и устройстве изделия. По нему выстраиваются и другие виды, сечения и разрезы.
@vcvvtw |
зачет ИГ |
41.Основные плоскости проекций. Что принимают в качестве главного
изображения. Количество изображений на чертеже.
Основные плоскости проекций
В начертательной геометрии и инженерной графике используются три взаимно перпендикулярные плоскости проекций:
1.Горизонтальная плоскость (π ) — вид сверху (план),
2.Фронтальная плоскость (π ) — вид спереди (главный вид),
3.Профильная плоскость (π ) — вид слева (или справа).
>Пересечение этих плоскостей образует трёхгранный угол, в который мысленно помещают объект для построения его проекций.
Главное изображение на чертеже
Вкачестве главного изображения (или главного вида) принимается проекция, которая:
•наилучшим образом раскрывает форму, конструкцию и назначение изделия,
•отображает объект в его характерном положении при эксплуатации или изготовлении,
•используется как отправная точка для расположения остальных видов, сечений и разрезов.
По ГОСТу главный вид располагается в центре листа и проецируется на фронтальную плоскость.
Количество изображений на чертеже
Количество видов, разрезов и сечений зависит от сложности детали:
•Минимум — один вид, если он полностью раскрывает форму объекта.
•Чаще всего — два или три вида (вид спереди, сверху и слева).
•При сложной геометрии добавляют дополнительные виды, разрезы, сечения или выносные элементы.
>ГОСТ рекомендует: число изображений должно быть минимальным, но достаточным для понимания и изготовления изделия — без потери точности или нужды в дополнительных пояснениях.
