Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ ФУНКЦИИ В ТАБЛИЧНОМ И АНАЛИТИЧЕСКОМ ВИДЕ

Отчет по лабораторной работе №3

по дисциплине «Численные методы»

Студент гр. 733-1

_______Сметанников Д.Е

Принял:

ст.преп. каф. КИБЭВС

_______Катаева Е.С

Содержание

1 Введение 3

2 Ход работы 5

7

Заключение 19

Приложение А 20

1. Введение

Цель работы – построение квадратного интерполяционного полинома Лагранжа для последовательности точек и для функции в аналитическом виде. Построение аппроксимирующей квадратной функции для последовательности точек и для функции в аналитическом виде. Прогнозирование значения функции с помощью интерполирующей и аппроксимирующей функции. Вычисление промежуточной точки с помощью интерполирующей и аппроксимирующей функции.

Вариант задания представлены на рис. 1-3

Р исунок 1 — Задание 1

Р исунок 2 — Задание 2

Р исунок 3 — Задание 3

2. Ход работы

Составим таблицы значений для построений и сравнений графиков из заданий 2 и 3.

Результат работы представлены в таблицах 1 и 2.

Таблица 1 — Задание 2

x	y
0.0	0.000000
0.2	1.094532
0.4	1.547902
0.6	1.895785
0.8	2.189064
1.0	2.447448
1.2	2.681045
1.4	2.895859
1.6	3.095804
1.8	3.283596
2.0	3.461214
2.2	3.630152
2.4	3.791570
2.6	3.946391
2.8	4.095363

Таблица 2 — Задание 3

x	y
0.0	1.000000
0.2	0.464258
0.4	-0.568930
0.6	-0.992518
0.8	-0.352638
1.0	0.665088
1.2	0.970182
1.4	0.235742
1.6	-0.751293
1.8	-0.933328
2.0	-0.115317
2.2	0.826255
2.4	0.882507
2.6	-0.006833
2.8	-0.888852

Построим графики из таблицы значений задания 1 и для уравнений из заданий 2 и 3.

Результаты представлены на рисунках 1-3.

Р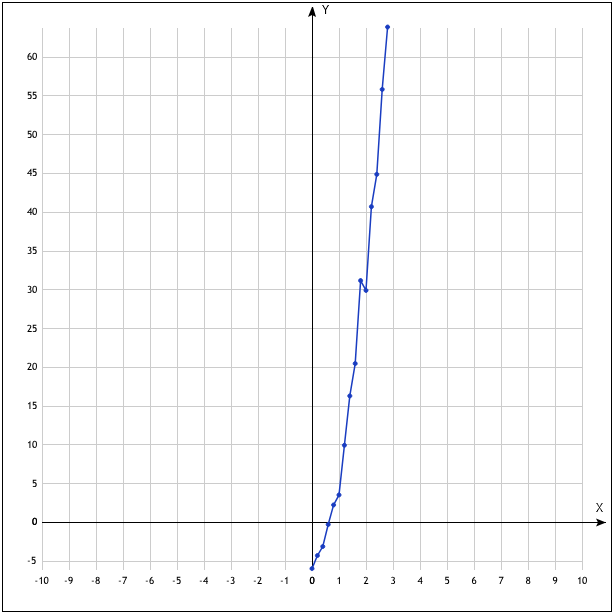 исунок 1 — График для задания 1

Р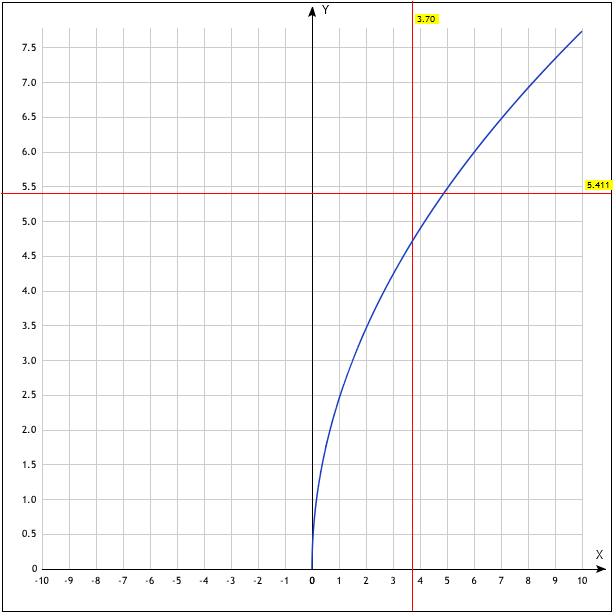 исунок 2 — График для уравнения из задания 2.

Р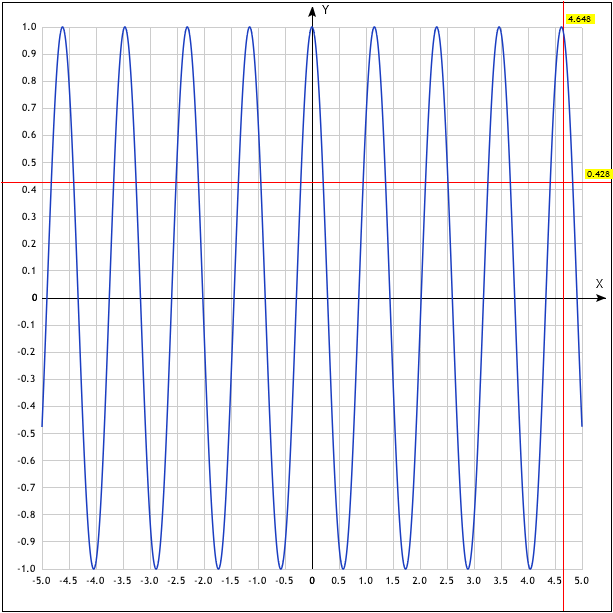 исунок 3 — График для уравнения из задания 3

Формула вычисляемого полинома представлена в виде

Процесс выбора узлов для точки x:

Для вычисления полинома Лагранжа выбираются три последовательные узла из заданного набора. Если вводится значение x, программа находит последние узлы, которые соответствуют x и берёт следующие два узла для построения полинома второго порядка.

Результат работы программы представлен на рисунке 4.

Р исунок 4 — Результат работы программы

Код программы можно наблюдать в приложении А

При округлении до 4 знаков после запятой полученных значений {x1 = 0.0; y1 = -5.9478}, {x2 = 0.0; y2 = 0}, {x3 = 0.0; y3 = 1} мы сравним их с табличными и можем увидеть, что они совпадают, что доказывает эффективность метода интерполяции полинома Лагранжа.

Для построения аппроксимирующей функции с помощью метода наименьших квадратов используется система уравнений, которая формируется следующим образом:

Суммы:

;

;

;

;

.

Система уравнений:

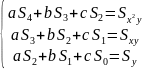
Результат работы программы представлен на рисунке 5.

Р исунок 5 — Результат работы программы

Уравнения полученных функций:

6,9396x^2 + 5,6083x + -6,2707

-0,3885x^2 + 2,3349x + 0,4531

0,0844x^2 + -0,3384x + 0,2744

Совместные графики функции и узлов представлены на рисунках 6.1-6.3.

Р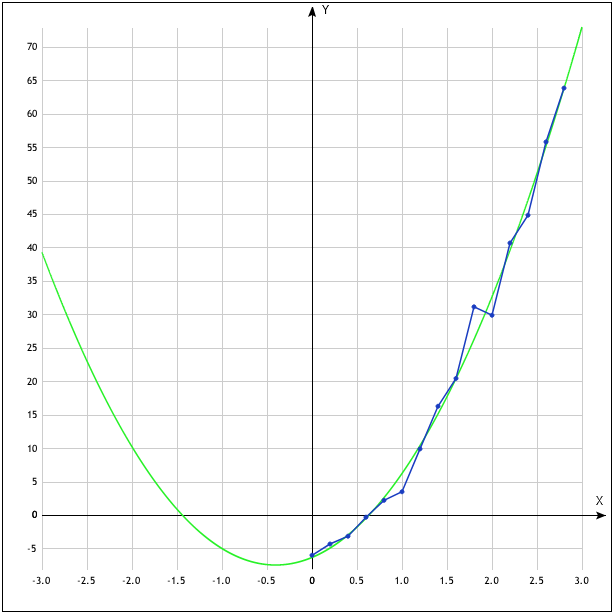 исунок 6.1 – График y1

Р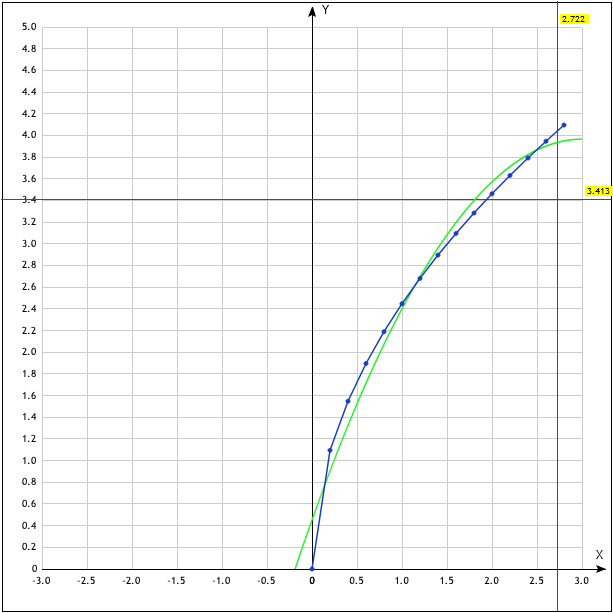 исунок 6.2 – График y2

Р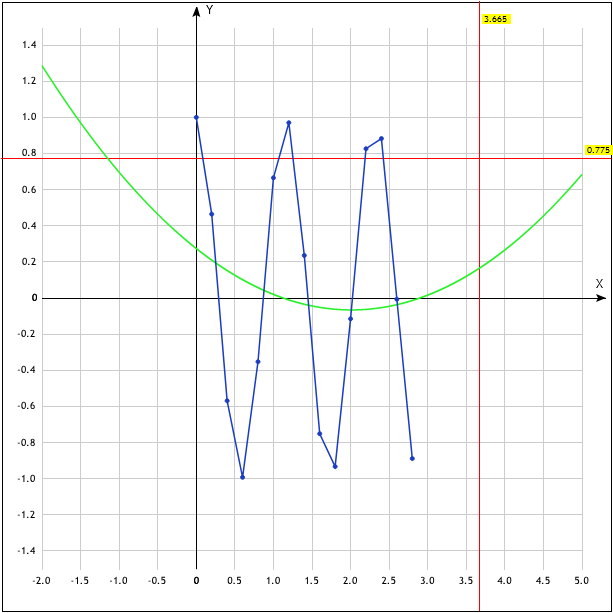 исунок 6.3 – График y3

По итогам работы для каждой заданной последовательности точек составим сводные таблицы результатов (таблицы 3-3.2).

Таблица 3 – функция y1

Узел	Промежуточная точка x*	Прогнозная точка ​	Прогнозная точка ​	Значение	Значение	Прогноз	Прогноз
1.0	0.9	3.0	4.5	3,5507	3,0609	73,0102	159,4926

Таблица 3.1 – функция y2

Узел	Промежуточная точка x*	Прогнозная точка ​	Прогнозная точка ​	Значение	Значение	Прогноз	Прогноз
1.0	0.9	3.0	4.5	2,4474	2,3226	3,9613	3,0931

Таблица 3.2 – функция y3

Узел	Промежуточная точка x*	Прогнозная точка ​	Прогнозная точка ​	Значение	Значение	Прогноз	Прогноз
1.0	0.9	3.0	4.5	0,6651	0,109	0,0184	0,4598

Ниже представлены сводные таблицы (таблицы 3.3-3.5) результатов, в которой указаны вычисленные значения и соответствующие погрешности для каждой функции.

Таблица 3.3 – Сводная таблица y1

x	y(x)	L2(x)	∆𝑥 = |𝑦(𝑥) − 𝐿2(𝑥)|		∆𝑥 = |𝑦(𝑥) − |
	3,5507	3,5507	0	6,2771	2.73
x* = 0.9	-	3,0609	-	4,3978	-
​	-	69,0042	-	73,0102	-
​	-	14,3178	-	159,4926	-

Таблица 3.4 – Сводная таблица y2

x	y(x)	L2(x)	∆𝑥 = |𝑦(𝑥) − 𝐿2(𝑥)|		∆𝑥 = |𝑦(𝑥) − |
	2.45	2.45	0	2.4	0.05
x* = 0.9	2.32	2.32	0	2.24	0.08
​	4.24	4.24	0	3.96	0.28
​	5.13	5.13	0	3.09	2.04

Таблица 3.5 – Сводная таблица y3

x	y(x)	L2(x)	∆𝑥 = |𝑦(𝑥) − 𝐿2(𝑥)|		∆𝑥 = |𝑦(𝑥) − |
	0.67	0.67	0	0.02	0.64
x* = 0.9	-0.17	0.11	0.28	0.04	0.21
​	-0.79	-1.76	0.98	0.02	0.81
​	0.36	-8.09	8.45	0.46	0.1

Цель интерполяции — обеспечить точное совпадение с исходными значениями функции в заданных точках, что полезно для табличных данных или дискретных измерений, требующих высокой точности.

Аппроксимация, напротив, сглаживает данные и лучше подходит для анализа общего поведения функции, особенно при наличии погрешностей.

Выбор метода зависит от вида функции: для функций с резкими изменениями интерполяция даёт точные значения в узлах, но на прогнозных точках может иметь большие отклонения. Для гладких функций аппроксимация лучше отражает общую тенденцию и обеспечивает меньшие погрешности.