
ЛР3 / ЧМ_Л3
.pdfМинистерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронновычислительных систем (КИБЭВС)
ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ ФУНКЦИИ В ТАБЛИЧНОМ И АНАЛИТИЧЕСКОМ ВИДЕ
Отчет по лабораторной работе №3 по дисциплине «Численные методы»
Студент гр. 733-1
_______Сметанников Д.Е
Принял:
ст.преп. каф. КИБЭВС
_______Катаева Е.С
Томск 2024
|
|
Содержание |
1 |
Введение ................................................................................................................. |
3 |
2 |
Ход работы ............................................................................................................. |
5 |
|
................................................................................................................................. |
6 |
........................................................................................................... |
Заключение |
19 |
...................................................................................................... |
Приложение А |
20 |
2

1Введение
Цель работы – построение квадратного интерполяционного полинома Лагранжа для последовательности точек и для функции в аналитическом виде. Построение аппроксимирующей квадратной функции для последовательности точек и для функции в аналитическом виде. Прогнозирование значения функции с помощью интерполирующей и аппроксимирующей функции. Вычисление промежуточной точки с помощью интерполирующей и аппроксимирующей функции.
Вариант задания представлены на рис. 1-3
Рисунок 1 — Задание 1
Рисунок 2 — Задание 2
3

Рисунок 3 — Задание 3
4
2Ход работы
Составим таблицы значений для построений и сравнений графиков из
заданий 2 и 3.
Результат работы представлены в таблицах 1 и 2.
|
Таблица 1 — Задание 2 |
x |
y |
0.0 |
0.000000 |
0.2 |
1.094532 |
0.4 |
1.547902 |
0.6 |
1.895785 |
0.8 |
2.189064 |
1.0 |
2.447448 |
1.2 |
2.681045 |
1.4 |
2.895859 |
1.6 |
3.095804 |
1.8 |
3.283596 |
2.0 |
3.461214 |
2.2 |
3.630152 |
2.4 |
3.791570 |
2.6 |
3.946391 |
2.8 |
4.095363 |
5
|
Таблица 2 — Задание 3 |
x |
y |
0.0 |
1.000000 |
0.2 |
0.464258 |
0.4 |
-0.568930 |
0.6 |
-0.992518 |
0.8 |
-0.352638 |
1.0 |
0.665088 |
1.2 |
0.970182 |
1.4 |
0.235742 |
1.6 |
-0.751293 |
1.8 |
-0.933328 |
2.0 |
-0.115317 |
2.2 |
0.826255 |
2.4 |
0.882507 |
2.6 |
-0.006833 |
2.8 |
-0.888852 |
Построим графики из таблицы значений задания 1 и для уравнений
из заданий 2 и 3.
Результаты представлены на рисунках 1-3.
6

Рисунок 1 — График для задания 1
7

Рисунок 2 — График для уравнения из задания 2.
8
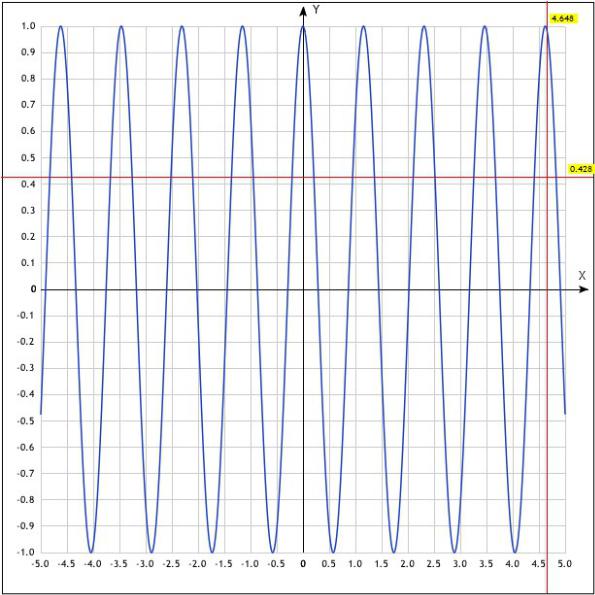
Рисунок 3 — График для уравнения из задания 3
Формула вычисляемого полинома представлена в виде
L2 |
(x )= |
(x−x1)(x−x2) |
y0 |
+ |
(x−x0 )(x−x2) |
y1 |
+ |
(x−x0 )(x−x1) |
y2 |
|||||
(x0 |
−x1)(x0−x |
2) |
(x1−x0 )(x1−x |
2) |
(x2−x0 )(x2 – x |
1) |
||||||||
|
|
|
|
|
|
|
||||||||
9

Процесс выбора узлов для точки x:
Для вычисления полинома Лагранжа выбираются три последовательные узла из заданного набора. Если вводится значение x, программа находит последние узлы, которые соответствуют x и берёт следующие два узла для построения полинома второго порядка.
Результат работы программы представлен на рисунке 4.
Рисунок 4 — Результат работы программы
Код программы можно наблюдать в приложении А
При округлении до 4 знаков после запятой полученных значений {x1 = 0.0; y1 = -5.9478}, {x2 = 0.0; y2 = 0}, {x3 = 0.0; y3 = 1} мы сравним их с табличными и можем увидеть, что они совпадают, что доказывает эффективность метода интерполяции полинома Лагранжа.
Для построения аппроксимирующей функции с помощью метода наименьших квадратов используется система уравнений, которая формируется следующим образом:
10
