ЛР2 / ЧМ_Л2
.odtМинистерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Отчет по лабораторной работе №2
по дисциплине «Численные методы»
Студент гр. 733-1
_______Сметанников Д.Е
Принял:
ст.преп. каф. КИБЭВС
_______Катаева Е.С
Содержание
1 Введение 3
2 Ход работы 4
Заключение 6
Приложение А 7
Введение
Цель работы – освоить методы отделения и уточнения решения систем нелинейных уравнений
Вариант задания представлен на рис. 1
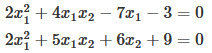
Рисунок 1 — Задание
Ход работы
Для начала необходимо построить график для следующей системы:
График
представлен на рисунке 1.
Рисунок
1 — График системы уравнений
В результате построения графика можно заметить, что существую всего два корня, находящиеся в диапазонах:
−4.2 ≤ 𝑥 ≤ −0.4
−0.2 ≤ y ≤ 0.6
Само решение будет проводиться методом Ньютона через матрицы, реализованным кодом. Результат выполнения программы можно наблюдать на рисунке 2.
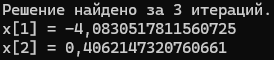
Рисунок 2 — Результат работы
Код программы можно наблюдать в приложении А
|
Начальная точка |
Число итераций |
Решение |
Проверочная система |
x0=(1,1)T |
6 |
X=(1.545, 1.502)T |
Индивидуальная система |
x0 = (-4.1, -0.5)T |
3 |
X=(-4.08,0.4)T |
Заключение
В результате выполнения данной лабораторной работы были освоены отделения и уточнения решения систем нелинейных уравнений.
Приложение А
(обязательное)
Код для задания 1
class Program
{
static double[,] Jacobian(Func<double[], double>[] f, double[] x, double h)
{
int n = x.Length;
double[,] J = new double[n, n];
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
double[] x_forward = (double[])x.Clone();
x_forward[j] += h;
double[] x_backward = (double[])x.Clone();
x_backward[j] -= h;
J[i, j] = (f[i](x_forward) - f[i](x_backward)) / (2 * h);
}
}
return J;
}
static double[] GaussSolve(double[,] A, double[] b)
{
int n = A.GetLength(0);
double[] x = new double[n];
for (int i = 0; i < n; i++)
{
int maxRow = i;
for (int k = i + 1; k < n; k++)
{
if (Math.Abs(A[k, i]) > Math.Abs(A[maxRow, i]))
maxRow = k;
}
for (int j = 0; j < n; j++)
{
double temp = A[i, j];
A[i, j] = A[maxRow, j];
A[maxRow, j] = temp;
}
double tempB = b[i];
b[i] = b[maxRow];
b[maxRow] = tempB;
for (int k = i + 1; k < n; k++)
{
double factor = A[k, i] / A[i, i];
for (int j = i; j < n; j++)
{
A[k, j] -= factor * A[i, j];
}
b[k] -= factor * b[i];
}
}
for (int i = n - 1; i >= 0; i--)
{
x[i] = b[i] / A[i, i];
for (int k = i - 1; k >= 0; k--)
{
b[k] -= A[k, i] * x[i];
}
}
return x;
}
static (double[], int) NewtonMethod(Func<double[], double>[] f, double[] x0, double tol, int maxIter)
{
int n = x0.Length;
double[] x = (double[])x0.Clone();
double h = 1e-5;
for (int iter = 0; iter < maxIter; iter++)
{
double[] F = new double[n];
for (int i = 0; i < n; i++)
{
F[i] = -f[i](x);
}
double[,] J = Jacobian(f, x, h);
double[] deltaX = GaussSolve(J, F);
bool stop = true;
for (int i = 0; i < n; i++)
{
if (Math.Abs(deltaX[i]) >= tol || Math.Abs(F[i]) >= tol)
{
stop = false;
break;
}
}
if (stop)
return (x, iter + 1);
for (int i = 0; i < n; i++)
{
x[i] += deltaX[i];
}
}
throw new Exception("Метод Ньютона не сошелся за указанное число итераций");
}
static double F1(double[] x)
{
return 2 * Math.Pow(x[0], 2) - 12 * x[0] * x[1] + 15 * x[0] + 8;
}
static double F2(double[] x)
{
return 2 * Math.Pow(x[0], 2) + 9 * x[0] * x[1] + 5 * x[0] + 2;
}
static void Main()
{
Func<double[], double>[] f = { F1, F2 };
double[] x0 = { -4.1, -0.5 };
double tol = 0.001;
int maxIter = 100;
try
{
var (solution, iterations) = NewtonMethod(f, x0, tol, maxIter);
Console.WriteLine($"Решение найдено за {iterations} итераций.");
for (int i = 0; i < solution.Length; i++)
{
Console.WriteLine($"x[{i + 1}] = {solution[i]}");
}
}
catch (Exception e)
{
Console.WriteLine(e.Message);
}
}
}
Томск 2024