
ЛР1 / ЧМ_Л1 финал
.pdfМинистерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронновычислительных систем (КИБЭВС)
ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ Отчет по лабораторной работе №1
по дисциплине «Численные методы»
Студент гр. 733-1
_______Сметанников Д.Е
Принял:
ст.преп. каф. КИБЭВС
_______Катаева Е.С
Томск 2024
|
|
Содержание |
1 |
Введение................................................................................................................ |
.3 |
2 |
Ход работы............................................................................................................. |
4 |
|
Заключение............................................................................................................. |
8 |
|
Приложение А........................................................................................................ |
9 |
|
Приложение Б..................................................................................................... |
.11 |

1Введение
Цель работы – освоить методы решения систем линейных алгебраических уравнений и решения нелинейных уравнений ( ) = 0 с одной переменной.
Варианты заданий представлены на рис. 1
Рисунок 1 — Задания
2Ход работы
Первым заданием является написание кода для программы, реализующей метод Зейделя, и его проверка на тестовой и индивидуальных системах.
Результаты выполнения кода для каждой из систем можно наблюдать на рисунках 2 и 3.
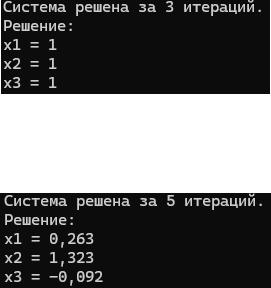
Рисунок 2 — Результат работы тестового задания
Рисунок 3 — Результат работы индивидуального задания
|
|
|
Таблица 1 |
|
|
|
|
|
Начальная точка |
Число итераций |
Решение |
|
|
|
|
Проверочная |
XO=(0,0,0)T |
3 |
X=(1, 1, 1)T |
система |
|
|
|
|
|
|
|
Индивидуальн |
XO=(0,0,0)T |
5 |
X=(0.263, 1.323, -0.092)T |
ая система |
|
|
|
|
|
|
|
Второе задание включает в себя реализацию кода, который должен решить нелинейное уравнение. Само решение происходит в 2 этапа, а именно этапы отделения и уточнения корня.
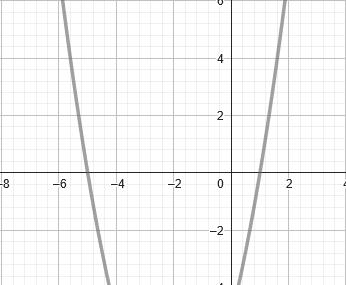
Первым делом построим график функции, который можно наблюдать на рисунке 4.
Рисунок 4 — График проверочной функции
На графике функции x^2+4x-5 можно наблюдать пересечение с осью абсцисс в промежутках [-6;-4] и [0;2], следовательно на данных отрезках имеются корни данной функции. В результате реализации кода были получены следующие корни: -5 и 1.
Результаты выполнения кода для можно наблюдать на рисунке 5.
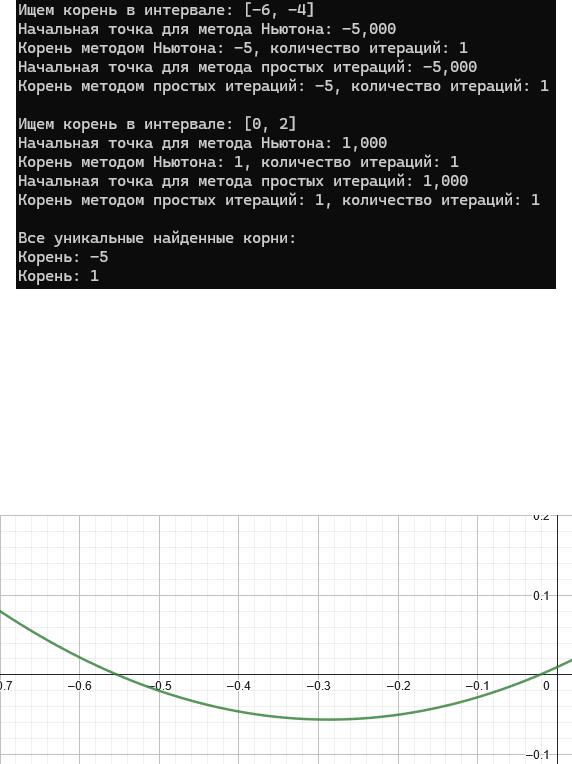
Рисунок 5 — Результат работы тестового задания
Далее, мы также строим график, но уже для индивидуальной функции 0.8x^2+0.46x+0.01. График функции можно наблюдать на рисунке 6.
Рисунок 6 — График индивидуальной функции Исходя из графика можно понять, что функция имеет 2 корня на
промежутках [-0.6, -0.5] и [-0.1, 0]. В результате реализации кода были получены следующие корни: -0.552 и -0.021.
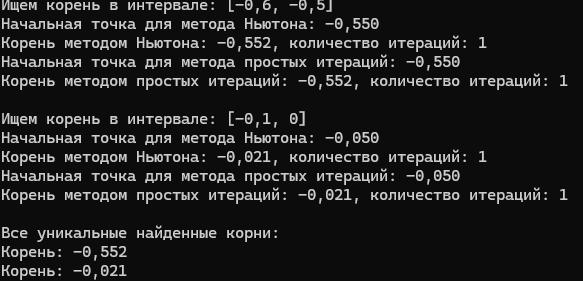
Результаты выполнения кода для можно наблюдать на рисунке 7.
Рисунок 7 — Результат работы индивидуального задания
Код программы можно наблюдать в приложении Б
|
|
|
|
Таблица 2 |
|
|
|
|
|
|
Начальная точка |
Число итераций |
Решение |
|
|
|
для каждого |
|
|
|
|
корня |
|
|
Метод |
XO=(-0,55, -0,05)T |
1,1 |
X=(-0,552, |
-0,021)T |
Ньютона |
|
|
|
|
Метод |
XO=(-0,55, -0,05)T |
1,1 |
X=(-0,552, |
-0,021)T |
простой |
|
|
|
|
итерации |
|
|
|
|
Заключение
В результате выполнения данной лабораторной работы были освоеныметоды решения алгебраических уравнений и решения нелинейных уравнений
( ) = 0 с одной переменной.
|
|
Приложение А |
|
|
(обязательное) |
|
|
Код для задания 1 |
double[,] k = |
|
|
{ |
|
|
{-10.28, 4.83, -5.27}, |
|
//{ 100, 2, 3}, |
{2.7, -4.33,0.02}, |
//{1, 100, 3}, |
|
{8.53,1.76,-12.94} |
|
//{1,2,100} |
}; |
|
|
double[] b = { 4.17, -5.02, 5.76 }; |
/*{ 105,104,103 };*/ |
|
double[] x0 = { 0, 0, 0 }; |
|
|
double[] prevX = new double[3]; |
|
|
double accuracy = 0.001; |
|
|
int iterations = 0; |
|
|
bool running = true; |
|
|
while (running)
{
prevX[0] = x0[0]; prevX[1] = x0[1]; prevX[2] = x0[2];
x0[0] = (b[0] - k[0, 1] * prevX[1] - k[0, 2] * prevX[2]) / k[0, 0]; x0[1] = (b[1] - k[1, 0] * x0[0] - k[1, 2] * prevX[2]) / k[1, 1]; x0[2] = (b[2] - k[2, 0] * x0[0] - k[2, 1] * x0[1]) / k[2, 2];
if (Math.Abs(x0[0] - prevX[0]) < accuracy &&
Math.Abs(x0[1] - prevX[1]) < accuracy && Math.Abs(x0[2] - prevX[2]) < accuracy)
{
Console.WriteLine($"Система решена за {iterations + 1} итераций."); running = false;
}
else
{
iterations++;
}
}
Console.WriteLine("Решение:"); for (int i = 0; i < 3; i++)
{
Console.WriteLine($"x{i + 1} = {Math.Round(x0[i], 3)} ");
}
