Министерство науки и высшего образования Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ

УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)

СТАТИСТИЧЕСКИЙ АНАЛИЗ ДАННЫХ

Отчет по индивидуальному заданию

по дисциплине «Теория вероятностей и математическая статистика»

Студент гр. 733-1

__________ Сметанников Д.Е

«___» __________ 2025 г.

Руководитель

Доцент каф. КИБЭВС, к.т.н.

_______ __________ Ю.В. Шабля

оценка

«___» __________ 2025 г.

Томск 2025

Оглавление

Введение 3

1 ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ 4

2 ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ 10

3 КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ 13

Заключение 20

Введение

Целью работы является закрепление полученных теоретических знаний в области математической статистики на примере выполнения практических задач с помощью специализированного программного обеспечения.

Задание:

1. Выбрать программное обеспечение для выполнения индивидуального задания;

2. Сформулировать исследуемый процесс, определить целевую функцию и влияющие факторы, сформировать выборку данных;

3. Выполнить проверку статистической гипотезы о виде закона распределения;

4. Провести однофакторный дисперсионный анализ;

5. Провести корреляционный и регрессионный анализ.

В качестве исследуемого процесса предлагается рассмотреть работу программы, реализующей сортировку пузырьком для массива убывающих чисел. Целевая функция (выходной параметр) – время сортировки массива. Фактор (входной параметр) – размер массива.

Для выполнения индивидуального задания выбрана программа для работы с электронными таблицами «Microsoft Excel».

1 Проверка статистических гипотез

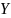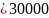Время сортировки массива принимает разные значения даже при одинаковых значениях входных параметров. Следовательно, можно принять время сортировки массива за некоторую случайную величину, которую обозначим как . Далее исследуем вид закона распределения случайной величины . Для этого с помощью исследуемой программы сформируем выборку при фиксированном значении входного параметра (размер массива элементов) с многократным повторением (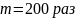 ). Фрагмент с результатами работы программы представлен на рисунке 1.1.

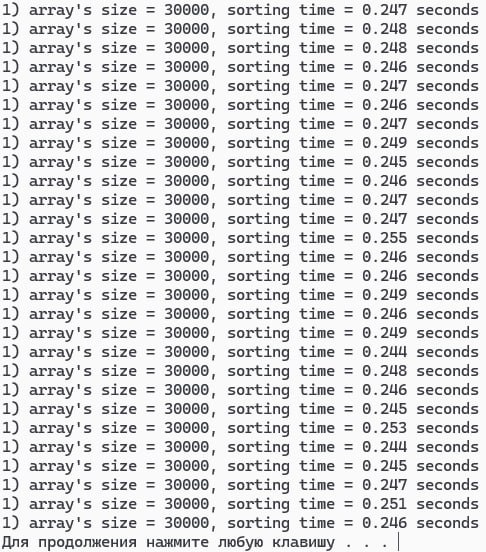
Рисунок 1.1 – Фрагмент с результатами работы программы

Все полученные значения были перенесены в «Microsoft Exсel». Так как случайная величина Y является непрерывной, то в полученной выборке присутствует большое значение различных значений случайной величины с малыми частотами их появления. Такую выборку невозможно исследовать на принадлежность к какому-либо виду закона распределения. Поэтому сгруппируем данные выборки, распределив их на равные интервалы значений, и посчитаем соответствующие частоты попадания в каждый интервал. Количество интервалов определяется по правилу Стёрджеса:

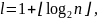
где 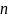– объем выборки. Тогда для исследуемой выборки получаем

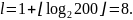
Полученное статистическое распределение выборки в виде интервального ряда представлено на рисунке 1.2.

Рисунок 1.2 – Статистическое распределение выборки

Далее на основе полученного статистического распределения выборки была построена гистограмма частот (рисунок 1.3).

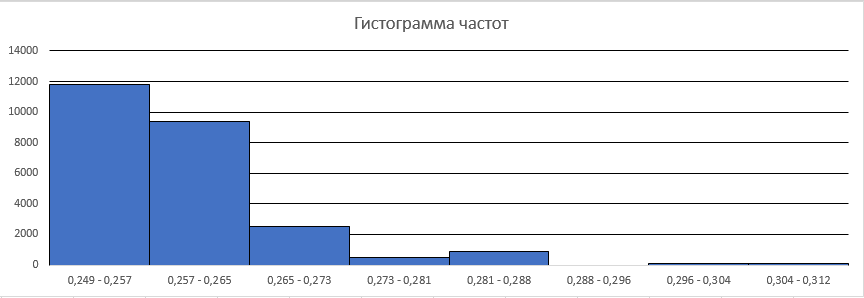
Рисунок 1.3 – Гистограмма частот

Исходя из графического представления полученной гистограммы частот, можно сделать следующие выводы о возможном законе распределения случайной величины : наиболее вероятный закон распределения – экспоненциальный, т.к. присутствуют характерные признаки, а именно:

• Резкий спад частот при увеличении значения;

• Мода и меридиан смещены к началу оси X;

Далее проверим статистическую гипотезу о виде закона распределения по критерию Пирсона. В качестве проверяемых законов распределения рассмотрим равномерное и нормальное распределения.

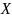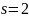Непрерывная случайная величина , распределенная по равномерному закону, определяется двумя параметрами ( ) и имеет следующие функцию плотности распределения вероятностей и функцию распределения вероятностей:

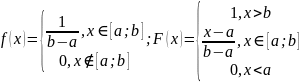
Для получения оценок параметров 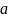и 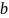равномерного распределения воспользуемся методом наибольшего правдоподобия:

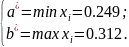
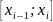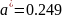Вычислим теоретические частоты попадания в интервал для равномерного распределения с параметрами и 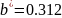при выборке объема 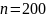по формуле:

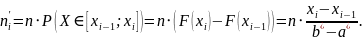
Вычислим расчетное значение критерия Пирсона по формуле

=

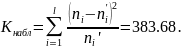
Определим критическое значение критерия Пирсона при уровне значимости 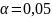по формуле

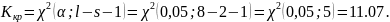
На рисунке 1.4 представлены подробности промежуточных вычислений.

Рисунок 1.4 – Расчеты для равномерного закона распределения

Так как 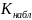> 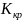, то H0, говорящее что распределение равномерное, отвергается.

Непрерывная случайная величина , распределенная по нормальному закону, определяется двумя параметрами ( ) и имеет следующие функцию плотности распределения вероятностей и функцию распределения вероятностей:

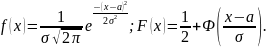
Для получения оценок параметров и 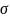нормального распределения воспользуемся методом наибольшего правдоподобия:

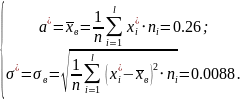
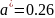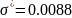Вычислим теоретические частоты попадания в интервал для нормального распределения с параметрами и при выборке объема по формуле:

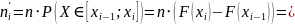
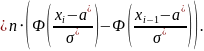
Вычислим расчетное значение критерия Пирсона по формуле

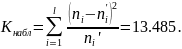
Определим критическое значение критерия Пирсона при уровне значимости по формуле

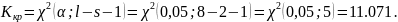
На рисунке 1.5 представлены подробности промежуточных вычислений.

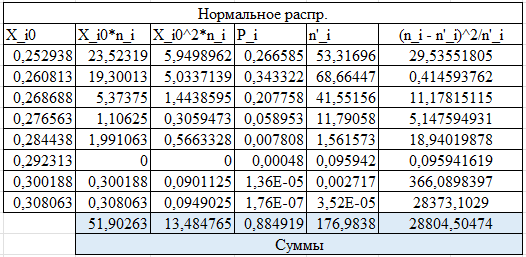
Рисунок 1.5 – Расчеты для нормального закона распределения

Так как > , то H0, говорящее что распределение нормальное, отвергается.