
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра безопасности информационных систем (БИС)
Графы Отчет по практической работе №6
по дисциплине «Структуры данных»
Студент гр. 733-1
_______ Сметанников Д.Е
_______
Принял:
преподаватель КИБЭВС
_______ Д.Р. Уразаев
_______
Томск 2024
Задание
Реализовать возможность работы с графом N узлов, M ребер. Выберете самостоятельно структуру. Обеспечьте следующие интерфейсные методы:
•ввод графа (можно случайным образом,можно вводить с клавиатуры) НЕДОПУСТИМО работать только с конечным числом ребер и узлов. Приложение должно позволять вводить разные графы.
•вывод графа - матрица смежности или весов
Вариант 7. Задана система дорог. Найти такой город, для которого сумма кратчайших расстояний до остальных городов максимальна.
2
|
|
Содержание |
|
Задание.................................................................................................................. |
.2 |
1 |
Введение................................................................................................................ |
.4 |
2 |
Ход работы............................................................................................................. |
5 |
|
Заключение............................................................................................................. |
9 |
|
Приложение А...................................................................................................... |
10 |
3
1Введение
Целью работы является реализация программы для работы с графами, представляющими систему дорог с переменным числом узлов и рёбер. Программа позволяет вводить графы случайным образом или с клавиатуры и выводить матрицу смежности или весов. Основное внимание уделяется нахождению города с максимальной суммой кратчайших расстояний до остальных городов.
4

2Ход работы
Вработе реализуется ориентированный граф и матрица смежности.
Ориентированный граф — В ориентированном графе рёбра имеют направление, что означает, что если есть ребро от узла A к узлу B, то это не подразумевает наличие ребра от B к A.
Матрица смежности — это квадратная матрица, которая используется для представления графа. Если граф содержит N узлов, матрица будет размером NxN.
Graph – инициализирует граф с заданным количеством городов, проверяет, чтобы количество городов было больше нуля, создает матрицу смежности, устанавливая расстояние между городами на 0 для одного и того же города и на очень большое значение для всех остальных пар. (рис .1)
Рисунок 1 — Graph
5
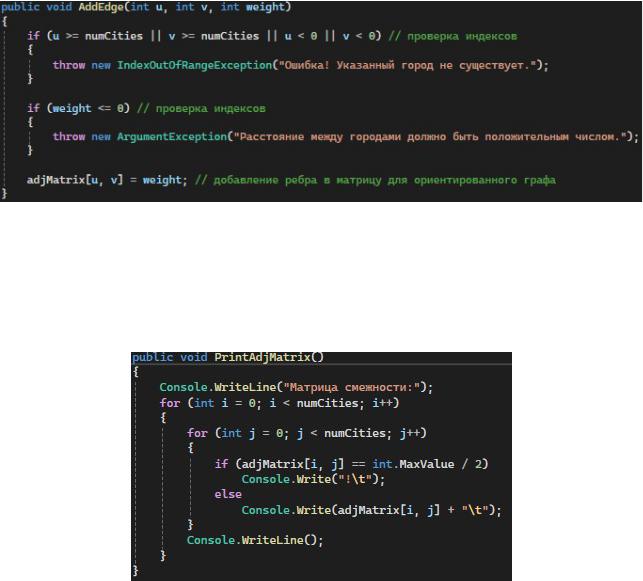
AddEdge – добавляет ребро между двумя городами с заданным весом, проверяет корректность индексов и положительность веса, устанавливает расстояние в матрице смежности для ориентированного графа (рис. 2)
Рисунок 2 — AddEdge
PrintAdjMatrix — выводит матрицу смежности на экран (рис. 3)
Рисунок 3 — PrintAdjMatrix
FloydWarshall – реализует алгоритм Флойда-Уоршелла для нахождения кратчайших расстояний между всеми парами городов, создаёт новую матрицу расстояний, копируя данные из матрицы смежности и обновляя значения, если
обнаруживаются более короткие пути через промежуточные города (рис. 4) 6

Рисунок 4 — FloydWarshall
FindCityWithMaxTotalDistance — вычисляет город с максимальной суммой кратчайших расстояний до всех остальных, вызывает метод FloydWarshall для получения кратчайших расстояний, суммирует расстояния для каждого города и обновляет максимальные значения, если найден город с большей суммой (рис. 5)
7

Рисунок 5 — FindCityWithMaxTotalDistance
8
Заключение
В ходе работы была успешно реализована программа для анализа графов дорожной сети. Выполнены задачи по вводу, выводу и поиску города с максимальными кратчайшими расстояниями. Это может быть полезным для оптимизации транспортных маршрутов.
9
Приложение А (обязательное)
class Graph
{
private int[,] adjMatrix; private int numCities;
public Graph(int numCities)
{
if (numCities <= 0)
{
throw new ArgumentException("Количество городов должно быть больше нуля.");
}
this.numCities = numCities;
adjMatrix = new int[numCities, numCities];
for (int i = 0; i < numCities; i++) // делаем матрицу смежности
{
for (int j = 0; j < numCities; j++)
{
if (i == j) adjMatrix[i, j] = 0;
else
adjMatrix[i, j] = int.MaxValue / 2; // берем половину максимального значения, чтобы избежать переполнения
}
}
10
