Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра безопасности информационных систем (БИС)

Бинарные деревья поиска

Отчет по практической работе №5

по дисциплине «Структуры данных»

Студент гр. 733-1

_______ Сметанников Д.Е

_______

Принял:

преподаватель КИБЭВС

_______ Д.Р. Уразаев

_______

Задание

Реализовать бинарное дерево поиска при помощи динамических структур (классы). Предусмотреть следующие интерфейсные методы:

• Инициализация пустого дерева.

• Добавление элемента в дерево bool AddItem( int a) - возвращает true, если добавление прошло успешно, иначе false. Например, если такой элемент уже был в дереве - то метод вернет false.

• Удаление элемента из дерева.  bool RemoveItem(int a)

• Очистка дерева void Clear()

• Вывод дерева (используйте поиск в ширину) void Print() или string Print()

Вариант 1. Реализуйте метод, находящий самый большой элемент в дереве

Содержание

Задание 2

1 Введение 4

2 Ход работы 5

Заключение 11

Приложение А 12

1. Введение

Целью данной работы является реализация бинарного дерева поиска с использованием динамических структур (классов).

2. Ход работы

AddItem: Добавляет элемент в дерево. Если дерево пустое, элемент становится корнем, иначе вызывается рекурсивная вставка (рис. 1)

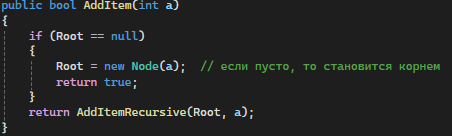
Рисунок 1 — AddItem

AddRecursive: Рекурсивно находит место для нового элемента, перемещаясь влево или вправо по дереву, в зависимости от значения элемента (рис. 2)

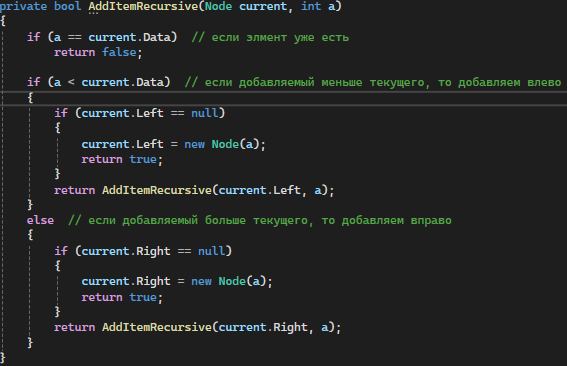
Рисунок 2 — AddRecursive

RemoveItem: Удаляет элемент из дерева. Вызывает рекурсивную функцию для поиска и удаления узла с заданным значением (рис. 3)

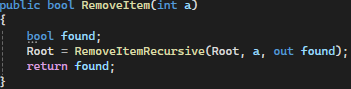
Рисунок 3 — RemoveItem

RemoveRecursive: Рекурсивно ищет элемент для удаления, перестраивая дерево в зависимости от наличия потомков у удаляемого узла (рис. 4)

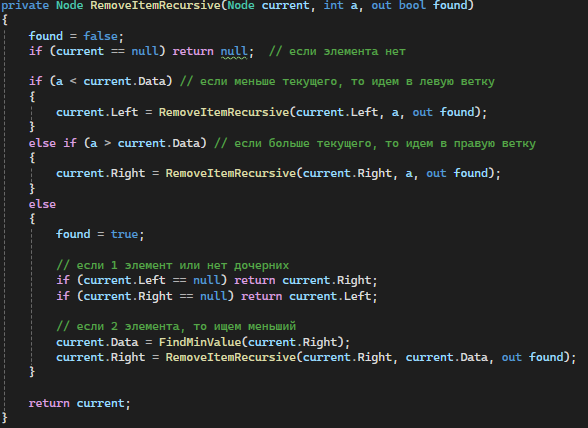
Рисунок 4 — RemoveRecursive

Clear: Очищает дерево, удаляя все узлы, сбрасывая корень дерева (рис. 5)

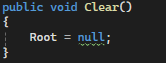
Рисунок 5 — Clear

Print: Выводит элементы дерева в ширину, начиная с корневого узла и проходя по уровням дерева (рис. 6)

Р исунок 6 — Print

FindMax: Находит и возвращает максимальный элемент дерева, проходя по правым потомкам до конца (рис. 7)

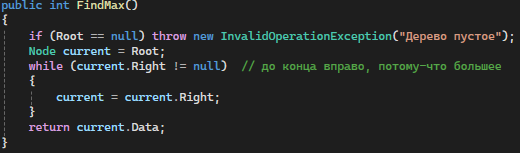
Рисунок 7 — FindMax

FindMinValue: Находит и возвращает минимальный элемент дерева. Для этого проходит по левым потомкам, начиная от корня, до самого крайнего левого узла, который и является минимальным элементом (рис. 8)

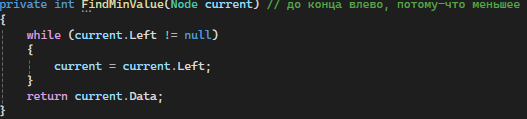
Рисунок 8 - FindMinValue

Текстовое описание реализации поиска максимального элемента дерева:

1

2

Функция поиска самого большого элемента в бинарном дереве начинается с корневого узла. Если дерево пустое, она сразу сообщает, что элементов нет. Если дерево не пустое, функция идёт по правой стороне, так как там всегда находятся элементы с большими значениями. Она продолжает двигаться вправо от узла к узлу, пока не найдёт узел, у которого нет правого "ребёнка". Этот узел и будет самым большим элементом в дереве. Как только такой узел найден, его значение возвращается как самое большое в дереве.

Текстовое описание реализации удаления элемента из дерева:

Функция удаления элемента в бинарном дереве начинается с поиска узла, который нужно удалить. Если узел найден, есть несколько вариантов. Если узел — это лист (у него нет потомков), его просто удаляют. Если у узла есть один потомок (левый или правый), узел заменяется этим потомком. Если у узла два потомка, находят наименьший элемент в правом поддереве (наименьший элемент больше удаляемого узла), копируют его значение в узел, который нужно удалить, а затем удаляют этот минимальный узел. После выполнения этих действий дерево остаётся упорядоченным (рис. 9,10,11)

Р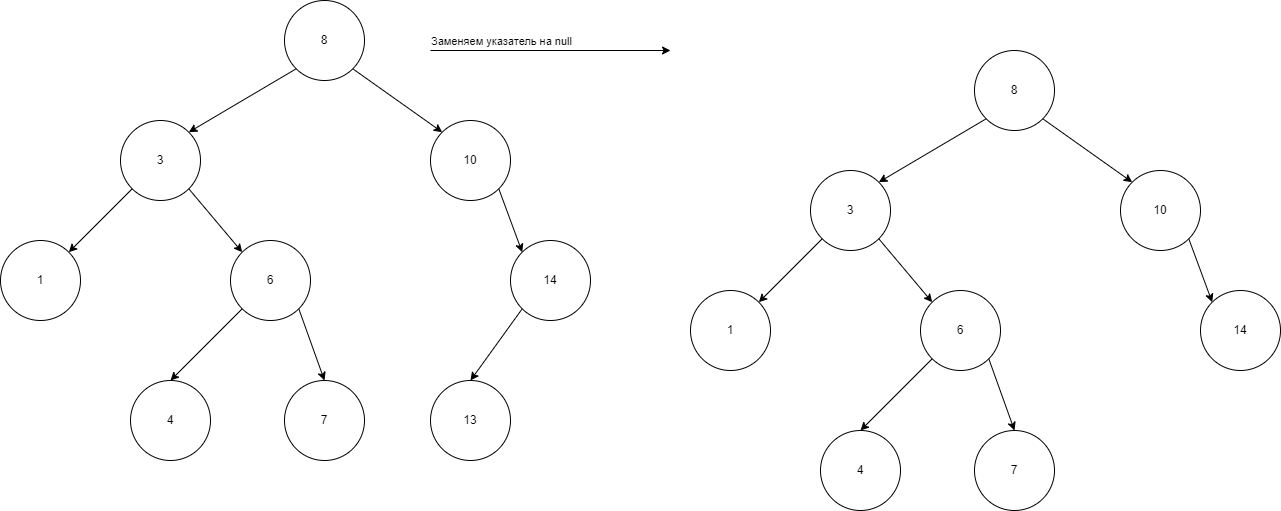 исунок 9 — Удаление листа

Р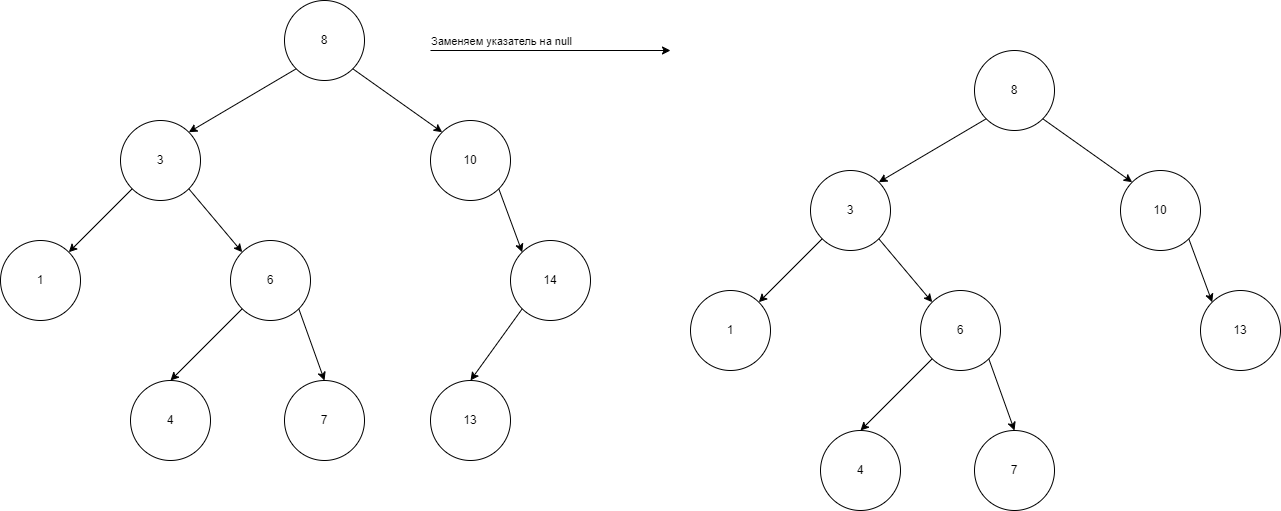 исунок 10 — Удаление с 1 поддеревом

Рисунок 11 — Удаление с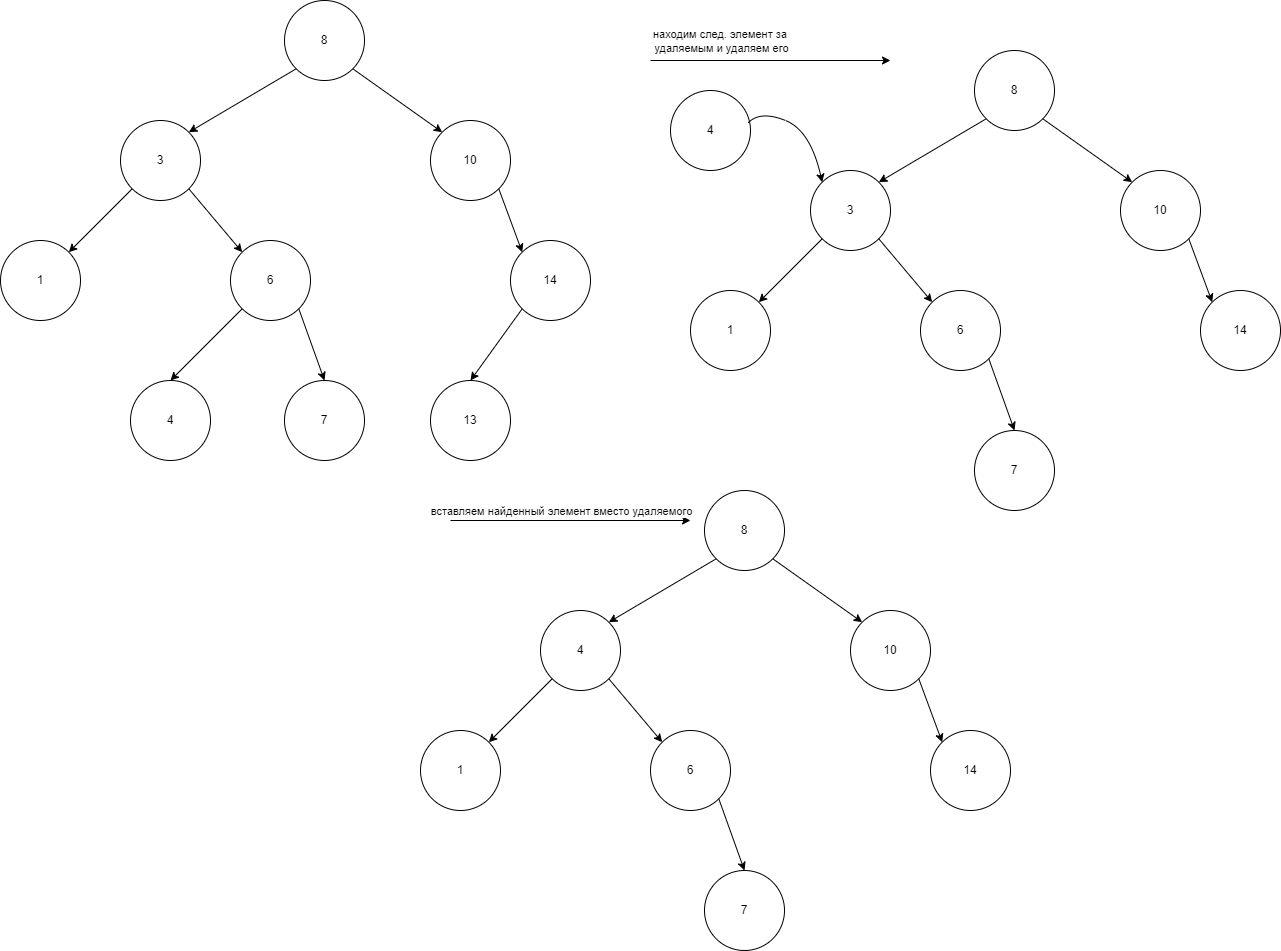 2 поддеревьями