Лаба 4 / Моделирование_в_ЭТ_Лабораторная_работа_№4_Токарев_0421

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РАПС

отчет

по лабораторной работе №4

по дисциплине «Моделирование в электротехнике»

ТЕМА: «Исследование трехфазного мостового управляемого выпрямителя в режимах выпрямления и инвертирования»

Студент гр. 0421		Токарев А.А.
Преподаватель		Армашев А.А.

Санкт-Петербург

2024

Цель работы: Исследование трехфазного мостового управляемого выпрямителя при работе на активно-индуктивную нагрузку с противо-эдс в режиме выпрямления и инвертирования. Исследование внешней, регулировочной и энергетических характеристик. Определение гармонического состава тока потребления трехфазного управляемого выпрямителя и тока, генерируемого инвертором в сеть.

Основные теоретические сведения

Трехфазная мостовая схема, представленная на рисунке 1, получила преимущественное применение при построении управляемых выпрямителей трехфазного тока.

Рисунок 1 – Схема установки

При активно-индуктивной нагрузке ток в цепи нагрузки получается идеально сглаженным и непрерывным практически во всем диапазоне регулирования (рисунок 2). При α > 30, кривая напряжения на тиристоре (U_­т) имеет отрицательные значения. Это объясняется возможностью тиристора пропускать ток при отрицательном напряжении на обмотке данной фазы за счет накопленной энергии в магнитном поле индуктивности нагрузки.

Рисунок 2 – Ток и напряжения на выпрямителе

Для трехфазного управляемого выпрямителя, выражение среднего выходного напряжения на холостом ходу (U_ср), при непрерывном токе и α < 60, определяется как:

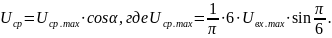
При работе управляемых выпрямителей с α = 90° и достаточной индуктивности в цепи нагрузки U_ср = 0. При 90° < α <180° в соответствии с приведенным выше выражением это напряжение должно сменить знак.

Отрицательное напряжение U_ср не в состоянии создать ток в нагрузке, так как вентили им запираются. Положение меняется, если нагрузка имеет собственный источник э.д.с. Если э.д.с. имеет полярность, совпадающую с выходным напряжением управляемого выпрямителя, то на участке 90° < α <180° ток принимает значение:

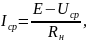
то есть ток протекает под действием э.д.с. нагрузки, преодолевая U_ср выпрямителя.

Таким образом, вентили остаются открытыми, так как ток в них течет в проводящем направлении, а энергия передается от нагрузки в сеть.

Условия, при которых такой режим может быть реализован, следующие:

• в нагрузке должна быть включена большая индуктивность;

• должен отсутствовать обратный диод;

• э.д.с. нагрузки должна быть направлена согласно с направлением напряжения на выходе выпрямителя.

Режим работы управляемого выпрямителя, когда ток нагрузки протекает навстречу выпрямленному напряжению под действием э.д.с. называется инверторным, а инвертированием называют процесс преобразования энергии постоянного тока в энергию переменного тока.

Запирание ранее проводившего тиристора при отпирании очередного тиристора в ведомом инверторе осуществляется под действием обратного напряжения, создаваемого напряжением сети со стороны вторичных обмоток трансформатора (чем и обуславливается название инвертора – «ведомый сетью»). При этом управляемый выпрямитель отрицательно влияет на питающую сеть переменного тока. Во-первых, он потребляет из сети несинусоидальный ток. Во-вторых, он сдвигает фазу потребляемого тока относительно питающего напряжения.

Соберем схему установки в Simulink. Схема установки представлена на рисунке 3.

Рисунок 3 – Схема установки в MATLAB Simulink

Параметры блоков Three-Phase Source, Three-Phase V-I Measurements, PLL (3ph), Pulse Generator (Thyristor, 6-Pulse), Universal Bridge, Series RLC Branch, Fourier I1, Fourier I0, Fourier V0, Fourier T1, RMS T представлены на рисунках 4-14.

Рисунок 4 – Параметры блока Three-Phase Source

Рисунок 5 – Параметры блока Three-Phase V-I Measurements

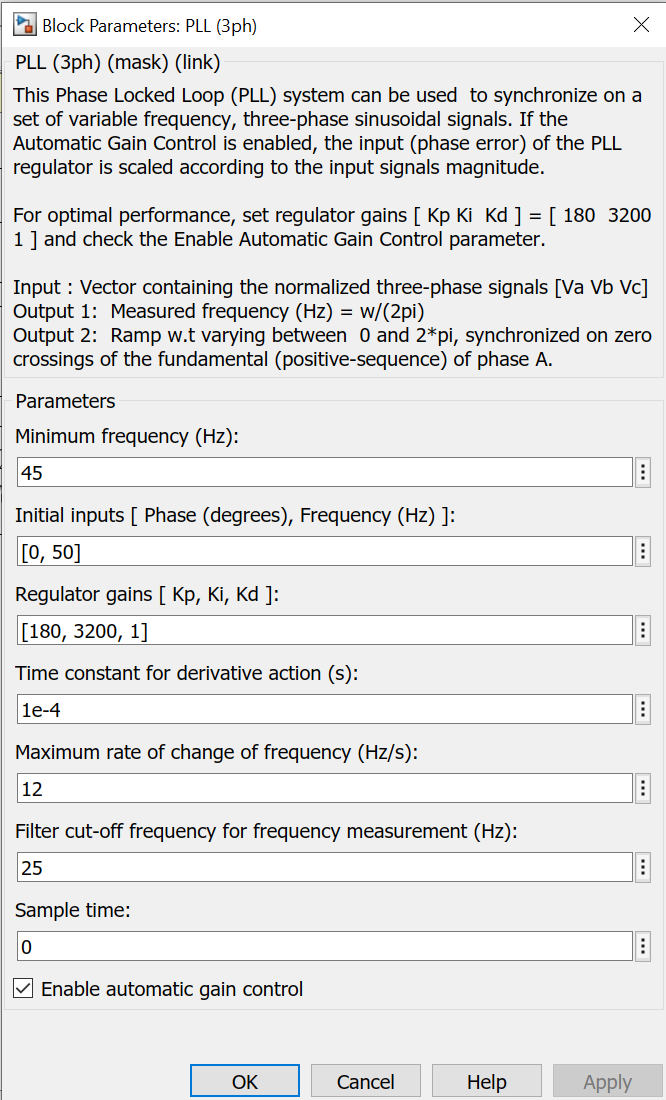
Рисунок 6 – Параметры блока PLL (3ph)

Рисунок 7 – Параметры блока Pulse Generator (Thyristor, 6-Pulse)

Рисунок 8 – Параметры блока Universal Bridge

Рисунок 9 – Параметры блока Series RLC Branch

Рисунок 10 – Параметры блока Fourier I1

Рисунок 11 – Параметры блока Fourier I0

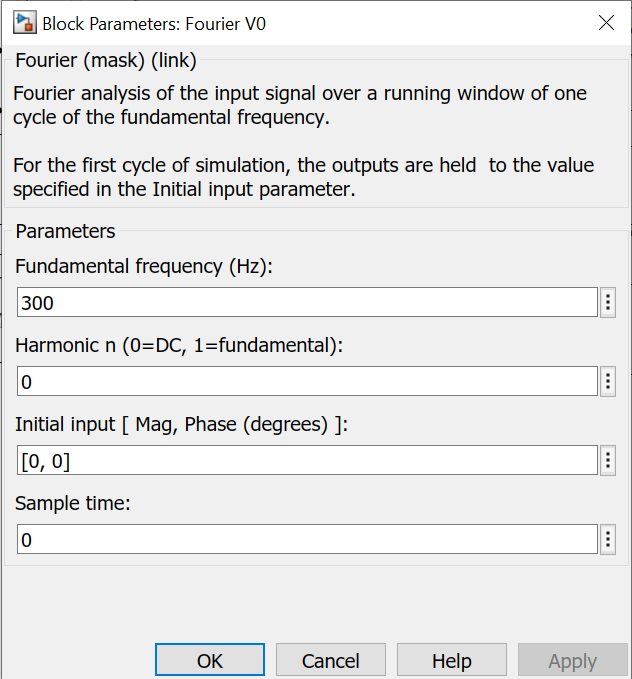
Рисунок 12 – Параметры блока Fourier V0

Рисунок 13 – Параметры блока Fourier T0

Рисунок 14 – Параметры блока RMS T

Блок To Workspace обеспечивает вывод переменной (в нашем случае тока источника) в рабочее пространство MATLAB. Параметры блока To Workspace представлены на рисунке 15.

Рисунок 15 – Параметры блока To Workspace

Изменяя противо-эдс нагрузки от -100 В до 0 В с шагом 20 В, измерим и рассчитаем основные характеристики выпрямителя. Внешние характеристики снимем при трех значениях угла управления (α = 0°, 40°, 60°). Результаты моделирования занесем в таблицу 1.

Таблица 1 – Результаты моделирования

Данные		Измерения
α	E		Iн	U­н	I1(1)max	φ1	IT0	IT	UTmax	ITmax
Град	В		А	В	А	Град	А	А	В	А
0	-100		34,21	442,5	37,73	-0,93	11,4	19,66	105,1	34,24
	-80		35,88	439,2	39,56	-0,98	11,96	20,61	115,1	35,91
	-60		37,55	435,9	41,4	-1,02	12,51	21,56	125,1	37,57
	-40		39,22	432,6	43,23	-1,06	13,07	22,51	135,1	39,24
	-20		40,88	429,3	45,07	-1,11	13,63	23,46	145,1	40,91
	0		42,55	426,0	46,91	-1,15	14,18	24,41	155,1	42,57
40	-100		24,21	342,5	26,7	-39,96	8,07	13,98	436,9	24,31
	-80		25,87	339,2	28,53	-39,96	8,62	14,94	456,9	25,97
	-60		27,54	335,9	30,37	-39,96	9,18	15,9	476,9	27,64
	-40		29,2	332,4	32,20	-39,96	9,733	16,86	496,9	29,30
	-20		30,86	329	34,04	-39,96	10,29	17,82	516,9	30,96
	0		32,53	325,8	35,87	-39,96	10,84	18,78	536,9	32,63
60	-100		13,45	234,7	14,84	-59,95	4,49	7,77	479,6	13,59
	-80		15,27	232,9	16,58	-59,95	5,09	8,82	481,4	15,41
	-60		16,19	222,3	17,86	-59,95	5,40	9,35	482,3	16,33
	-40		17,85	218,9	19,69	-59,95	5,95	10,31	496,9	17,99
	-20		19,52	215,6	21,53	-59,95	6,51	11,27	516,9	19,66
	0		21,18	212,3	23,36	-59,95	7,06	12,23	536,9	21,32

Полная мощность, потребляемая выпрямителем от источника питания по первой гармонике:

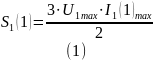
Активная мощность, потребляемая выпрямителем от источника питания по первой гармонике:

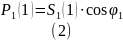
Мощность в нагрузке:

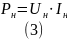
Потери в тиристоре:

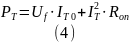
Рассчитаем полную и активную мощность, потребляемую выпрямителем от источника питания по первой гармонике, а также мощность в нагрузке и потери в тиристоре, согласно формулам (1) – (4). В качестве примера расчета приведем первое измерение.

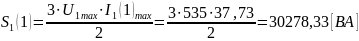
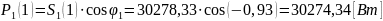
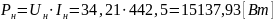
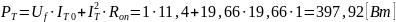
Рассчитаем полную и активную мощность, потребляемую выпрямителем от источника питания по первой гармонике, а также мощность в нагрузке и потери в тиристоре для остальных измерений. Полученные результаты занесем в таблицу 2.

Таблица 2 – Результаты вычислений

Данные			Вычисления
α	E	S1(1)		P1(1)	Pн	PТ
Град	В	ВА		Вт	Вт	Вт
0	-100	30278,33		30274,34	15137,93	397,92
	-80	31746,90		31742,26	15758,50	436,73
	-60	33223,50		33218,24	16368,05	477,34
	-40	34692,08		34686,14	16966,57	519,77
	-20	36168,68		36161,89	17549,78	564,00
	0	37645,28		37637,69	18126,30	610,03
40	-100	21426,75		16423,45	8291,93	203,51
	-80	22895,33		17549,11	8775,10	231,82
	-60	24371,93		18680,91	9250,69	261,99
	-40	25840,50		19806,56	9706,08	293,99
	-20	27317,10		20938,37	10152,94	327,84
	0	28785,68		22064,02	10598,27	363,53
60	-100	11909,10		5963,55	3156,72	64,86
	-80	13305,45		6662,78	3556,38	82,88
	-60	14332,65		7177,15	3599,04	92,82
	-40	15801,23		7912,55	3907,37	112,25
	-20	17277,83		8651,97	4208,51	133,52
	0	18746,40		9387,36	4496,51	156,63

По данным таблиц 1и 2 построим внешние (нагрузочные характеристики) характеристики управляемого выпрямителя U_н = f(I_н), а также энергетические характеристики выпрямителя S₁(1) = f(P_н), P₁(1) = f(P_н), P_T = f(P_н), I₁(1)_max = f(I_н), I_T0 = f(I_н), I_T = f(I_н) при различных углах управления α. В случае, когда характеристики находятся далеко друг от друга на плоскости координат, аппроксимируем их для того, чтобы была возможность их сравнения. Характеристики представлены на рисунках 16-22.

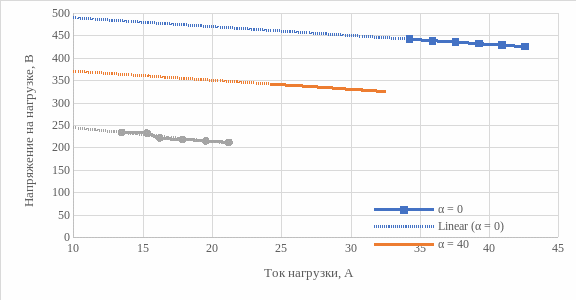
Рисунок 16 – Внешние характеристики выпрямителя

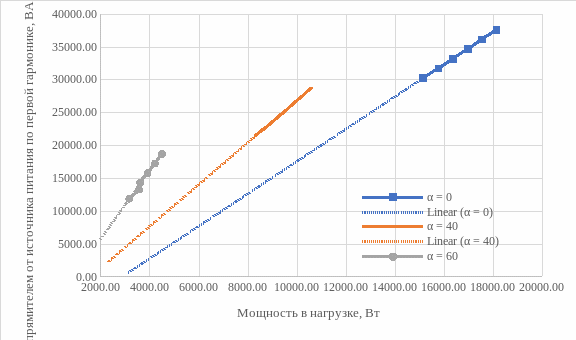
Рисунок 17 – Энергетические характеристики выпрямителя S₁(1) = f(P_н)

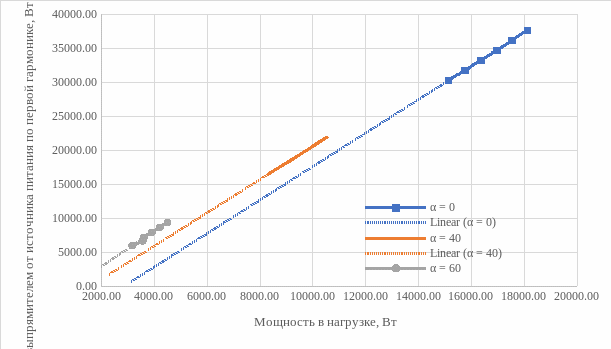
Рисунок 18 – Энергетические характеристики выпрямителя P₁(1) = f(P_н)

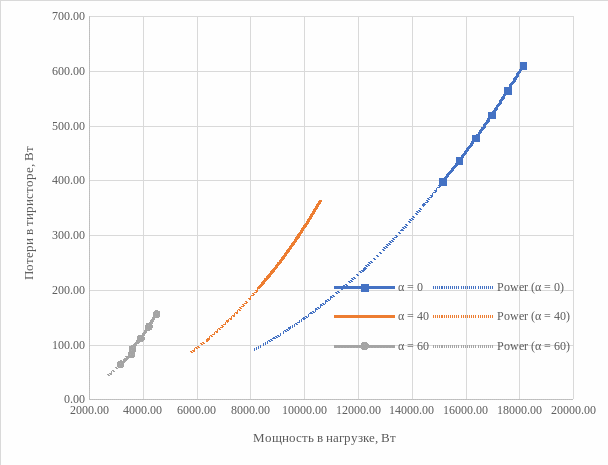
Рисунок 19 – Энергетические характеристики выпрямителя P_Т = f(P_н)

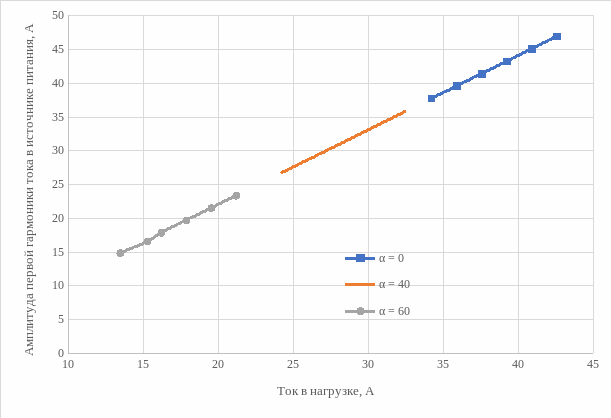
Рисунок 20 – Энергетические характеристики выпрямителя I₁(1)_max = f(I_н)

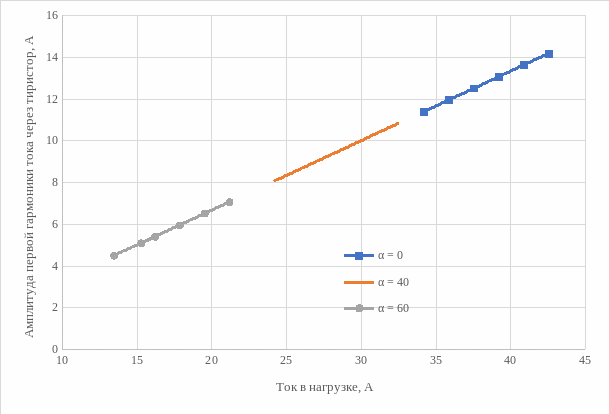
Рисунок 21 – Энергетические характеристики выпрямителя I_Т0 = f(I_н)

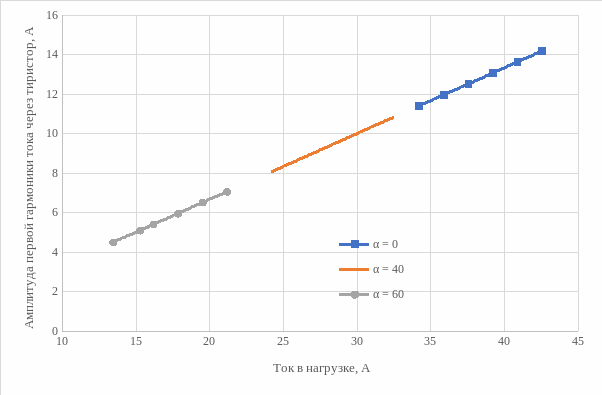
Рисунок 22 – Энергетические характеристики выпрямителя I_Т = f(I_н)

Исследуем регулировочную характеристику однофазного управляемого выпрямителя при значении противо-эдс, равном -20 В и изменении угла управления от 0 до 120 градусов с шагом 20 градусов. Результаты измерений занесем в таблицу 3.

Таблица 3 – Результаты моделирования регулировочной характеристики

Измерения
α (град)	Uн (В)
0	429,3
20	403
40	329
60	215,6
80	75,92
100	20,03
120	20,01

По данным таблицы 3 построим регулировочную характеристику выпрямителя U_н = f(α). Регулировочная характеристика представлена на рисунке 23.

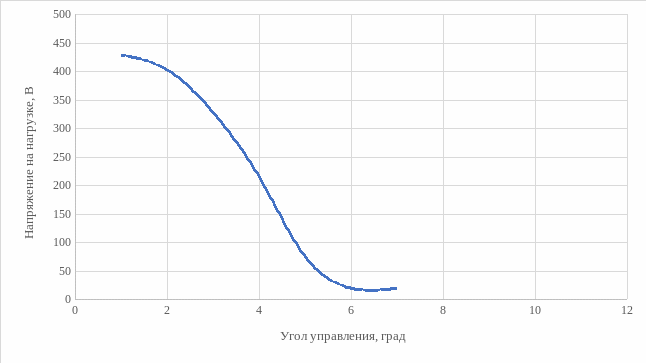
Рисунок 23 – Регулировочная характеристика выпрямителя

Исследуем спектральный состав тока, потребляемого управляемым выпрямителем в пакете расширения Signal Processing Toolbox. Используя средства просмотра сигнала, записанного в рабочую область MATLAB под именем Lab_4, просмотрим исследуемый сигнал. Выбор искомого сигнала представлен на рисунке 24.

Рисунок 24 – Выбор сигнала Lab_4 в окне анализа сигнала

Спектр сигнала Lab_4 представлен на рисунке 25.

Рисунок 25 – Спектр тока источника

Исследуем гармонический состав тока, потребляемого управляемым выпрямителем при значении угла управления α = 40º. Измерим значения y­₁ – y₅ со спектра, а также значение I₁(1)_max с лабораторной установки. Полученные результаты занесем в таблицу 4.

Таблица 4 – Спектральный состав потребляемого тока

Измерения
α (град)	y1	y2	y3	y4	y5	I1(1)max (A)
40	50	6,19	3,39	1,21	0,53	34,04

Для определения абсолютных гармонических составляющих в амперах воспользуемся следующей формулой:

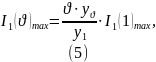
где ϑ – номер гармоники, I₁(ϑ)_max – амплитуда тока ϑ-той гармоники в амперах, y₁, y_ϑ – значения, определенные путем спектрального анализа, I₁(1)_max – ток, считанный с дисплея в амперах. Рассчитаем абсолютные гармонические составляющие тока, потребляемого выпрямителем, согласно формуле (5). В качестве примера приведем вторую гармонику:

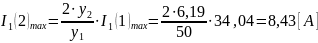
Аналогичным образом рассчитаем значения всех остальных гармонических составляющих. Результаты занесем в таблицу 5.

Таблица 5 – Результаты расчетов абсолютных гармонических составляющих

Вычисления
I1(2)max (A)	I1(3)max (A)	I1(4)max (A)	I1(5)max (A)
8,43	4,62	1,65	0,72

Исследуем регулировочную и энергетическую характеристики ведомого сетью инвертора. Характеристики снимем для трех значений противо-эдс: 200 В, 300 В и 400 В. При этом, угол управления α будем изменять от 90º до 110º с шагом в 10º. Результаты моделирования занесем в таблицу 6.

Таблица 6 – Результаты моделирования

Данные		Измерения
α	E	Iн	U­н	I1(1)max	φ1	UTmax	ITmax
Град	В	А	В	А	Град	В	А
90	200	16,48	34,99	18,17	-89,93	736,5	16,64
	300	24,81	51,65	27,35	-89,93	836,5	24,96
	400	33,13	68,31	36,53	-89,91	936,5	33,28
100	200	9,07	109,2	9,99	-99,92	547,5	9,22
	300	17,39	125,8	19,17	-99,93	555,8	17,54
	400	25,72	142,4	28,35	-99,92	564,1	25,86
110	200	0,008	199,99	0,009	-33,67	698,9	0,002
	300	10,2	197,9	11,24	-109,9	548,8	10,34
	400	18,52	214,5	20,41	-109,9	557,1	18,66