МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РАПС

отчет

по самостоятельной работе №2

по дисциплине «Электронные и электрические аппараты»

Тема: «Электромагнитные механизмы переменного тока»

Студент гр. 0421		Токарев А.А.
Преподаватель		Сепп Ю.И.

Санкт-Петербург

2023

Содержание

1. Электромагнитный механизм с двухфазной системой питания переменным током 3

1.1 Исходные данные 3

1.2 Задача 1.1 3

1.3 Задача 1.2. 5

1.4 Задача 1.3.1 8

1.5 Задача 1.3.2 9

1.6 Задача 1.3.3 9

1.7 Задача 1.3.4 10

2 Задача 2. Электромагнитный механизм с трехфазной системой питания переменным током 12

2.1 Исходные данные 12

2.2 Задача 2.1 12

2.3 Задача 2.2. 15

2.4 Задача 2.3.1 18

2.5 Задача 2.3.2 20

3 Задача 3. Потребляемая электромагнитным механизмом реактивная мощность 21

4 Задача 4. Дополнительные вопросы 25

4.1 Задача 4.1 25

4.2 Задача 4.2 27

5 Список используемой литературы 35

1. Электромагнитный механизм с двухфазной системой питания переменным током

1.1 Исходные данные

Рассматриваются электромагнитный механизм и связная система его питания с пронумерованной последовательностью чередования фаз, представленные на рисунке 1. Пусть напряжения на зажимах фаз равны U₁ = U₁(t) и U₂ = U₂(t) и определяются известным образом.

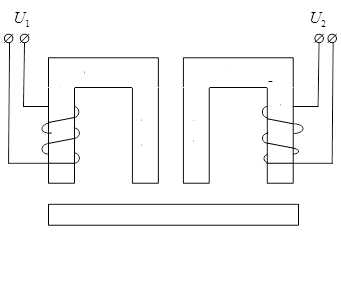
Рисунок 1 – Эскиз электромагнитного механизма

1.2 Задача 1.1

Определить, как это принято, параметры системы питания.

Решение:

При анализе мгновенных значения динамических параметров состояния в установившихся режимах устанавливаются следующие допущения:

1. Исходим из принципа суперпозиции.

2. Состояния магнитной и электрической подсистем ЭМП аппарата рассматриваем как суперпозицию гармонических состояний, мгновенные значения параметров которых для указанных подсистем имеют вид:

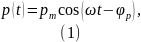
где p_m – вещественнозначное амплитудное значение параметра p для участвующего в указанной суперпозиции элементарного «чистого» состояния;

ω = 2πf – круговая частота параметра p;

f = 1/T – циклическая частота изменения параметра p;

T – характерное время изменения параметра p, период;

φ_p – начальная фаза, определяющая значение данного параметра в момент времени t = 0;

Для придания определенности изменениям значений рассматриваемых параметров в принятой к рассмотрению системе отсчета времени будем считать, как это принято, что знак «минус» в определении временной фазы фиксирован и всегда φ_p ≥ 0.

3. Изменяющиеся во времени состояния считаем удовлетворяющими условиям квазистационарности, а процессы перехода из одного состояния в другое рассматриваем как квазистатические, для которых всегда справедливо уравнение баланса напряжений:

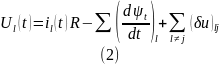
4. Считаем, что между намагничивающей силой и магнитным потоком имеет место прямая пропорциональная зависимость (закон Ома):

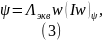
где 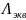– расчетное значение магнитной проводимости, эквивалентное по полному потокосцеплению обмотки;

w – число витков обмотки;

Исходя из принятых выше допущений и линейности выражения (2), определим параметры двухфазной системы питания:

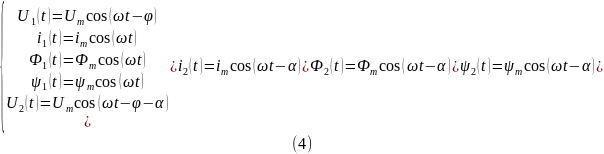
Подставим выражения для первой фазы в (2):

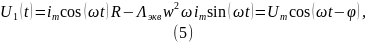
где

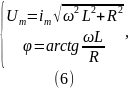
где 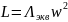– индуктивность цепи обмотки.

При допущении, что в рассматриваемой цепи ωL >> R:

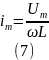
а также, при учете (3):

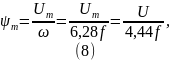
т.к. .

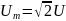Аналогичные выражения для амплитудных значений можно получить и для второй фазы питания. Тогда параметры системы питания, выраженные через напряжение питания и конструктивные параметры электромагнитного механизма, будут равны:

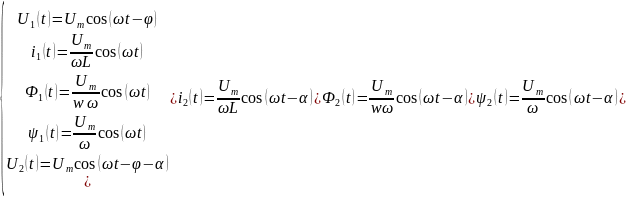
1.3 Задача 1.2.

Какие механические характеристики (параметры) определяют изменения механического состояния якоря в любой момент времени? Определить необходимые параметры.

Решение:

Изменение механического состояния якоря в любой момент времени определяются двумя механическими характеристиками – тяговым усилием и моментом сил тягового усилия. Выберем для рассмотрения правую систему координат, связанную с неподвижным сердечником механизма с направлением оси Ох вдоль длины воздушного зазора. Эскиз электромагнитного механизма представлен на рисунке 2.

n₃

n₂

M₄

M₃

M₂

M₁

r₁

r₂

r₄

r₃

F

n₄

n₁

σ⁴

σ³

σ²

σ¹

F₄

F₃

F₂

F₁

0

Х

Ф₂

Ф₁

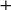
Рисунок 2 – Эскиз электромагнитного механизма с указанием сил и моментов сил, действующих на механизм

Пренебрегая выпучиванием магнитных линий из воздушных зазоров, считая магнитное поле в зазорах однородным, находим, что индукция в зазорах электромагнита направлена вдоль оси Ох, т.е. в зазорах от нуля отличны только составляющие индукции:

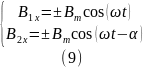
Отсюда следует, что среди компонентов тензора напряжений в любом из зазоров отличным от нуля является только:

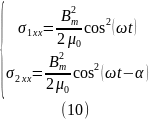
Поэтому, среди компонентов векторов напряжений σ^1,2 и σ^3,4 к поверхностям границ между якорем и зазорами 1 и 2, а также между якорем и зазорами 3 и 4 отличными от нуля будут только составляющие вдоль оси Х, т.е. σ^1,2 = (σ_1xx, 0, 0) и σ^3,4 = (σ_2xx, 0, 0). Тогда, учитывая направление векторов единичной нормали n к рассматриваемым граничным поверхностям, согласно определению, находим, что потоки механического импульса, поступающие из соответственных зазоров в якорь, равны:

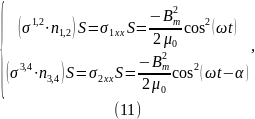
где S – площади поверхностей якоря, граничащих с зазорами (площади поперечных сечений зазоров).

Пользуясь принципом Сен-Венана, связываем с поступающими в якорь потоками механического импульса ньютоновы силы F_1,2 и F_3,4, равные по величине механическим импульсам, поступающим за единицу времени в якорь со стороны соответственных воздушных зазоров:

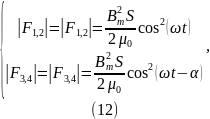
имеющим направление вектора плотности потока импульса и точки приложения, совпадающие с центрами масс участков, непосредственно примыкающих к его поверхностям, воспринимающих указанные и обозначенные потоки.

После того, как мы определили параметры механического воздействия магнитного поля, формируемого в воздушных зазорах рассматриваемого электромагнитного механизма, проанализируем изменения механического состояния якоря с позиций механики. При этом якорь будем рассматривать, как абсолютно твердое тело с действующими на него силами, приложенными к разным его точкам. При определении результирующего (от совместного действия выделенных ньютоновых сил) воздействия магнитного поля на якорь, согласно принципам теоретической механики, нам необходимо привести все действующие на него силы к центру масс якоря, осуществить векторное сложение сил, а также определить и сложить моменты рассматриваемых сил относительно указанного центра приведения.

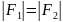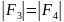Так как в любой момент времени , а , то результирующий момент, определяемый как:

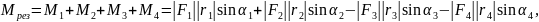
где r₁, r₂, r₃, r₄ – радиус-векторы, направленные от точек приложения сил F₁ – F₄ к центру масс электромагнитного механизма;

α₁, α₂, α₃, α₄ – углы между радиус-векторами r₁ – r₄ и векторами сил F₁ – F₄;

будет равен нулю, а результирующая сила, прилагаемая к указанному центру масс, будет равна по величине:

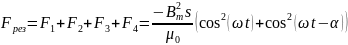
и направлена в направлении вектора плотности потока механического импульса.

Осуществляя очевидное преобразование, для величины результирующего усилия находим:

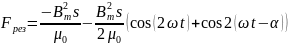
Постоянный член в этом выражении представляет собой среднее за период значение усилия, совершающего полезную работу. Со вторым членом связано изменяющееся во времени воздействие, приводящее к вибрации в рассматриваемом электромагнитном механизме.