МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РАПС

отчет

по самостоятельной работе №1

по дисциплине «Электронные и электрические аппараты»

Тема: «Расчет параметров магнитной цепи аппарата»

Студент гр. 0421		Токарев А.А.
Преподаватель		Сепп Ю.И.

Санкт-Петербург

2023

Содержание

1 Задача 1 3

1.1 Исходные данные 3

1.2 Этап 1. Разбиение на участки 3

1.2.1 Задача 1.1. Выделение, обоснование и нумерация в конструктивном объеме замкнутых контуров, к которым будет применяться закон полного тока. Выбор системы координат путем задания положительного направления обхода выделенных контуров. 3

1.2.2 Задача 1.2. Определение и нумерация на каждом из выделенных контуров участков, соответствующих конструктивным элементам с разными геометрическими параметрами и различными значениями материальных констант, а также фиксация границ указанных участков для четкого определения их длин из заданных чертежей. 4

1.2.3 Задача 1.3. Спецификация геометрических параметров определенных участков каждого выделенного контура с указанием численных значений материальных констант, необходимых для последующих расчетов. 6

1.3 Этап 2. Формирование схемы замещения рассматриваемого устройства 8

1.4 Этап 3. Формулировка уравнений состояния рассматриваемой магнитной цепи 9

1.5 Этап 4. Решение уравнений состояния и получение решения поставленной задачи 10

1.5.1 Задача 1.1 10

1.5.2 Задача 1.2 11

1.5.3 Задача 1.3 12

2 Задача 2 14

2.1 Исходные данные 14

2.2 Этап 1. Разбиение на участки 15

2.2.1 Задача 1.1. Выделение, обоснование и нумерация в конструктивном объеме замкнутых контуров, к которым будет применяться закон полного тока. Выбор системы координат путем задания положительного направления обхода выделенных контуров. 15

2.2.2 Задача 1.2. Определение и нумерация на каждом из выделенных контуров участков, соответствующих конструктивным элементам с разными геометрическими параметрами и различными значениями материальных констант, а также фиксация границ указанных участков для четкого определения их длин из заданных чертежей. 16

2.2.3 Задача 1.3. Спецификация геометрических параметров определенных участков каждого выделенного контура с указанием численных значений материальных констант, необходимых для последующих расчетов. 18

2.3 Этап 2. Формирование схемы замещения рассматриваемого устройства 19

2.4 Этап 3. Формулировка уравнений состояния рассматриваемой магнитной цепи 20

2.5 Этап 4. Решение уравнений состояния и получение решения поставленной задачи 21

2.5.1 Задача 2.1 21

2.5.2 Задача 2.2 22

2.5.3 Задача 2.3 26

3 Список используемой литературы 27

1 Задача 1

1.1 Исходные данные

Рассматривается П-образный электромагнит постоянного тока с внешним поперечно двигающимся якорем. Эскиз электромагнита представлен на рисунке 1.

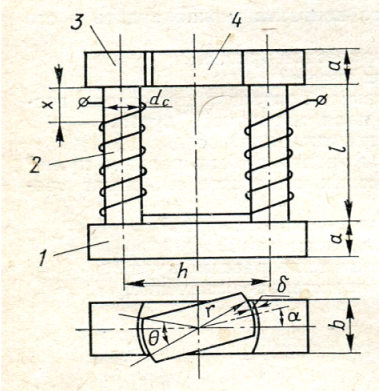
Рисунок 1 – Эскиз электромагнита

На рисунке 1 части электромагнита обозначаются следующим образом: 1 – основание, 2 – сердечник, 3 – полюсный наконечник, 4 – якорь. Размеры электромагнита: a = 2,0∙10^-2 м, b = 2,0∙10^-2 м, d_c = 1,5∙10^-2 м, r = 2,0∙10^-2 м, l = 6,0∙10^-2 м, h = 6,0∙10^-2 м, δ = 1,0∙10^-4 м.

1.2 Этап 1. Разбиение на участки

1.2.1 Задача 1.1. Выделение, обоснование и нумерация в конструктивном объеме замкнутых контуров, к которым будет применяться закон полного тока. Выбор системы координат путем задания положительного направления обхода выделенных контуров.

Выделим в конструктивном объеме замкнутые контуры, к которым будет применяться закон полного тока:

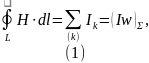
где H = H (r, t) – напряженность магнитного поля в пространственной точке r в момент времени t, L – замкнутый контур, охватываемый систему токов I_k, с которым связывается падение магнитного потенциала (Iw)_Σ­ (магнитодвижущая сила или м.д.с.) при перемещении по контуру L.

Так как применение закона (1) не зависит от положения выбираемого контура относительно геометрических центров поперечных сечений, через которые контур проходит, то для удобства рассмотрения контур выбирается проходящим через указанные центры. Выберем такую систему координат, что её начало отсчета будет связано с основанием электромагнита, ось Ох направим вверх относительно основания. Положительное направление обхода контура выберем по положительному направлению вектора плотности магнитного потока B, которое, в свою очередь, определяется по правилу буравчика из выбранного направления вектора плотности тока j.

1.2.2 Задача 1.2. Определение и нумерация на каждом из выделенных контуров участков, соответствующих конструктивным элементам с разными геометрическими параметрами и различными значениями материальных констант, а также фиксация границ указанных участков для четкого определения их длин из заданных чертежей.

Пронумеруем каждый из участков на выделенных контурах. Необходимо учесть, что на таких участках, как А₁₂А₁ и А₁А₂ изменяется только направление передачи магнитного потока без изменения величины падения магнитного потенциала на указанных участках, т.к. передача магнитного потока происходит через все поперечное сечение конструктивного элемента на выбранных участках. Поэтому можно пренебречь участком А₁₂А₁. Аналогично можно пренебречь участками А₆А₇, А_8­А₉ и А₁₀А₁₁. Эскиз с выделением контуров и маркировкой участков представлен на рисунке 2.

Рисунок 2 – Эскиз электромагнита с выделением контуров и маркировкой отдельных участков

1.2.3 Задача 1.3. Спецификация геометрических параметров определенных участков каждого выделенного контура с указанием численных значений материальных констант, необходимых для последующих расчетов.

В данном случае в состав формируемой магнитной цепи входит один ориентированный контур, состоящий из следующих участков:

участок А₁А₂ имеет длину

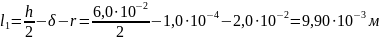
и площадь поперечного сечения

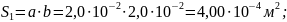
материал Сталь10 – кривая намагничивания представлена на рисунке 4

участок А₂А₃ имеет длину

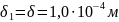
Так как зазор мал по сравнению с другими геометрическими размерами, то его поперечное сечение можно рассматривать как плоское с площадью, учитывающее кривизну воспринимающей поверхности, а также можно пренебречь разницей в площадях поверхности, передающей в зазор магнитный поток и поверхности, воспринимающей магнитный поток с другой стороны зазора. В зависимости от угла поворота α поперечное сечение зазора S_δ изменяется и определяется как функция от угла поворота S_δ = S_δ(α).

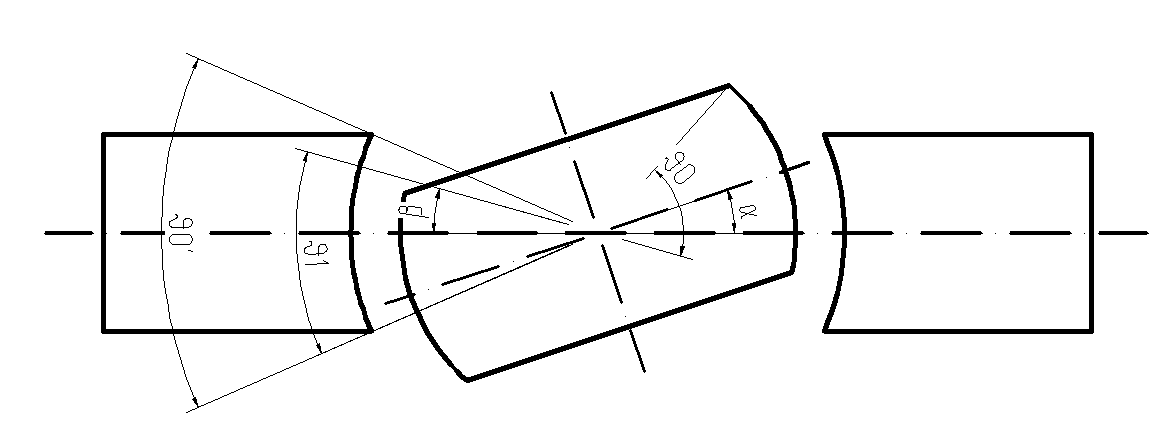
Рисунок 3 – Иллюстрация к вычислению функции зависимости площади поперечного зазора от угла поворота якоря

Найдем зависимость угла перекрытия θ₁ от угла α из геометрических соображений:

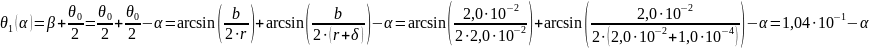
Теперь найдем зависимость площади поперечного сечения зазора от угла α:

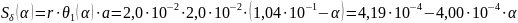
Таким образом:

площадь поперечного сечения

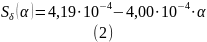
материал воздух – μ₀ = 4π∙10^-7 Гн/м

участок А₃А₄ имеет длину

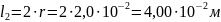
и площадь поперечного сечения

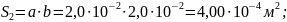
материал Сталь10 – кривая намагничивания представлена на рисунке 4

участок А₄А₅ имеет длину

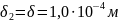
и площадь поперечного сечения из (2):

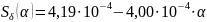
материал воздух – μ₀ = 4π∙10^-7 Гн/м

участок А₅А₆ имеет длину

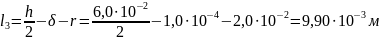
и площадь поперечного сечения

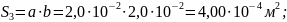
материал Сталь10 – кривая намагничивания представлена на рисунке 4

участок А₇А₈ имеет длину

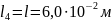
и площадь поперечного сечения

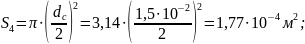
материал Сталь10 – кривая намагничивания представлена на рисунке 4

участок А₉А₁₀ имеет длину

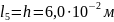
и площадь поперечного сечения

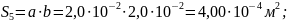
материал Сталь10 – кривая намагничивания представлена на рисунке 4

участок А₁₁А₁₂ имеет длину

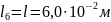
и площадь поперечного сечения

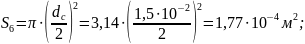
материал Сталь10 – кривая намагничивания представлена на рисунке 4

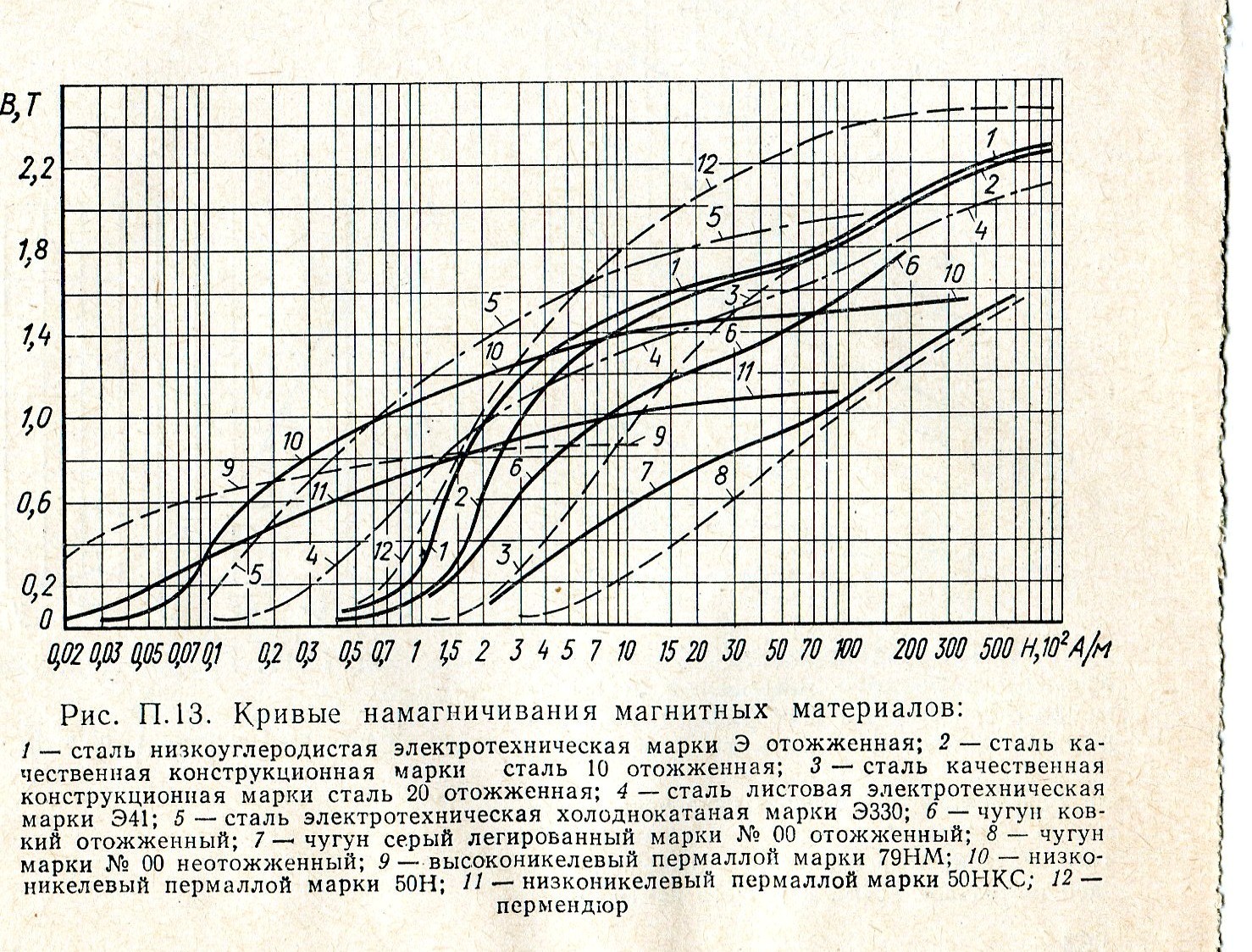
Рисунок 4 – Кривые намагничивания магнитных материалов (Сталь10 обозначена цифрой 2)