7 Вычисление реакции при воздействии одиночного импульса
7.1 Аналитический метод расчета
Найдем изображение по Лапласу входного одиночного импульса, для чего с помощью метода двойного дифференцирования представим указанный импульс в виде суммы функций. Графически метод двойного дифференцирования проиллюстрирован на рисунке 15.
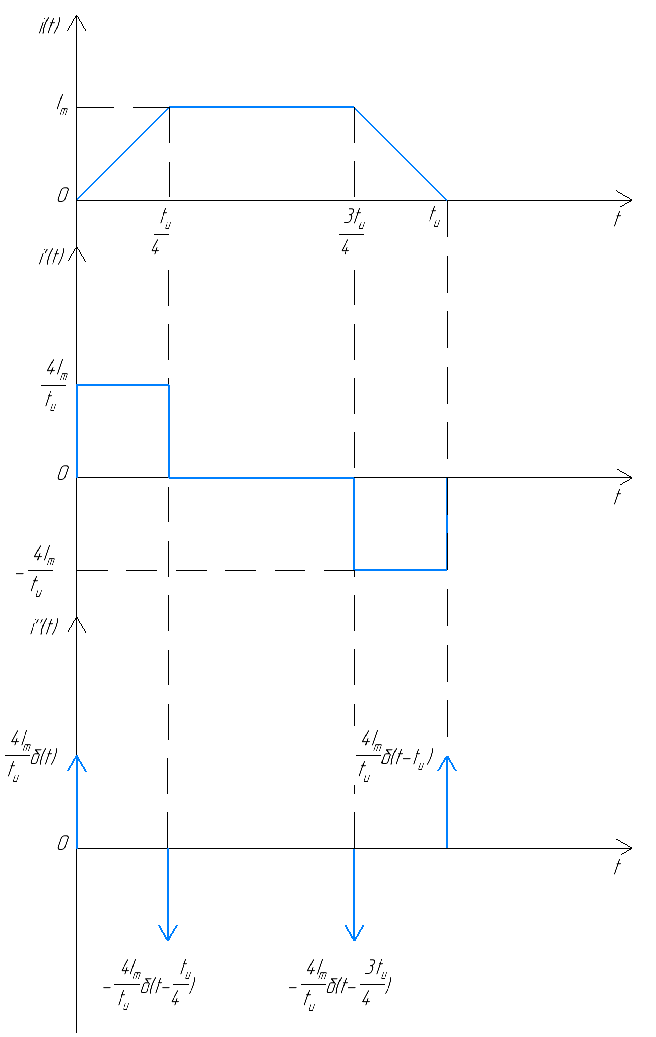
Рисунок 15 – Иллюстрация к методу двойного дифференцирования
Исходя из рисунка 15, входящий импульс можно представить в виде:
Тогда его изображение по Лапласу будет равно:
Запишем выражение для изображения реакции цепи на входной одиночный импульс:
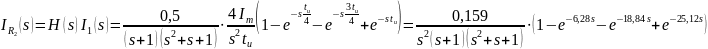
Воспользуемся теоремой разложения и разложим левую часть выражения, содержащую полином, на множители:
Таким образом:
Теперь мы можем найти
,
выполнив обратное преобразование
Лапласа для
.
Графики реакции (обозначен штриховой линией) и измененного в А(0) = 0,5 раз воздействия (обозначен сплошной линией) представлены на рисунке 16. Получившиеся кривые подтверждают правильность предположений, сделанных ранее на основе анализа частотных характеристик.
Рисунок 16 – Реакция цепи и измененное в А(0) раз воздействие цепи
7.2 Численный метод расчета
Воспользуемся уравнениями, полученными при выполнении численного расчета в пункте 5:
В качестве примера приведем первые три шага расчета. Шаг первый:
Шаг второй:
Шаг
третий:
Вычислим все значения величин на интервале от 0 до 10 секунд. Результат сведем в таблицу 3.
Таблица 3 – Результаты расчета реакции цепи явным методом Эйлера
t, c |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|
0,000 |
0,000 |
0,003 |
0,009 |
0,018 |
0,029 |
0,042 |
0,056 |
0,072 |
|
0,000 |
0,000 |
0,000 |
0,000 |
0,001 |
0,002 |
0,003 |
0,005 |
0,008 |
|
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,001 |
|
0,000 |
0,032 |
0,064 |
0,095 |
0,127 |
0,159 |
0,191 |
0,223 |
0,254 |
t, c |
0,9 |
1 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
|
0,090 |
0,108 |
0,128 |
0,148 |
0,168 |
0,189 |
0,211 |
0,232 |
0,254 |
|
0,011 |
0,016 |
0,021 |
0,027 |
0,034 |
0,042 |
0,051 |
0,061 |
0,072 |
|
0,002 |
0,003 |
0,004 |
0,006 |
0,008 |
0,010 |
0,014 |
0,017 |
0,022 |
|
0,286 |
0,318 |
0,350 |
0,382 |
0,413 |
0,445 |
0,477 |
0,509 |
0,541 |
t, c |
1,8 |
1,9 |
2 |
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
|
0,275 |
0,297 |
0,318 |
0,339 |
0,359 |
0,380 |
0,399 |
0,419 |
0,438 |
|
0,084 |
0,096 |
0,109 |
0,123 |
0,138 |
0,153 |
0,169 |
0,185 |
0,202 |
|
0,027 |
0,032 |
0,039 |
0,046 |
0,054 |
0,062 |
0,071 |
0,081 |
0,091 |
|
0,572 |
0,604 |
0,636 |
0,668 |
0,700 |
0,731 |
0,763 |
0,795 |
0,827 |
t, c |
2,7 |
2,8 |
2,9 |
3 |
3,1 |
3,2 |
3,3 |
3,4 |
3,5 |
|
0,457 |
0,475 |
0,493 |
0,510 |
0,527 |
0,544 |
0,560 |
0,576 |
0,592 |
|
0,220 |
0,237 |
0,255 |
0,274 |
0,292 |
0,311 |
0,330 |
0,349 |
0,368 |
|
0,102 |
0,114 |
0,126 |
0,139 |
0,153 |
0,167 |
0,181 |
0,196 |
0,211 |
|
0,859 |
0,890 |
0,922 |
0,954 |
0,986 |
1,018 |
1,049 |
1,081 |
1,113 |
t, c |
3,6 |
3,7 |
3,8 |
3,9 |
4 |
4,1 |
4,2 |
4,3 |
4,4 |
|
0,607 |
0,622 |
0,637 |
0,652 |
0,666 |
0,681 |
0,695 |
0,709 |
0,723 |
|
0,387 |
0,406 |
0,425 |
0,444 |
0,462 |
0,481 |
0,500 |
0,518 |
0,536 |
|
0,227 |
0,243 |
0,259 |
0,276 |
0,293 |
0,310 |
0,327 |
0,344 |
0,361 |
|
1,145 |
1,177 |
1,208 |
1,240 |
1,272 |
1,304 |
1,336 |
1,367 |
1,399 |
t, c |
4,5 |
4,6 |
4,7 |
4,8 |
4,9 |
5 |
5,1 |
5,2 |
5,3 |
|
0,737 |
0,751 |
0,765 |
0,779 |
0,793 |
0,807 |
0,821 |
0,835 |
0,849 |
|
0,554 |
0,572 |
0,590 |
0,608 |
0,625 |
0,642 |
0,659 |
0,676 |
0,693 |
|
0,379 |
0,396 |
0,414 |
0,432 |
0,449 |
0,467 |
0,484 |
0,502 |
0,519 |
|
1,431 |
1,463 |
1,495 |
1,526 |
1,558 |
1,590 |
1,622 |
1,654 |
1,685 |
t, c |
5,4 |
5,5 |
5,6 |
5,7 |
5,8 |
5,9 |
6 |
6,1 |
6,2 |
|
0,864 |
0,878 |
0,893 |
0,907 |
0,922 |
0,937 |
0,952 |
0,967 |
0,982 |
|
0,709 |
0,725 |
0,742 |
0,758 |
0,774 |
0,790 |
0,805 |
0,821 |
0,837 |
|
0,537 |
0,554 |
0,571 |
0,588 |
0,605 |
0,622 |
0,639 |
0,655 |
0,672 |
|
1,717 |
1,749 |
1,781 |
1,813 |
1,844 |
1,876 |
1,908 |
1,940 |
1,972 |
t, c |
6,3 |
6,4 |
6,5 |
6,6 |
6,7 |
6,8 |
6,9 |
7 |
7,1 |
|
0,997 |
1,013 |
1,025 |
1,034 |
1,041 |
1,045 |
1,048 |
1,049 |
1,049 |
|
0,688 |
0,705 |
0,721 |
0,737 |
0,753 |
0,769 |
0,785 |
0,801 |
0,816 |
|
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
|
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
t, c |
7,2 |
7,3 |
7,4 |
7,5 |
7,6 |
7,7 |
7,8 |
7,9 |
8 |
|
1,047 |
1,045 |
1,041 |
1,037 |
1,033 |
1,028 |
1,023 |
1,017 |
1,012 |
|
0,978 |
0,989 |
0,999 |
1,008 |
1,016 |
1,024 |
1,030 |
1,035 |
1,040 |
|
0,831 |
0,846 |
0,860 |
0,874 |
0,887 |
0,900 |
0,913 |
0,924 |
0,935 |
|
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
t, c |
8,1 |
8,2 |
8,3 |
8,4 |
8,5 |
8,6 |
8,7 |
8,8 |
8,9 |
|
1,007 |
1,002 |
0,997 |
0,992 |
0,988 |
0,984 |
0,980 |
0,977 |
0,974 |
|
1,044 |
1,047 |
1,049 |
1,051 |
1,052 |
1,052 |
1,052 |
1,051 |
1,050 |
|
0,946 |
0,956 |
0,965 |
0,973 |
0,981 |
0,988 |
0,995 |
1,000 |
1,005 |
|
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
t, c |
9 |
9,1 |
9,2 |
9,3 |
9,4 |
9,5 |
9,6 |
9,7 |
9,8 |
|
0,972 |
0,970 |
0,968 |
0,967 |
0,966 |
0,966 |
0,965 |
0,965 |
0,966 |
|
1,049 |
1,047 |
1,044 |
1,042 |
1,039 |
1,037 |
1,034 |
1,031 |
1,028 |
|
1,010 |
1,014 |
1,017 |
1,020 |
1,022 |
1,024 |
1,025 |
1,026 |
1,026 |
|
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
2,000 |
t, c |
9,9 |
10 |
- |
- |
- |
- |
- |
- |
- |
|
0,966 |
0,967 |
- |
- |
- |
- |
- |
- |
- |
|
1,025 |
1,022 |
- |
- |
- |
- |
- |
- |
- |
|
1,026 |
1,026 |
- |
- |
- |
- |
- |
- |
- |
|
2,000 |
2,000 |
- |
- |
- |
- |
- |
- |
- |
Графики реакции цепи при аналитическом методе расчета (сплошная линия) и при численном методе расчета (штриховая линия) представлены на рисунке 17.
Рисунок 17 – Реакция цепи при аналитическом и численном методах решения