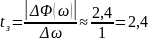МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ТОЭ
отчет
о курсовой работе
по дисциплине «Теоретические основы электротехники»
Тема: «Исследование искажений сигналов на выходе фильтра нижних частот»
Студент гр. 0421 |
|
Токарев А.А. |
Преподаватель |
|
Яшкардин Р.В. |
Санкт-Петербург
2023
СОДЕРЖАНИЕ ВВЕДЕНИЕ 3 1 Задание к курсовой работе 4 2 Нормирование параметров и переменных цепи 5
ВВЕДЕНИЕ
Целью курсовой работы является практическое освоение и сравнение различных методов расчета цепей, прогноза ожидаемых реакций и оценки полученных результатов.
В процессе курсовой работы ставятся следующие задачи:
определение передаточной функции цепи, её частотных и временных характеристик;
исследование реакции цепи при воздействии одиночного импульса;
исследование установившейся реакции цепи при воздействии периодической последовательности импульсов;
Каждый студент получает индивидуальное задание. Курсовая работа представляет собой расчетно-пояснительную записку, содержащую расчетный и графический материал, а также выводы и пояснения.
1 Задание к курсовой работе
Выполняется курсовая работа под вариантом №2. На вход электрической цепи с момента времени t = 0 подается импульс тока i1. Реакцией цепи является ток i2 = iR2. График импульса представлен на рисунке 1.
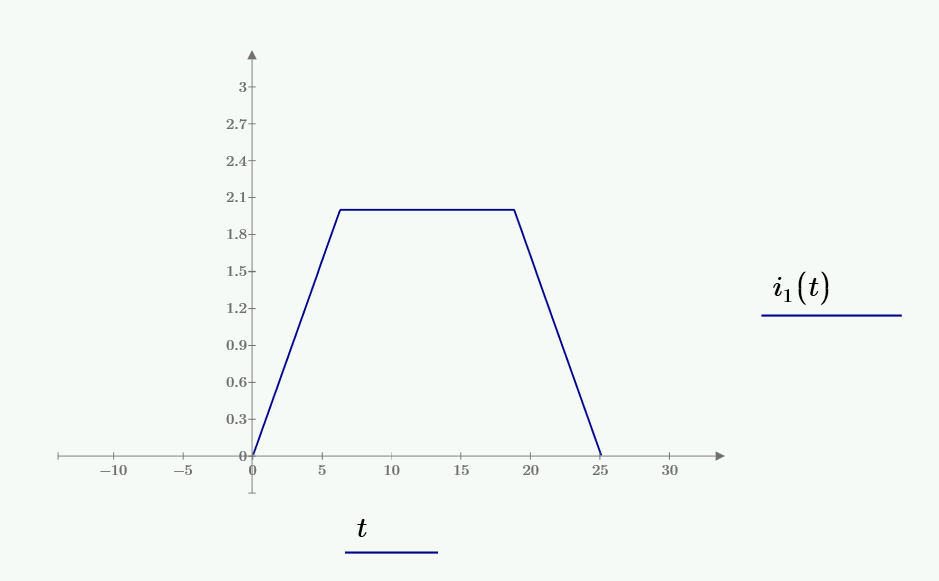
Рисунок 1 – График входного воздействия i1(t)
Схема: 131 – i1, 213 – R2, 313 – C1, 412 – L1, 523 – C2, 623 – R2. Графически схема представлена на рисунке 2.
Рисунок 2 – Исходная схема
Параметры элементов схемы и входного сигнала представлены в таблице 1.
Таблица 1 – Исходные данные
R1 = R2 |
L1 |
C1 |
C2 |
Im |
tи |
T |
0,5 кОм |
1 мГн |
2000 пФ |
2000 пФ |
2 А |
25,12 мкс |
25,12 мкс |
2 Нормирование параметров и переменных цепи
Выберем в качестве базисных параметров Rб = R1 = R2 = 500 Ом, ωб = 106 c-1. Рассчитаем нормированные параметры цепи:
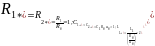
Для упрощения дальнейших записей опустим знак нормировки «*».
3 Определение передаточной функции цепи
Передаточная функция цепи по току определяется следующим соотношением:
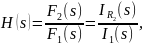
где s – оператор Лапласа. Преобразуем схему замещения в операторную область, вычислим сопротивления:
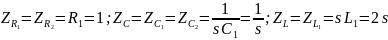
Операторная схема замещения при нулевых начальных условиях представлена на рисунке 3:
Рисунок
3 – Операторная схема замещения при
нулевых начальных условиях
Для нахождения передаточной функции
цепи по току воспользуемся методом
пропорциональных величин. Пусть
.
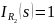Тогда:
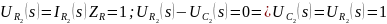
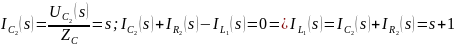
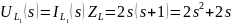
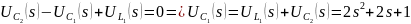
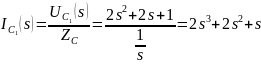
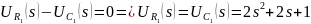
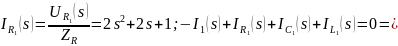
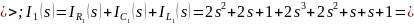
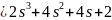
Таким образом, передаточная функция цепи по току будет равна:
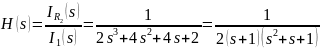
Проконтролируем функцию H(s). Для этого найдем пределы отношений для H(s) при s→0 и при s→∞.
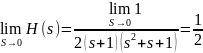
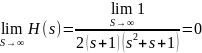
Итак, H(0) = 0,5, H(∞) = 0. Сравним эти значения со значениями полученными по схемам замещения цепи при s→0 и при s→∞. Схемы замещения цепи представлены на рисунках 4 и 5.
Рисунок 4 – Операторная схема замещения цепи при s→0
Найдем передаточную функцию цепи по току при s→0. Так как схема представляет собой делитель тока и оба сопротивления равны между собой, то ток в элементе R2 будет равен половине от тока источника:
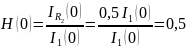
Найдем передаточную функцию цепи по току при s→∞. Так как вместо катушки L1 в схеме будет разрыв, то ток в элементе R2 течь не будет, следовательно:
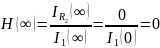
Рисунок 5 – Операторная схема замещения цепи при s→∞
Как можно видеть, результаты расчетов через пределы совпадают с результатами расчетов через схемы замещения. Это говорит о том, что передаточная функция рассчитана правильно.
Найдем нули и полюсы передаточной функции. Так как в числителе передаточной функции нет оператора Лапласа s, то у данной передаточной функции нет нулей. Чтобы найти полюса, необходимо найти корни характеристического полинома цепи (знаменателя передаточной функции):
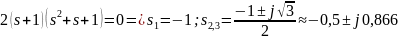
Расположение полюсов передаточной функции представлено на рисунке 6.
Рисунок 6 – Расположение полюсов передаточной функции цепи на комплексной плоскости
Оценим практическую длительность переходных процессов в цепи:
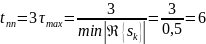
4 Расчет частотных характеристик цепи
Найдем обобщенную частотную характеристику цепи:
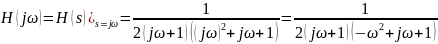
Упростим обобщенную характеристику цепи:
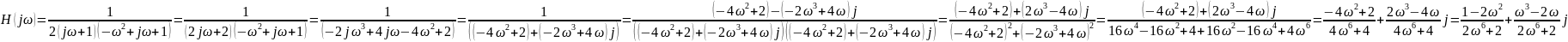
Таким образом, мы получили вещественную
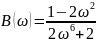и мнимую
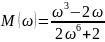частотные характеристики. График
АФХ представлен на рисунке 7.
Рисунок 7 – АФХ цепи
Найдем АЧХ:
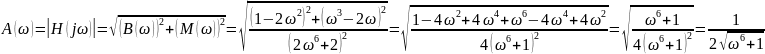
Построим график АЧХ. График АЧХ представлен на рисунке 8.
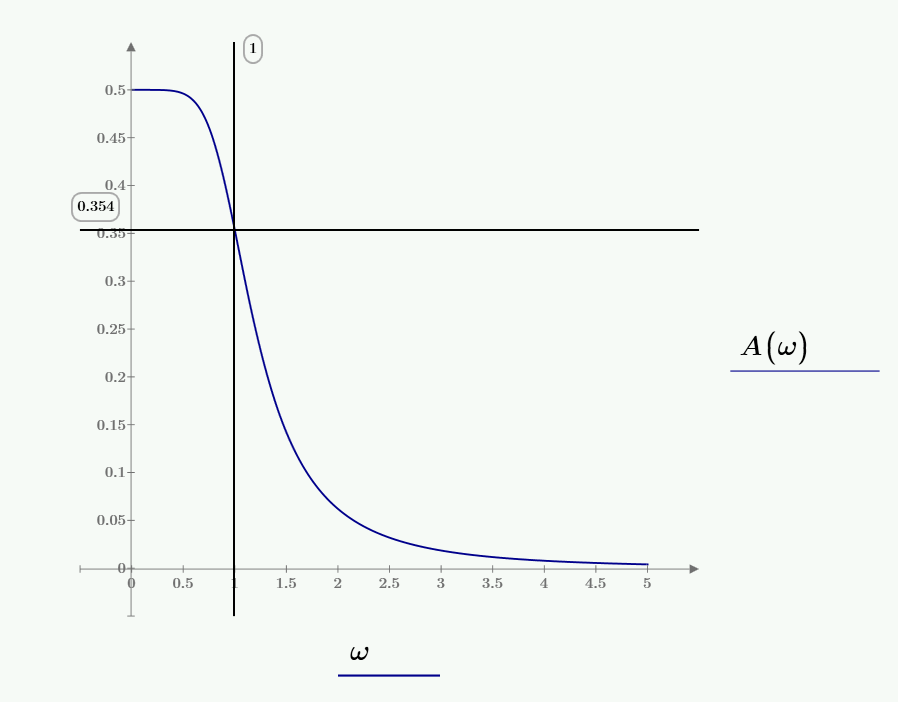
Рисунок 8 – АЧХ цепи
Определим полосу пропускания по графику АЧХ на уровне 0,707Аmax(ω)≈0,354. Частота среза ωср ≈ 1, полоса пропускания Δωп ϵ [0;1], что соответствует фильтру нижних частот. Значение АЧХ на нулевой частоте, определяющее соотношение площадей под графиками входного и выходного сигналов, А(0) = 0,5. Так как А(∞) = 0, то график выходного сигнала должен быть непрерывным (без скачков).
Найдем ФЧХ:
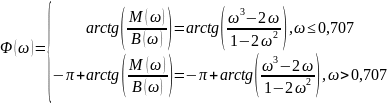
Построим график ФЧХ. График ФЧХ цепи представлен на рисунке 9.
Рисунок 9 – ФЧХ цепи
Анализ ФЧХ показывает, что в полосе пропускания Δωп ϵ [0;1] она близка к линейной. Следовательно, в случае попадания спектра воздействия в полосу пропускания цепи, искажения формы сигнала не будут существенными.
Оценим время запаздывания по наклону графика ФЧХ в области низких частот:
