4. Исследование систем с реле гистерезисного типа с зоной нечувствительности

Соберем схему системы для случая реле гистерезисного типа с зоной нечувствительности, отсутствия коррекции по скорости и нулевого входного сигнала. Установим параметры звеньев согласно таблице 1. Схема представлена на рисунке 39.

Рисунок 39 – Структурная схема для исследования свободного движения системы

Построим фазовый портрет для малого отклонения x₁₀ = 1. Для этого построим зависимость x₂(t) от x₁(t). Фазовый портрет представлен на рисунке 40.

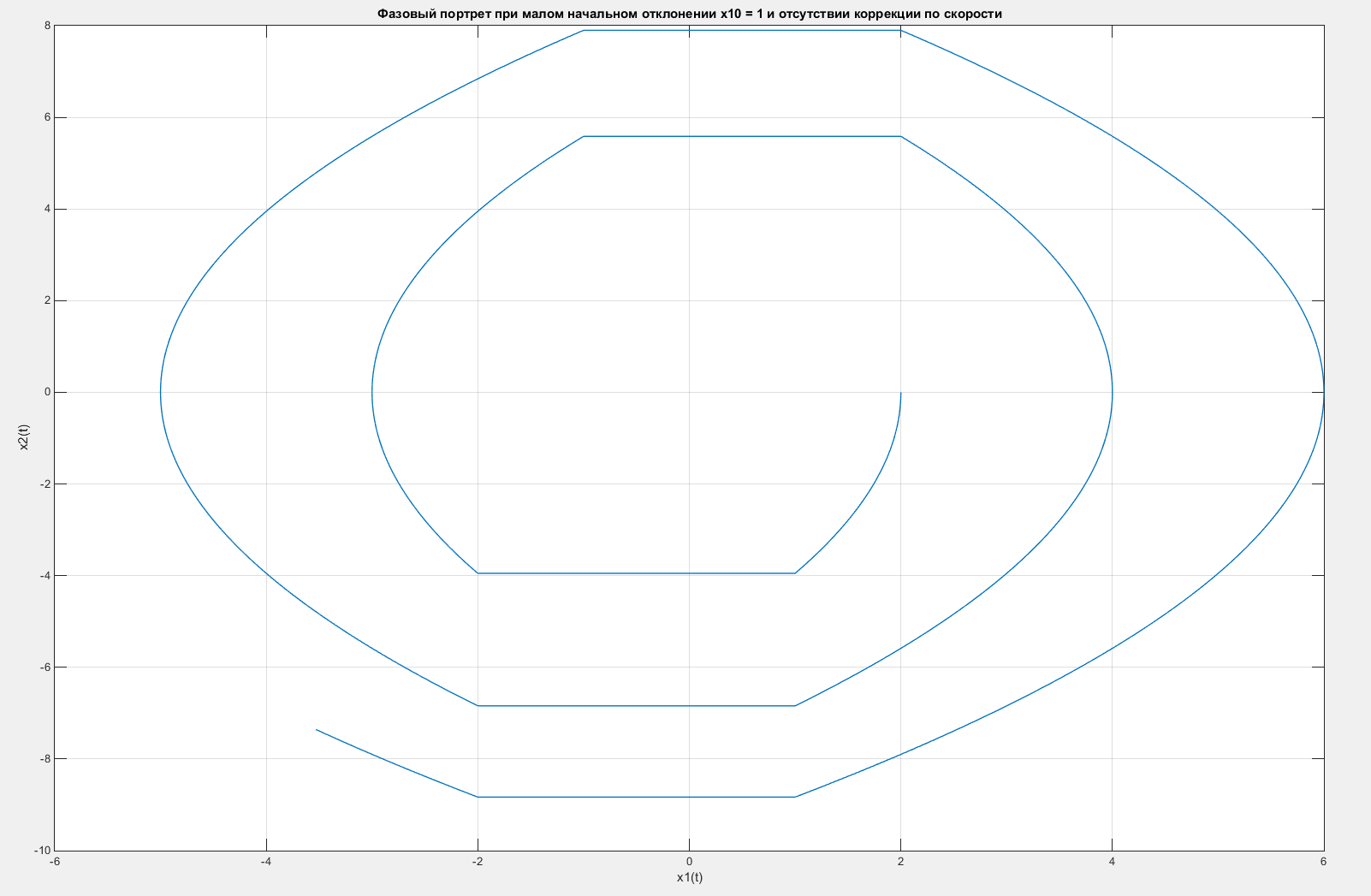
Рисунок 40 – Фазовый портрет системы для случая малого начального отклонения

Графики зависимости x₁(t) и x₂(t) представлены на рисунке 41.

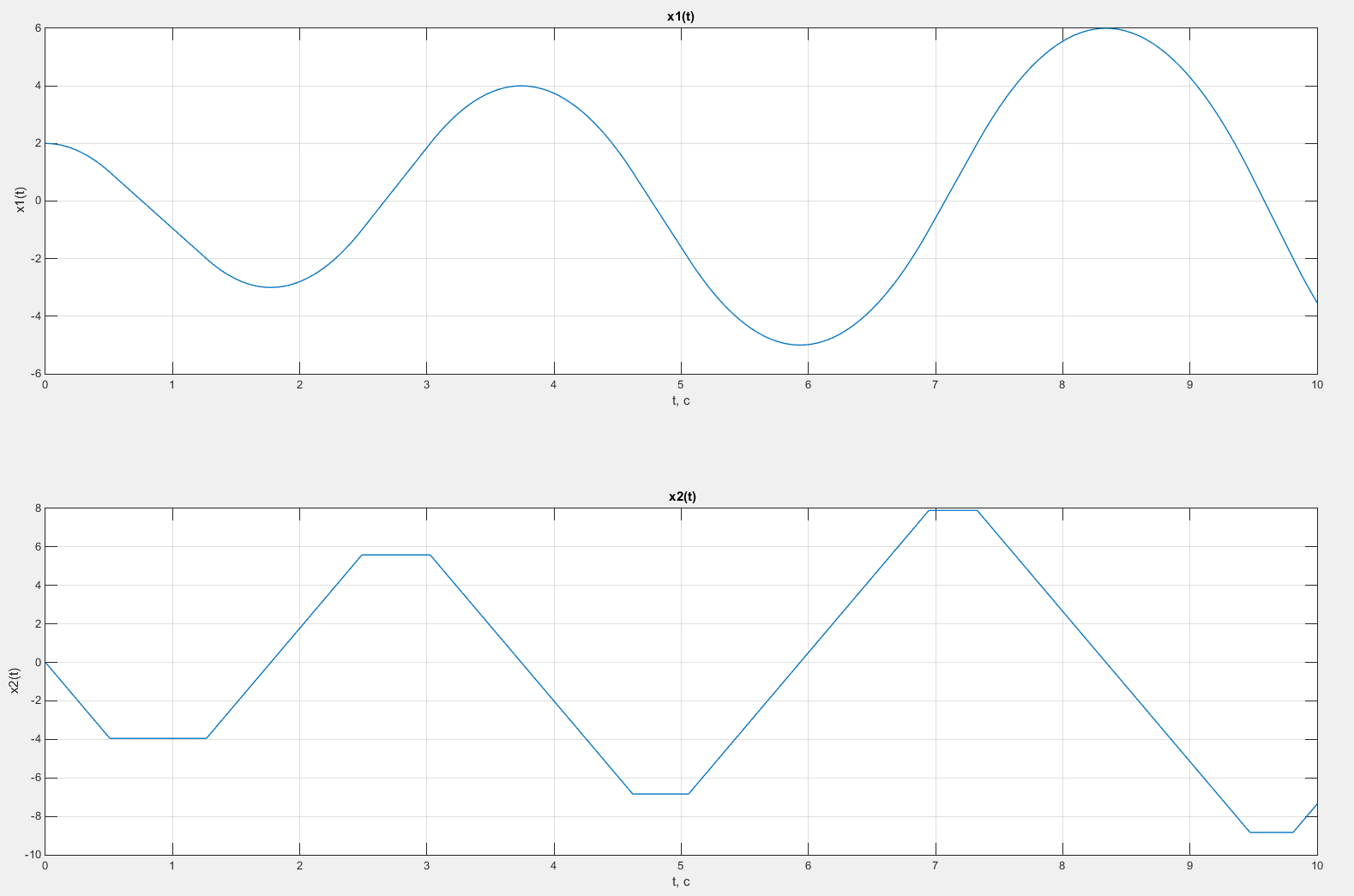
Рисунок 41 - Графики зависимостей x₁(t) и x₂(t) для случая малого начального отклонения

Введем коррекцию по скорости. Схема с коррекцией по скорости представлена на рисунке 42.

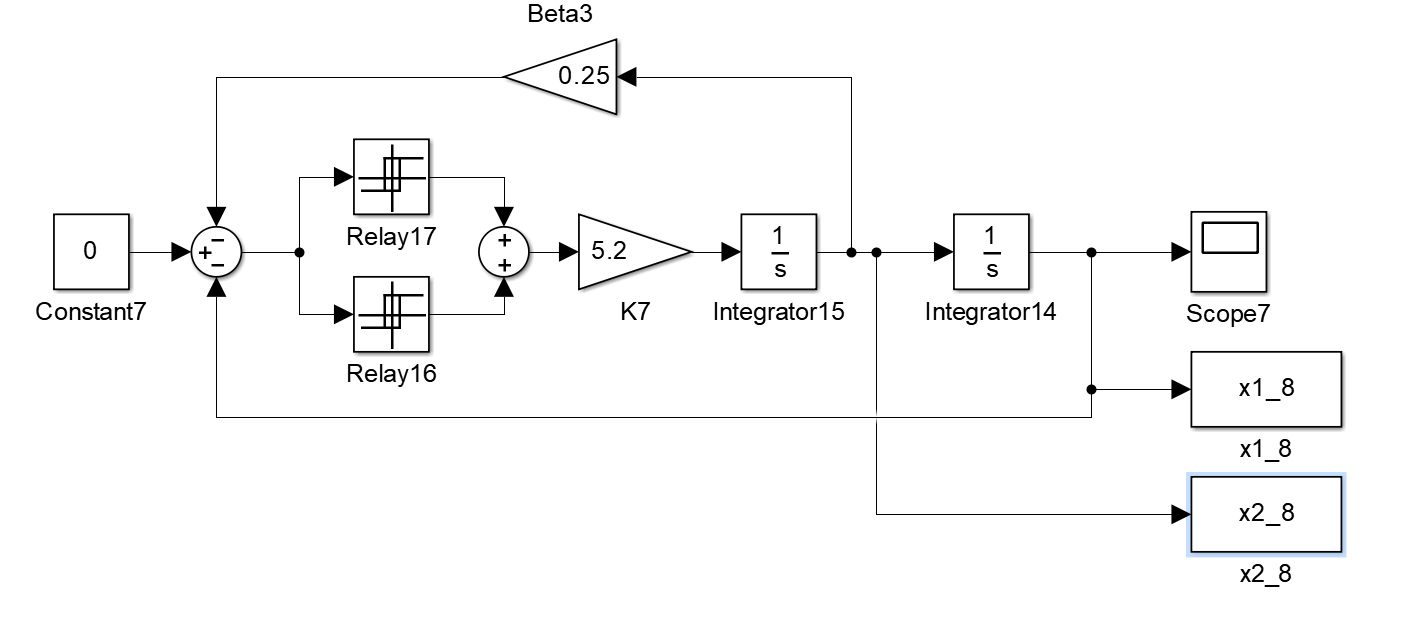
Рисунок 42 – Схема системы с введенной коррекцией по скорости

Зададим коэффициент обратной связи β = 0,25; 0,5; 1 и построим фазовые портреты и графики изменения x₁(t) и x₂(t) для этих значений коэффициента β. Фазовые портреты, а также графики изменения x₁(t) и x₂(t) для системы с различными коэффициентами обратной связи представлены на рисунках 43 –48.

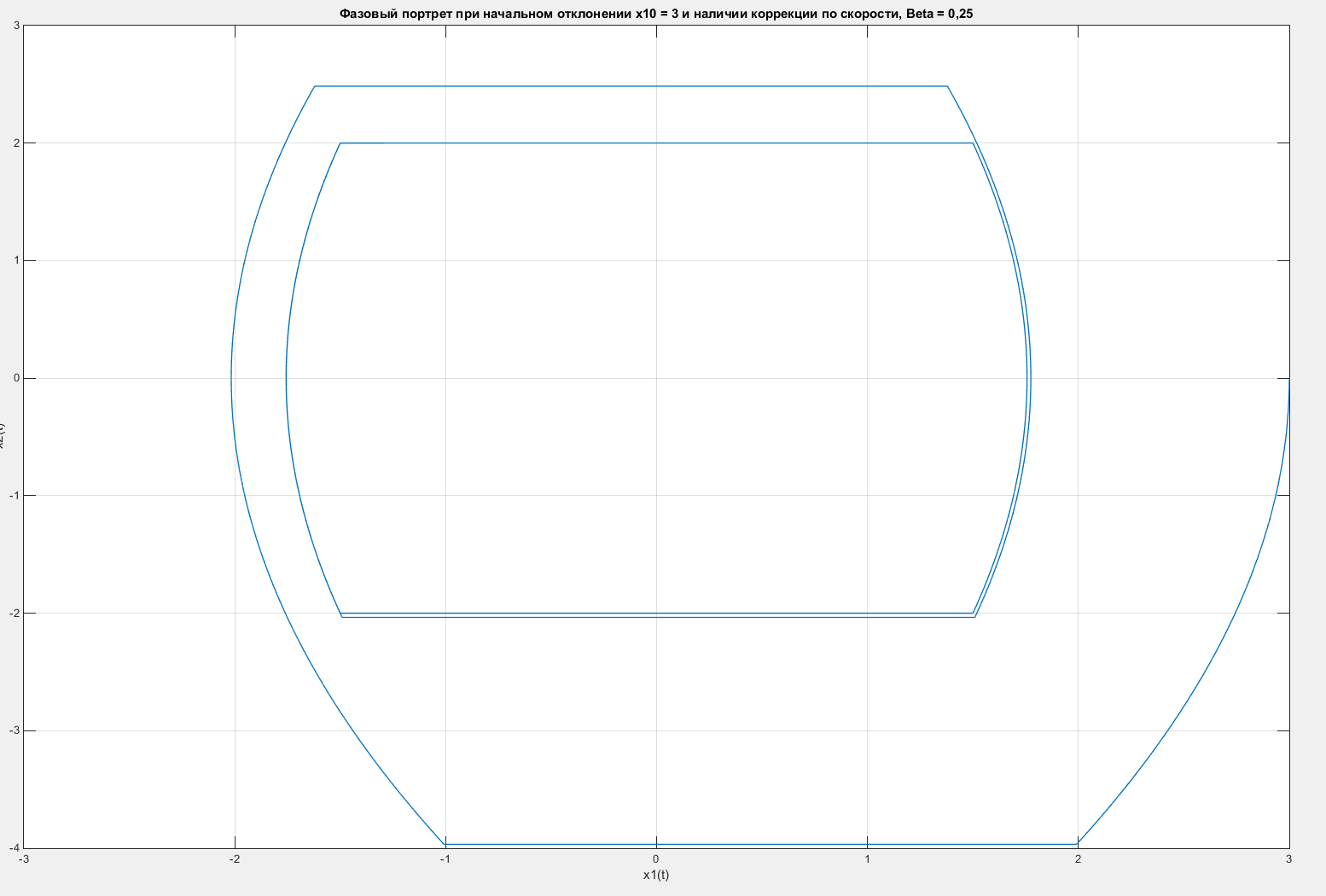
Рисунок 43 – Фазовый портрет системы с введенной коррекцией по скорости с коэффициентом β = 0,25

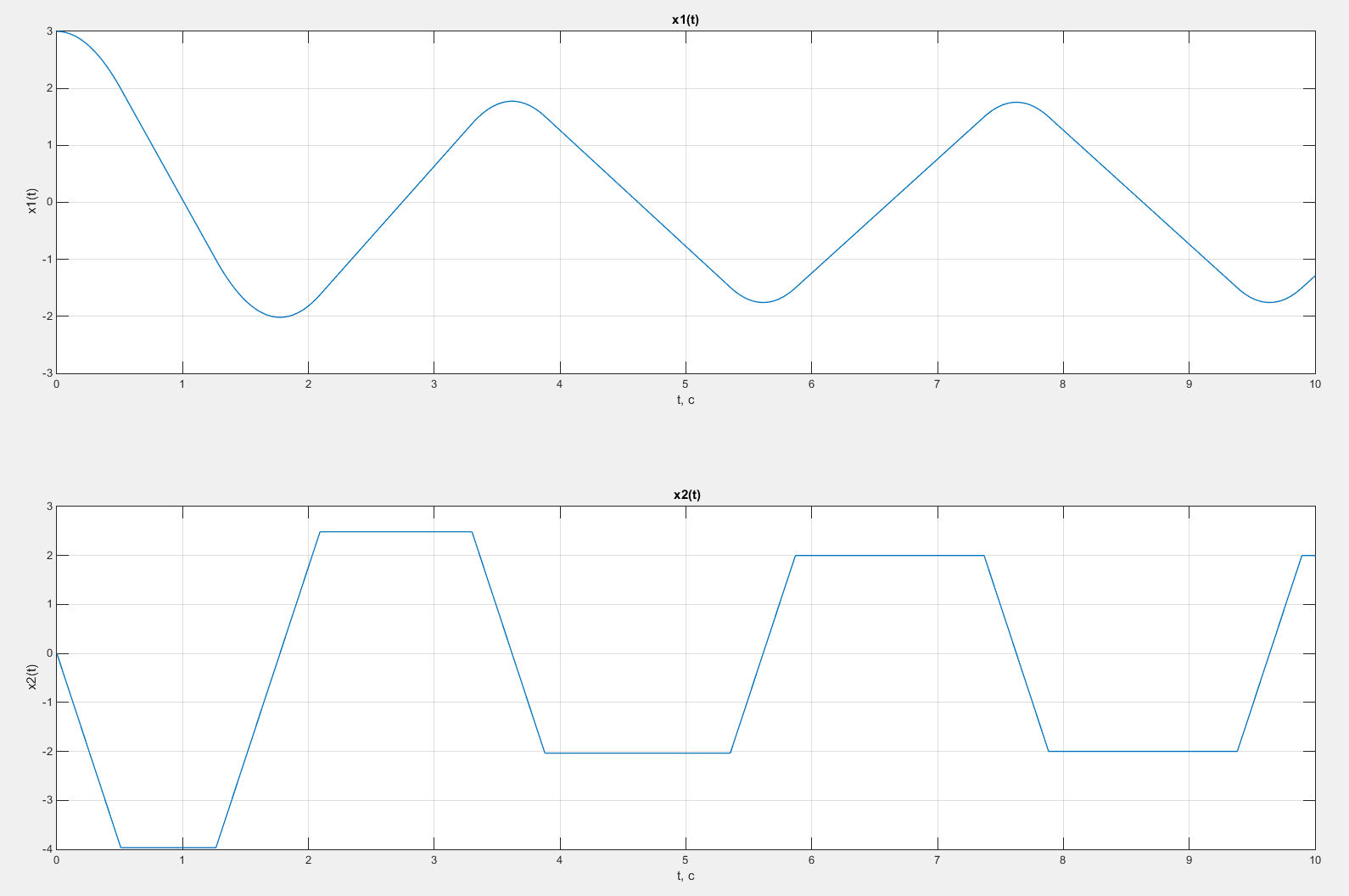
Рисунок 44 – Графики зависимостей x₁(t) и x₂(t) в случае введения коррекции по скорости с коэффициентом β = 0,25

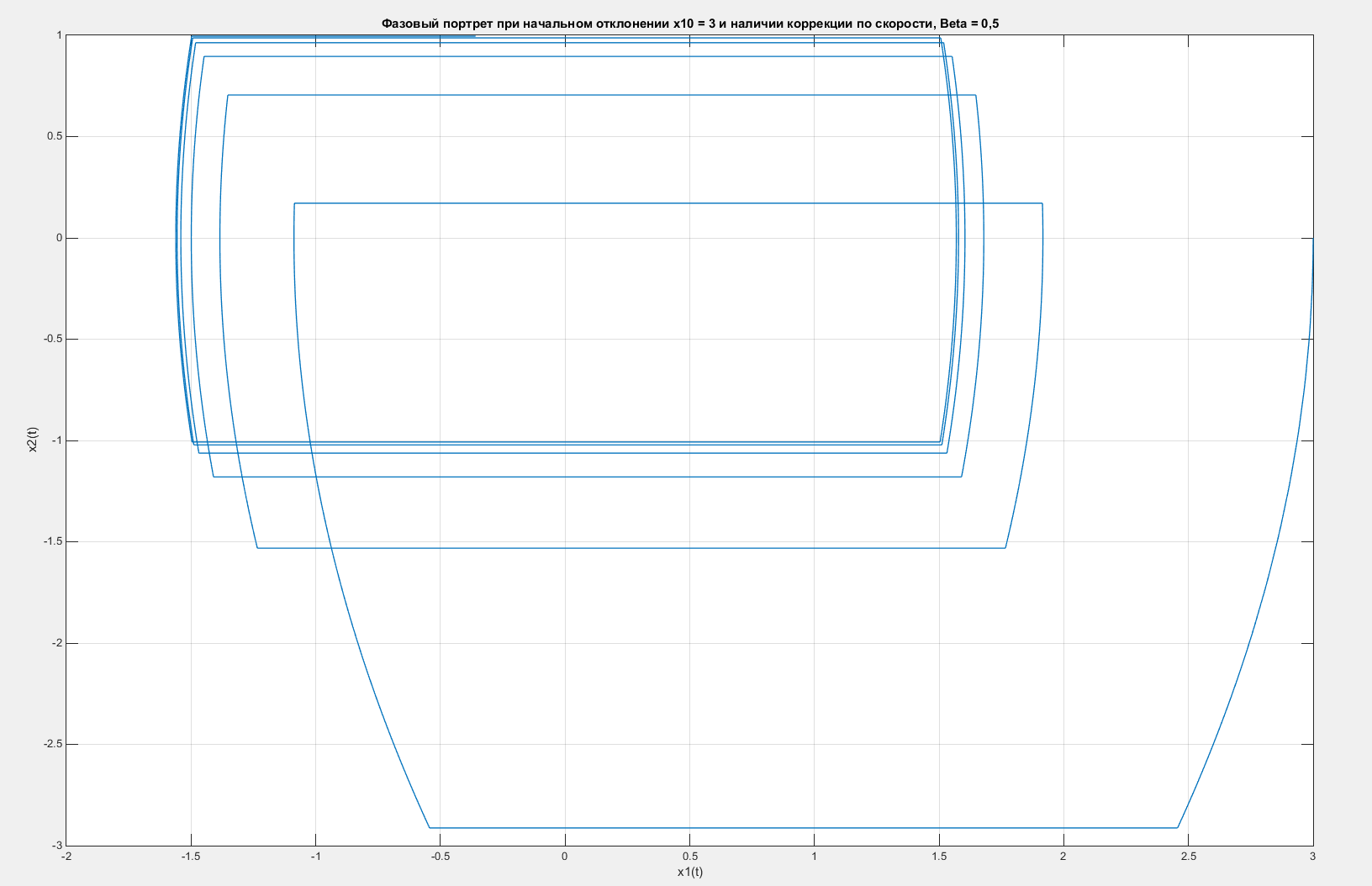
Рисунок 45 – Фазовый портрет системы с введенной коррекцией по скорости с коэффициентом β = 0,5

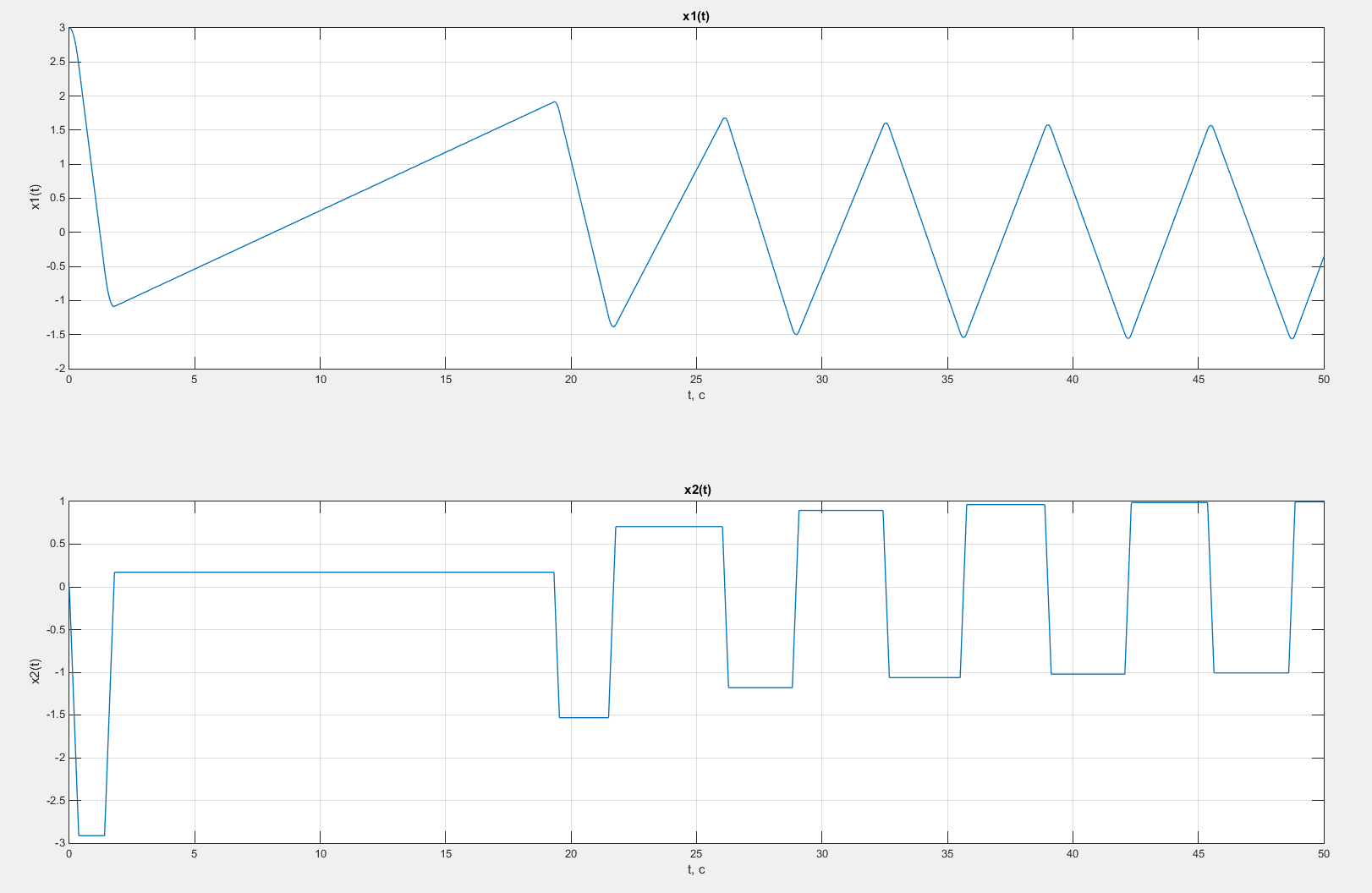
Рисунок 46 – Графики зависимостей x₁(t) и x₂(t) в случае введения коррекции по скорости с коэффициентом β = 0,5

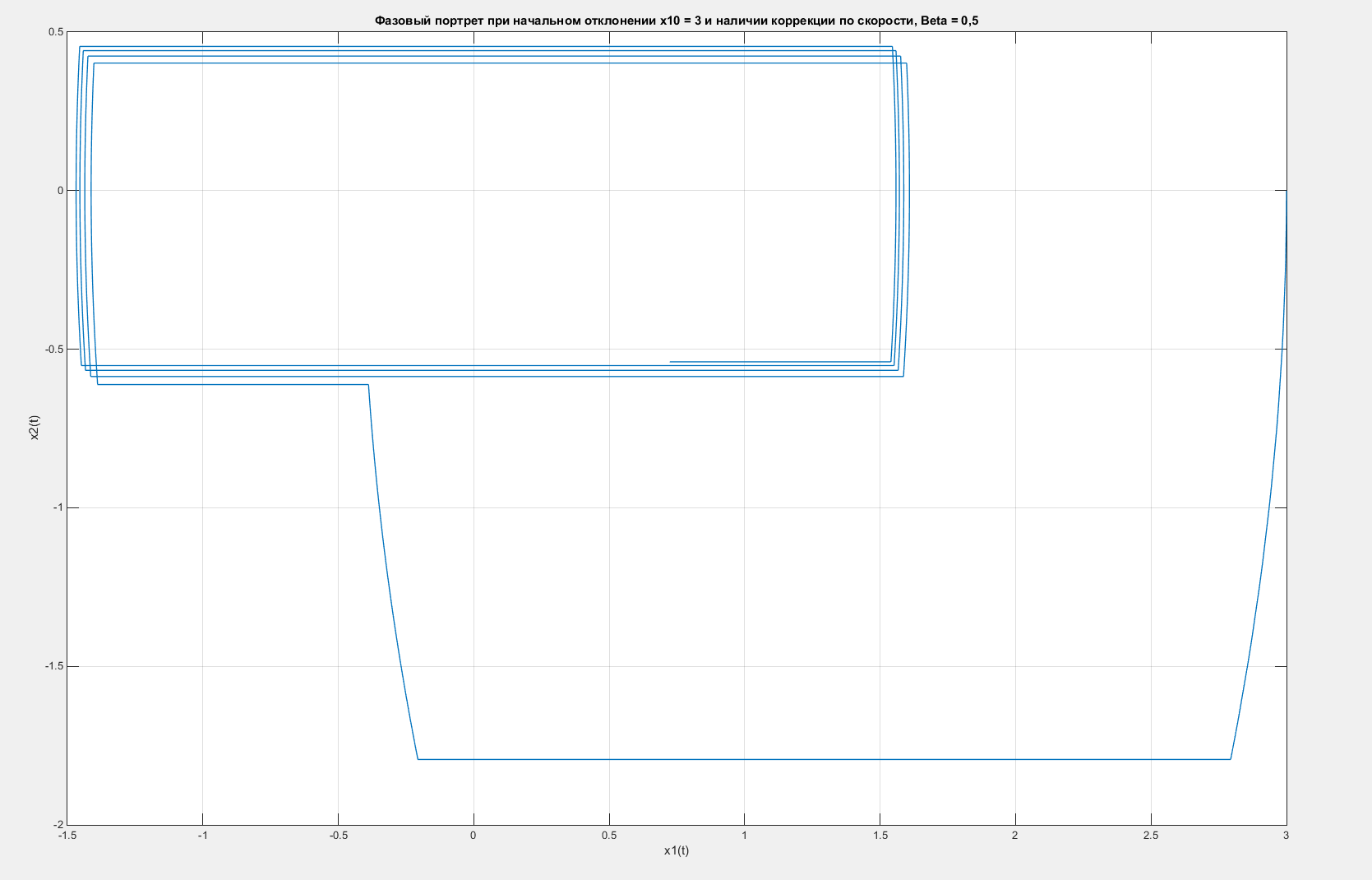
Рисунок 47 – Фазовый портрет системы с введенной коррекцией по скорости с коэффициентом β = 1

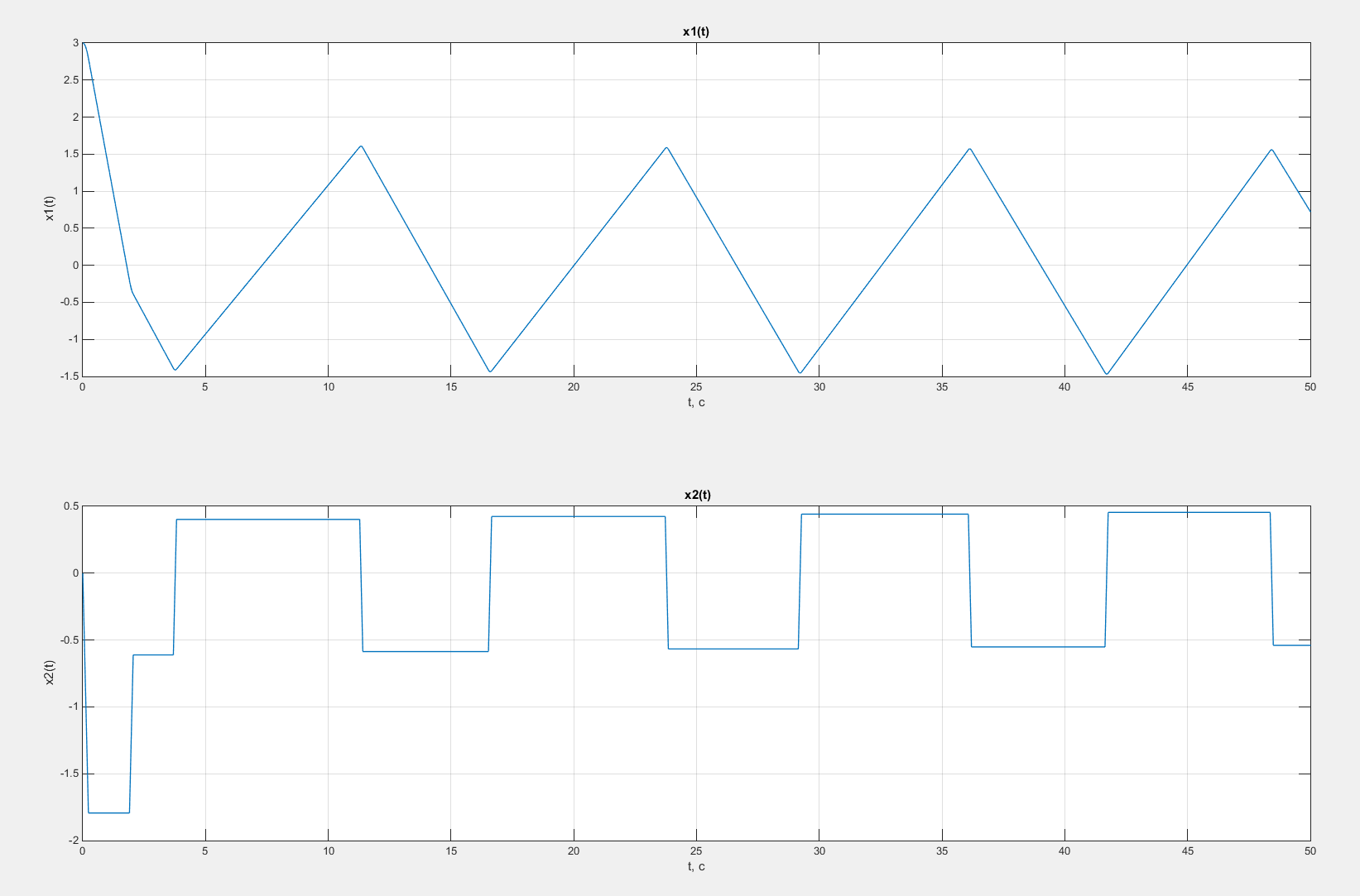
Рисунок 48 – Графики зависимостей x₁(t) и x₂(t) в случае введения коррекции по скорости с коэффициентом β = 1

5. Исследование объекта управления вида

   1. Исследование систем с идеальным двухпозиционным реле

Соберем схему системы для случая идеального двухпозиционного реле, отсутствия коррекции по скорости и нулевого входного сигнала. Установим параметры звеньев согласно таблице 1. Схема представлена на рисунке 49.

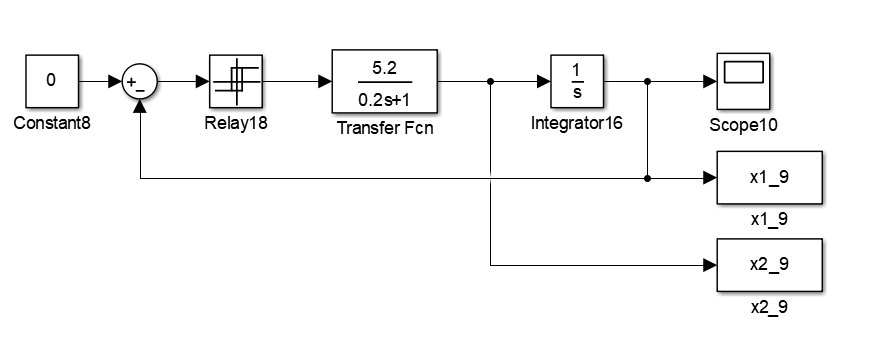
Рисунок 49 – Структурная схема для исследования свободного движения системы

Построим фазовый портрет для случая свободного движения системы. Для этого построим зависимость x₂₀(t) от x₁₀(t). Фазовый портрет представлен на рисунке 50.

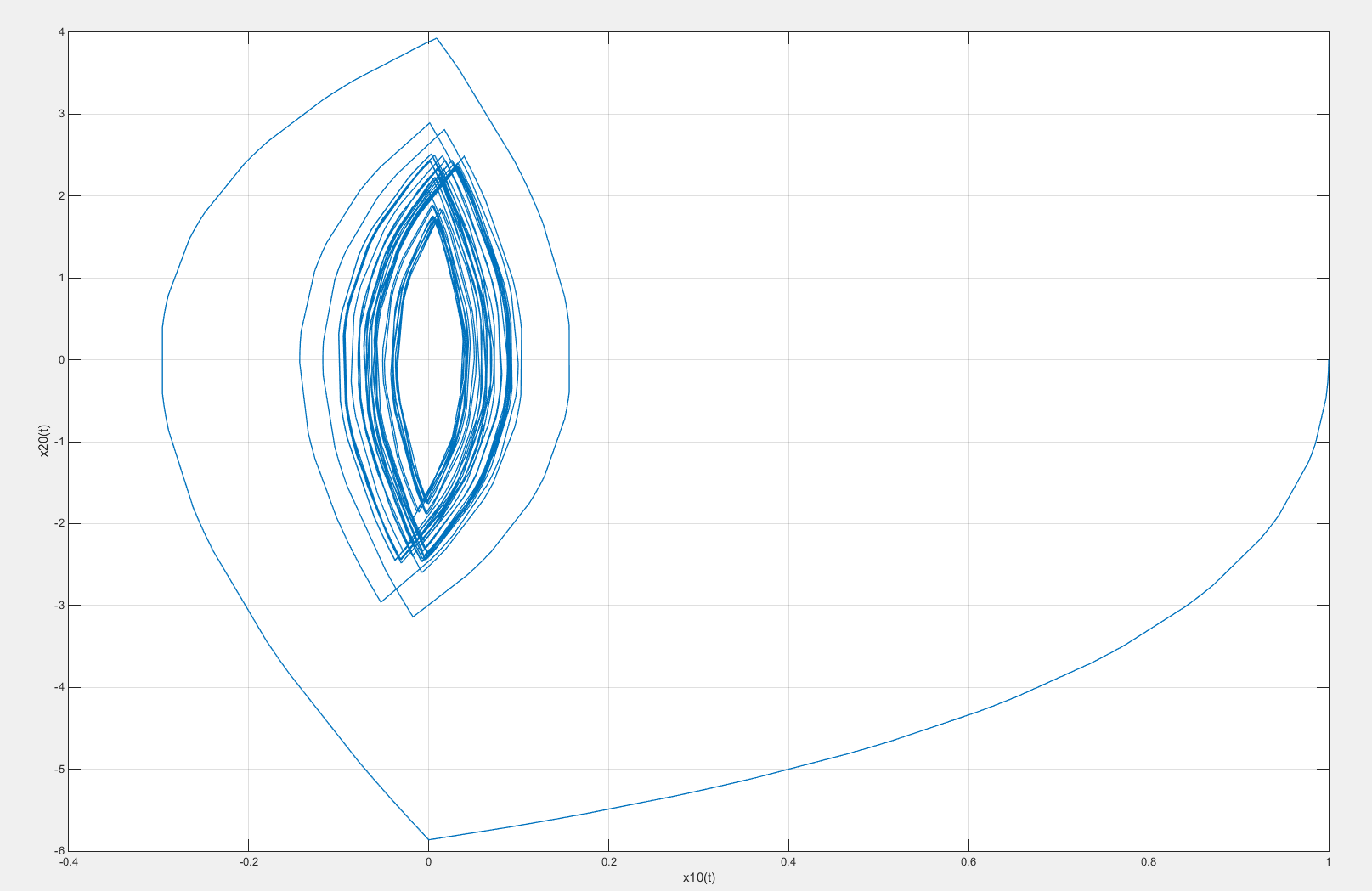
Рисунок 50 – Фазовый портрет свободного движения системы

Графики зависимости x₁(t) и x₂(t) представлены на рисунке 51.

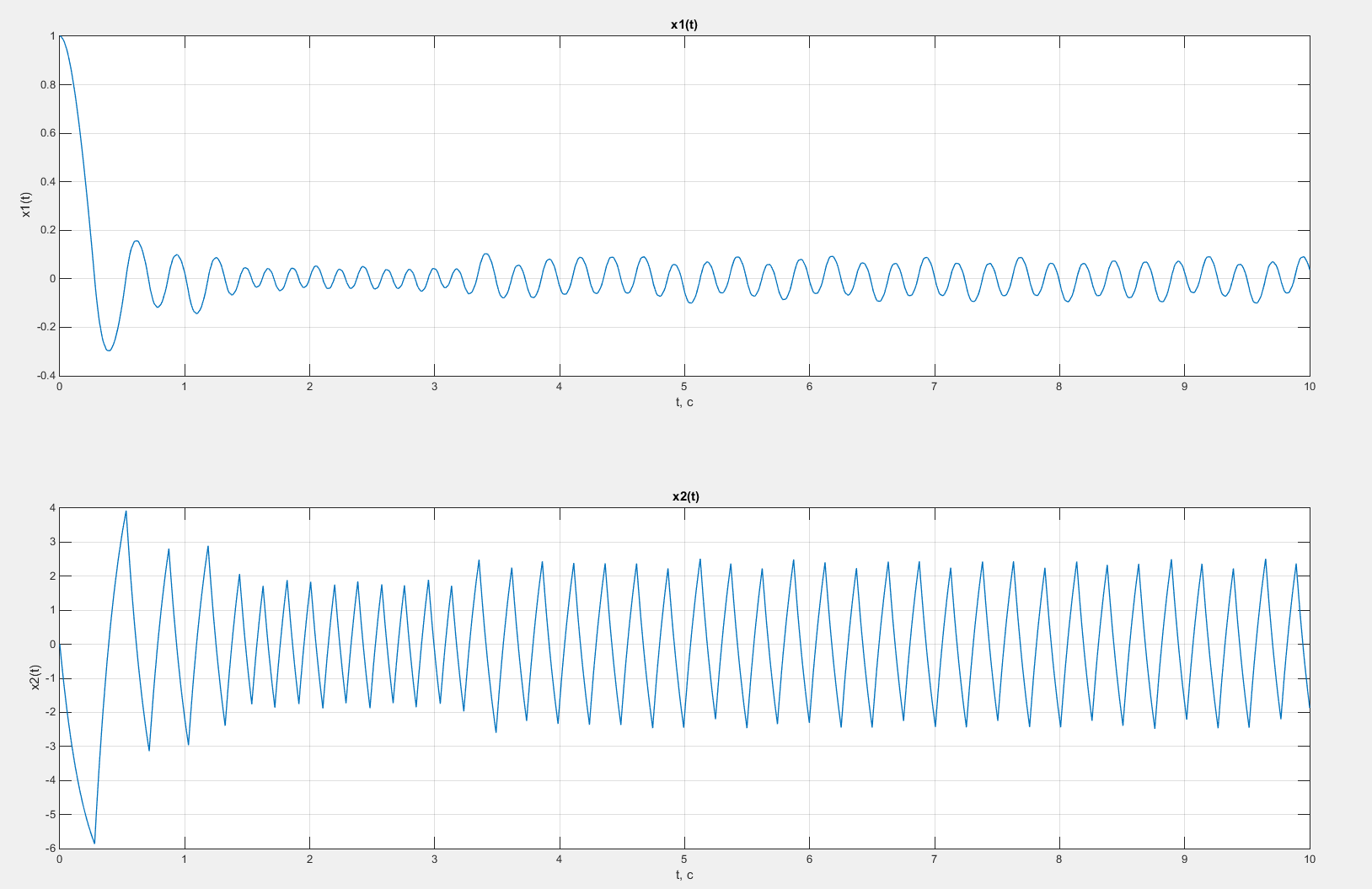
Рисунок 51 – Графики зависимостей x₁(t) и x₂(t) в случае свободного движения системы

Введем коррекцию по скорости. Схема с коррекцией по скорости представлена на рисунке 52.

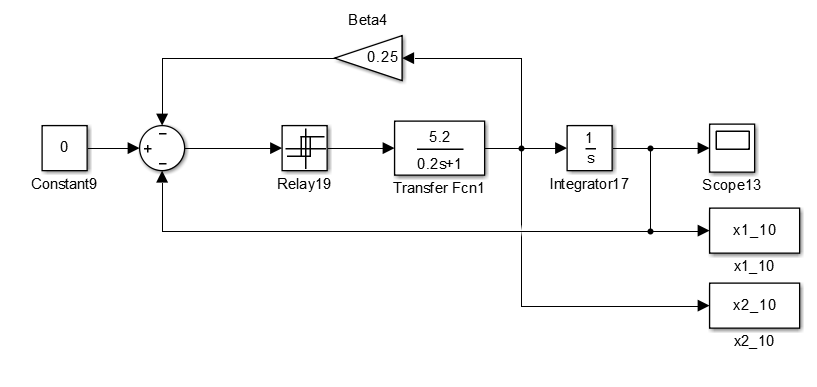
Рисунок 52 – Схема системы с введенной коррекцией по скорости

Зададим коэффициент обратной связи β = 0,25; 0,5; 1 и построим фазовые портреты и графики изменения x₁(t) и x₂(t) для этих значений коэффициента β. Фазовые портреты, а также графики изменения x₁(t) и x₂(t) для системы с различными коэффициентами обратной связи представлены на рисунках 53 –58.

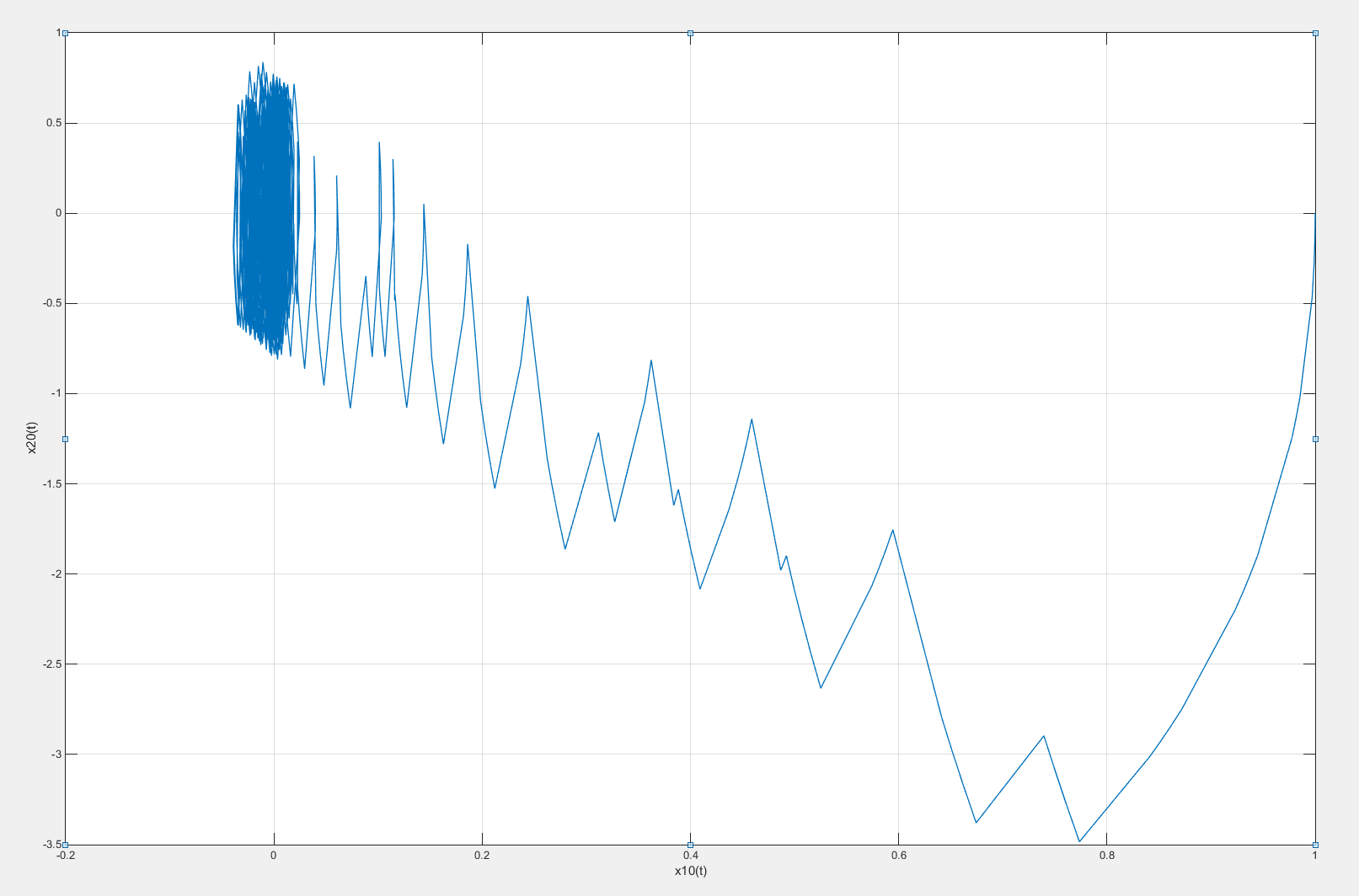
Рисунок 53 – Фазовый портрет системы с введенной коррекцией по скорости с коэффициентом β = 0,25

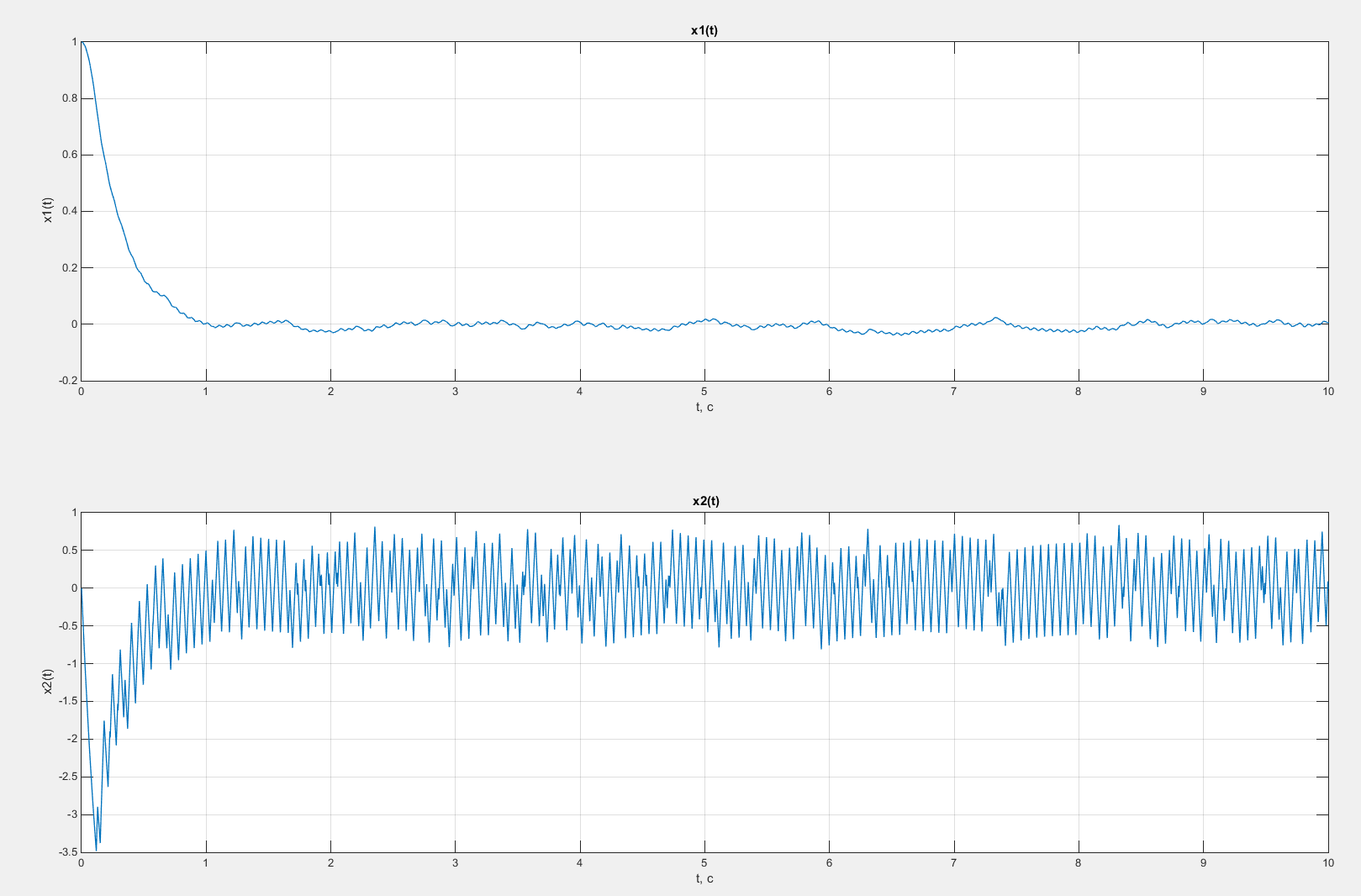
Рисунок 54 – Графики зависимостей x₁(t) и x₂(t) в случае введения коррекции по скорости с коэффициентом β = 0,25

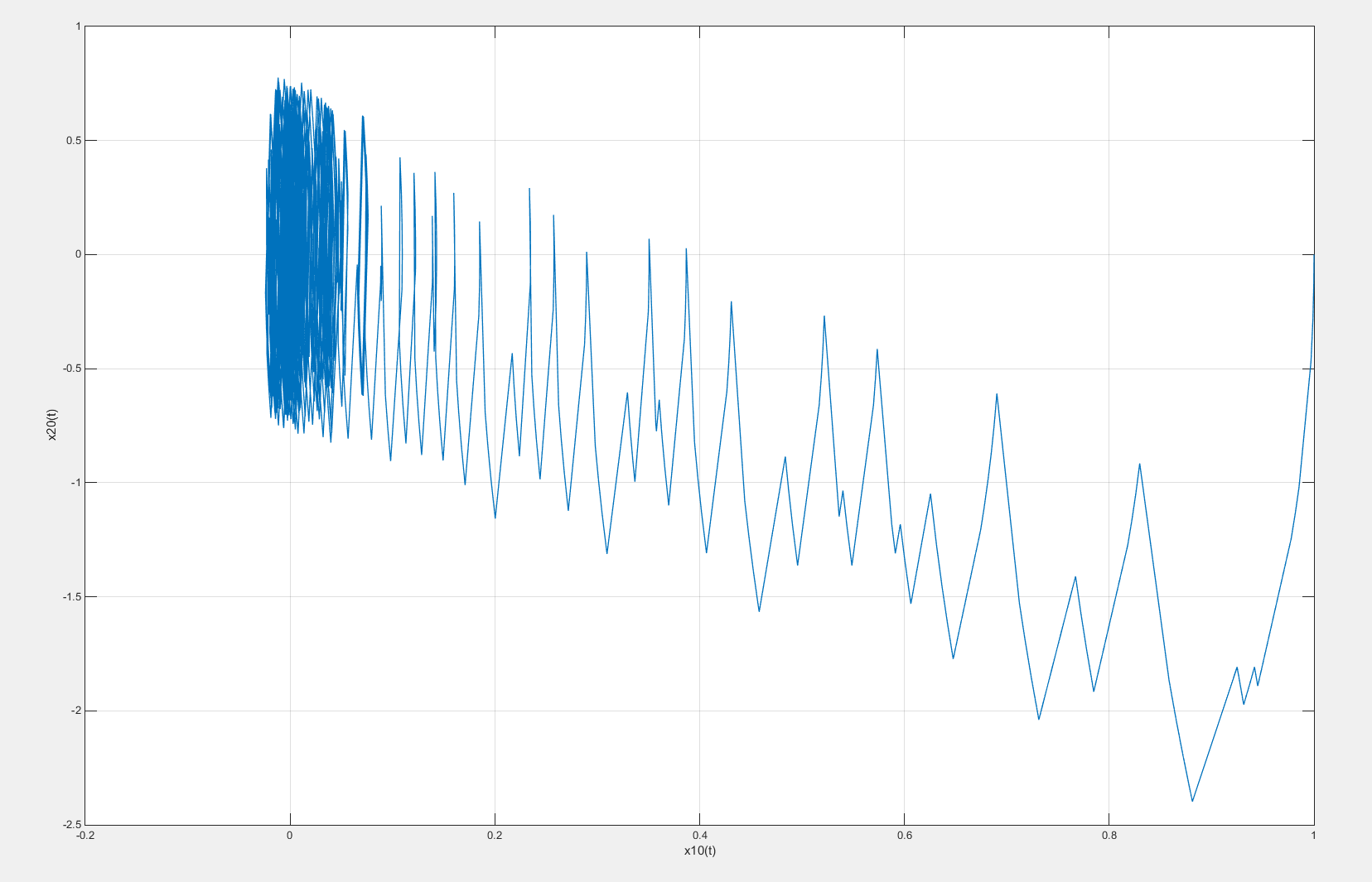
Рисунок 55 – Фазовый портрет системы с введенной коррекцией по скорости с коэффициентом β = 0,5

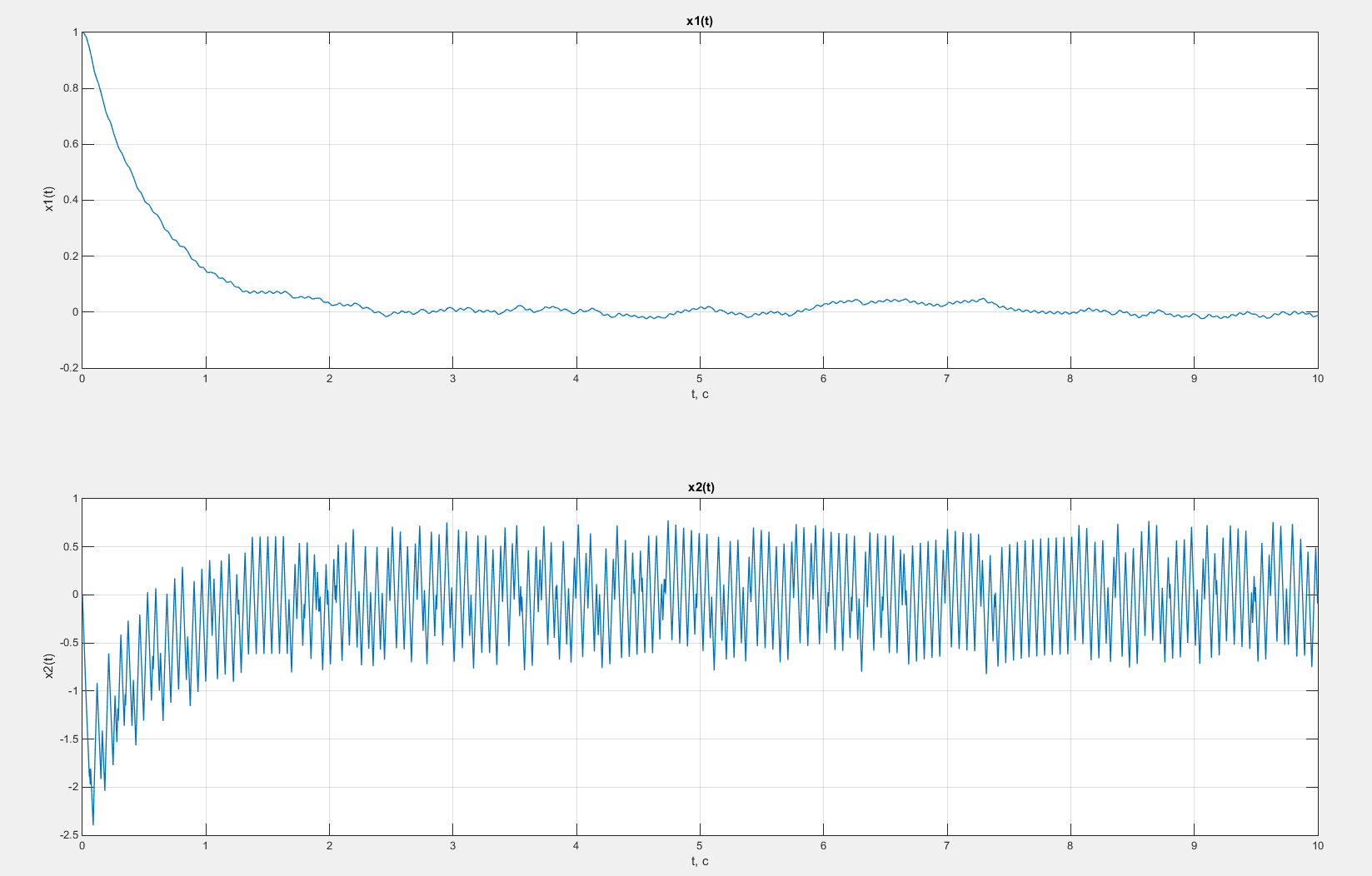
Рисунок 56 – Графики зависимостей x₁(t) и x₂(t) в случае введения коррекции по скорости с коэффициентом β = 0,5

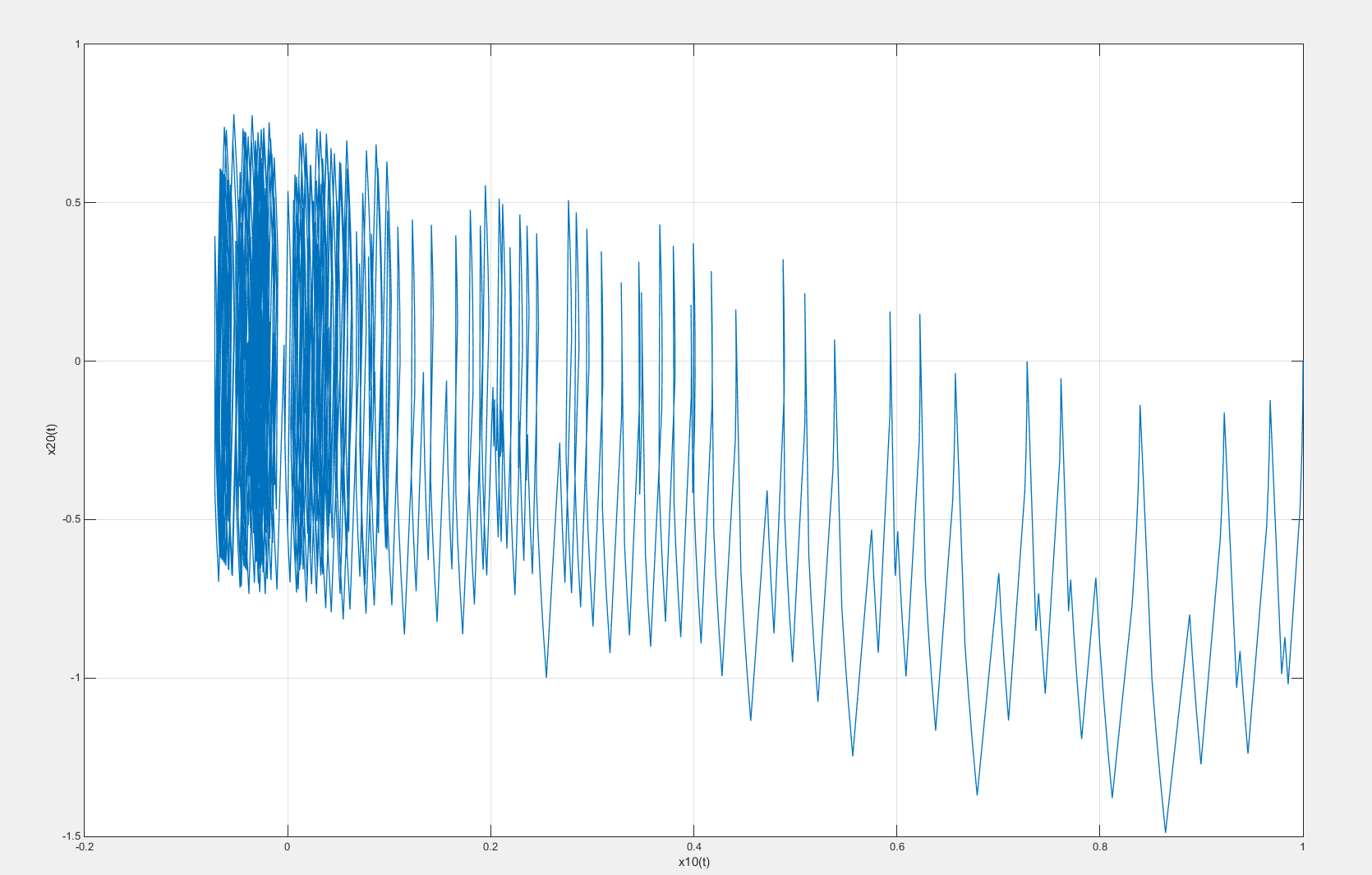
Рисунок 57 – Фазовый портрет системы с введенной коррекцией по скорости с коэффициентом β = 1

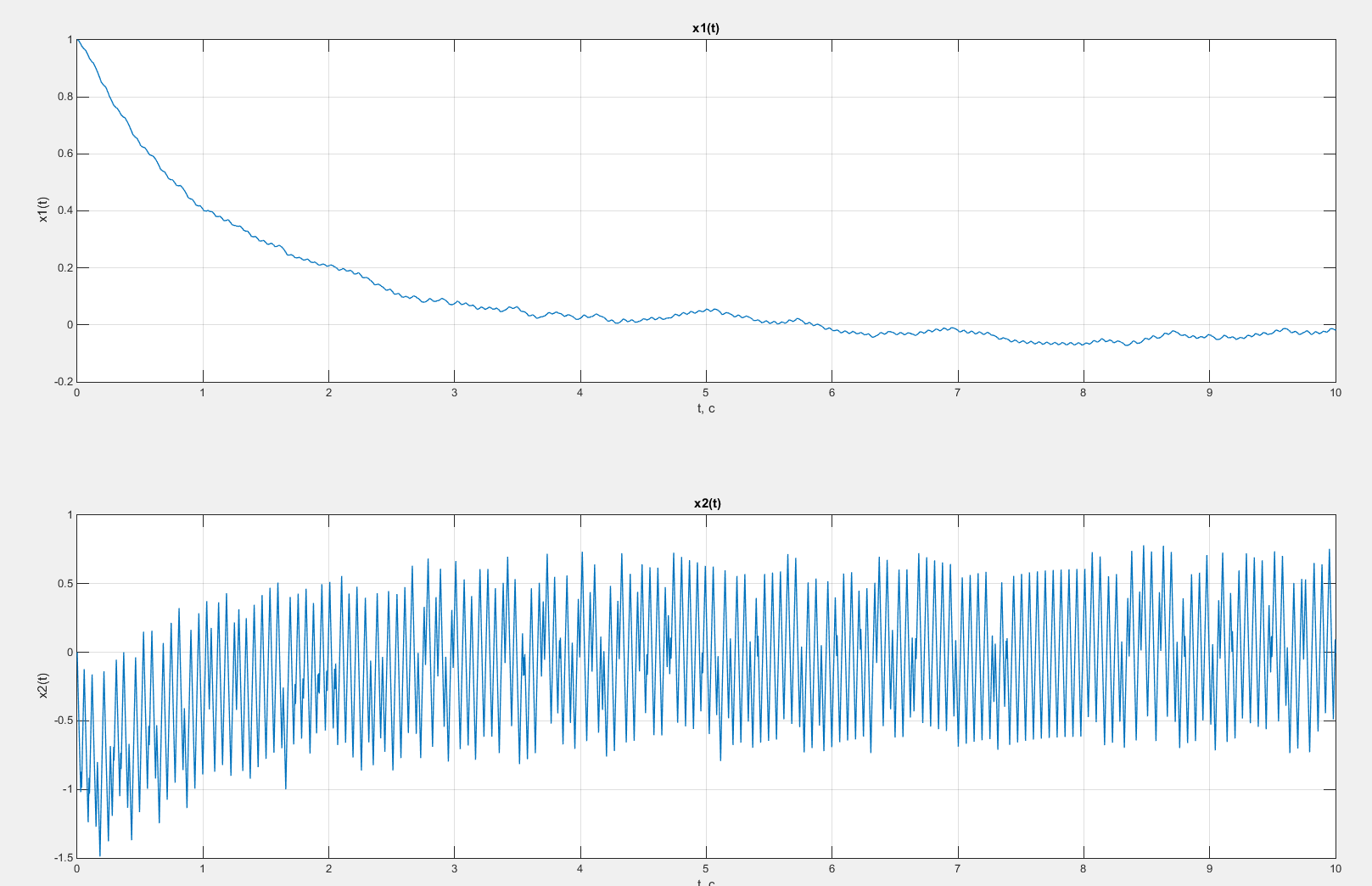
Рисунок 58 – Графики зависимостей x₁(t) и x₂(t) в случае введения коррекции по скорости с коэффициентом β = 1