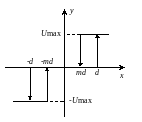
- •Цель работы
- •Исходные данные
- •Исследование типовых нелинейностей
- •Исследование объекта управления вида
- •Исследование систем с идеальным двухпозиционным реле
- •Исследование систем с реле с зоной нечувствительности
- •Исследование систем с реле гистерезисного типа
- •Исследование систем с реле гистерезисного типа с зоной нечувствительности
- •Исследование объекта управления вида
- •Исследование систем с идеальным двухпозиционным реле
- •Исследование систем с реле с зоной нечувствительности
- •Исследование систем с реле гистерезисного типа
- •Исследование систем с реле гистерезисного типа с зоной нечувствительности
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра РАПС
отчет
по лабораторной работе № 4
по дисциплине «Теория автоматического управления»
Тема: «Исследование релейной системы автоматического управления методом фазовой плоскости»
Студент гр. 0421 |
|
Токарев А.А. |
Преподаватель |
|
Благодарный Н.С. |
Санкт-Петербург
2023
Содержание
1. Цель работы 3
2. Исходные данные 3
3. Исследование типовых нелинейностей 3
4. Исследование объекта управления вида 7
4.1. Исследование систем с идеальным двухпозиционным реле 7
4.2. Исследование систем с реле с зоной нечувствительности 12
4.3. Исследование систем с реле гистерезисного типа 17
4.4. Исследование систем с реле гистерезисного типа с зоной нечувствительности 22
5. Исследование объекта управления вида 27
5.1. Исследование систем с идеальным двухпозиционным реле 27
5.2. Исследование систем с реле с зоной нечувствительности 32
5.3. Исследование систем с реле гистерезисного типа 37
5.4. Исследование систем с реле гистерезисного типа с зоной нечувствительности 42
Вывод 47
Цель работы
Изучение базовых нелинейных блоков и их динамических характеристик;
Исследование динамики нелинейных систем второго порядка методом фазовой плоскости.
Исходные данные
Исходные данные для выполнения лабораторной работы представлены в таблице 1.
Таблица 1 – Исходные данные
Вариант |
Вид нелинейности |
m |
Umax |
d |
xm |
K |
T, с |
13 |
|
0,5 |
1,5 |
2 |
3 |
5,2 |
0,2 |
Исследование типовых нелинейностей
Соберем схему для исследования идеального двухпозиционного реле из библиотеки Discontinues. На вход реле подадим сигнал x(t) = 3sin(0.01t) и зафиксируем статические и динамические характеристики элемента. Схема представлена на рисунке 1.
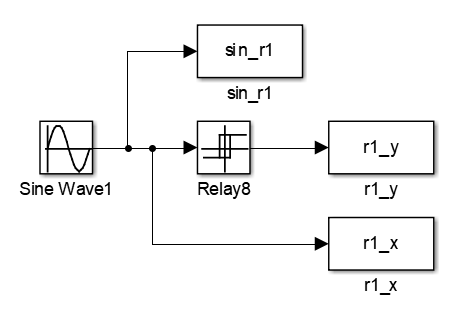
Рисунок 1 – Схема для исследования идеального двухпозиционного реле
Построим статические и динамические характеристики идеального двухпозиционного реле. Характеристики представлены на рисунке 2.
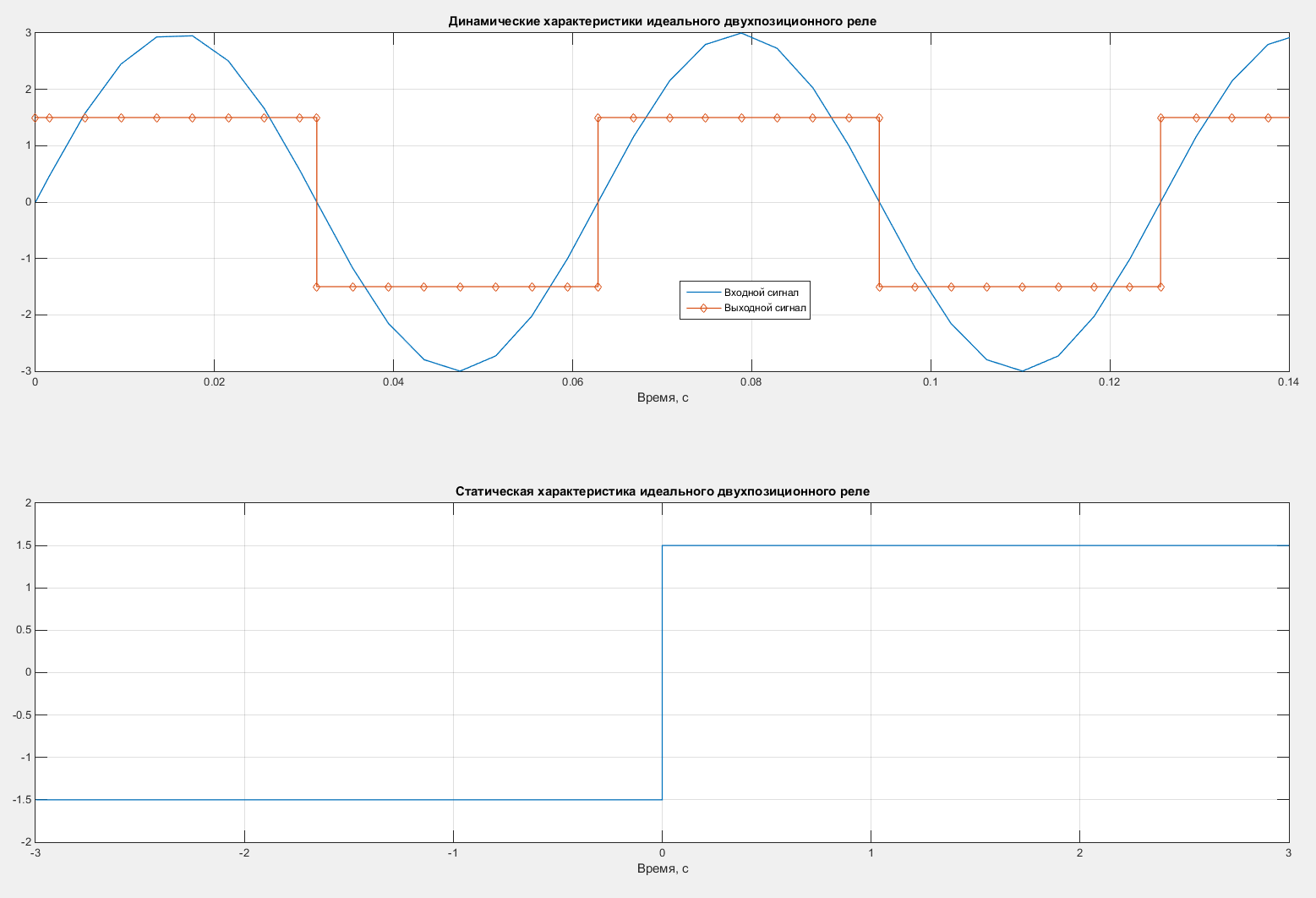
Рисунок 2 – Статические и динамические характеристики идеального двухпозиционного реле
Соберем схему для исследования реле с зоной нечувствительности. На вход реле подадим сигнал x(t) = 3sin(0.01t) и зафиксируем статические и динамические характеристики элемента. Схема представлена на рисунке 3.
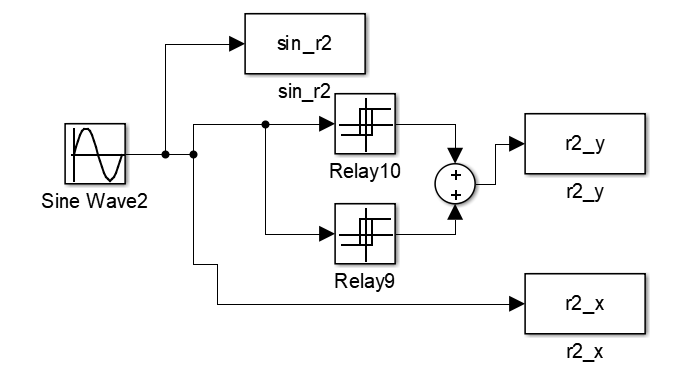
Рисунок 3 – Схема для исследования реле с зоной нечувствительности
Построим статические и динамические характеристики реле c зоной нечувствительности. Характеристики представлены на рисунке 4.
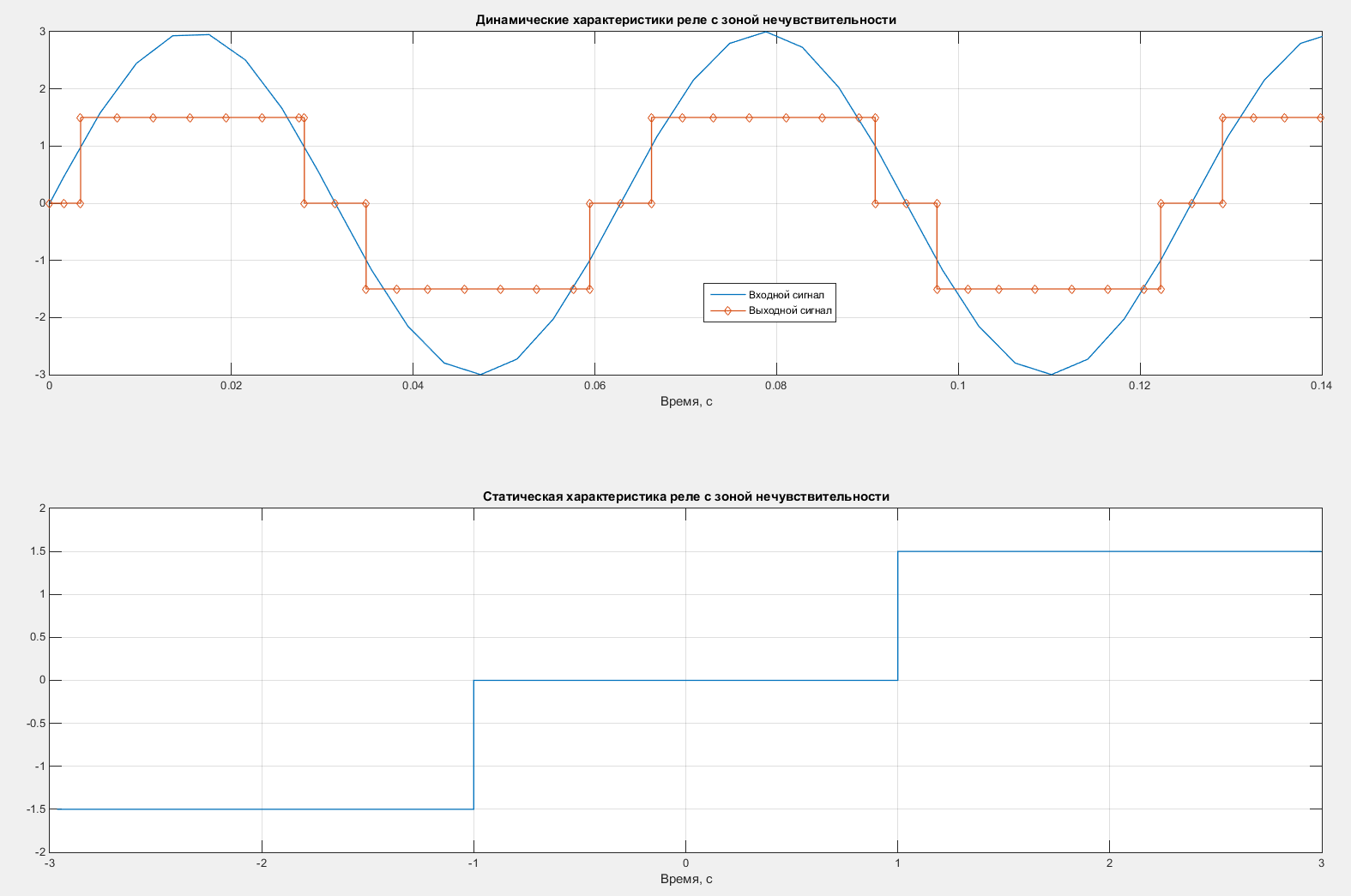
Рисунок 4 – Статические и динамические характеристики реле с зоной нечувствительности
Соберем схему для исследования реле гистерезисного типа. На вход реле подадим сигнал x(t) = 3sin(0.01t) и зафиксируем статические и динамические характеристики элемента. Схема представлена на рисунке 5.
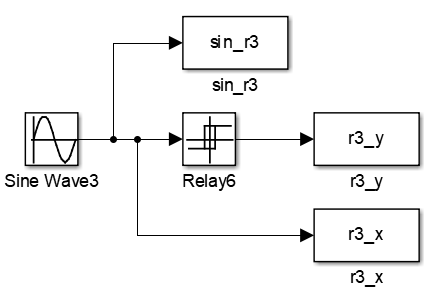
Рисунок 5 – Схема для исследования реле гистерезисного типа
Построим статические и динамические характеристики реле гистерезисного типа. Характеристики представлены на рисунке 6.
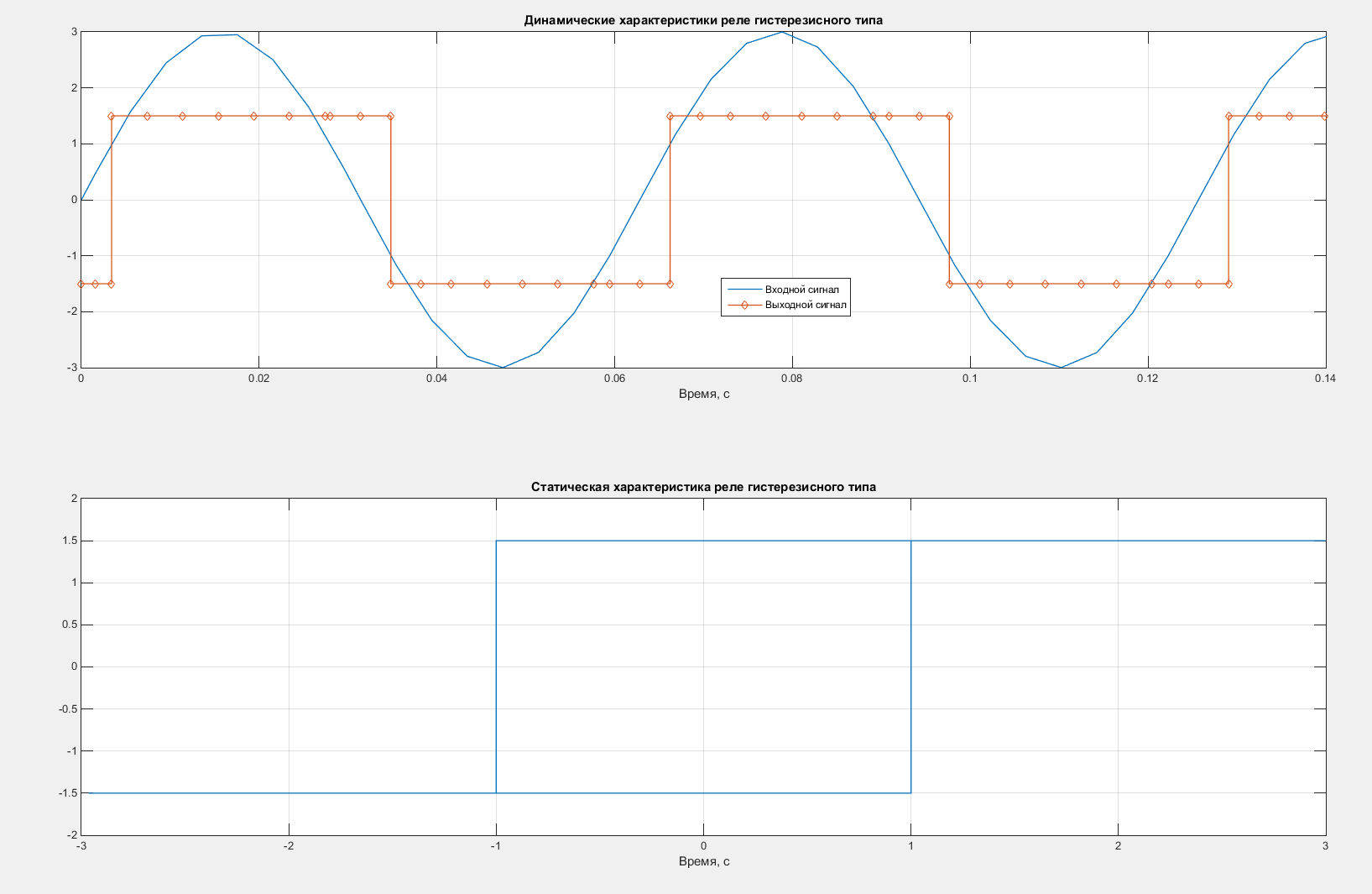
Рисунок 6 – Статические и динамические характеристики реле гистерезисного типа
Соберем схему для исследования реле гистерезисного типа с зоной нечувствительности. На вход реле подадим сигнал x(t) = 3sin(0.01t) и зафиксируем статические и динамические характеристики элемента. Схема представлена на рисунке 7.
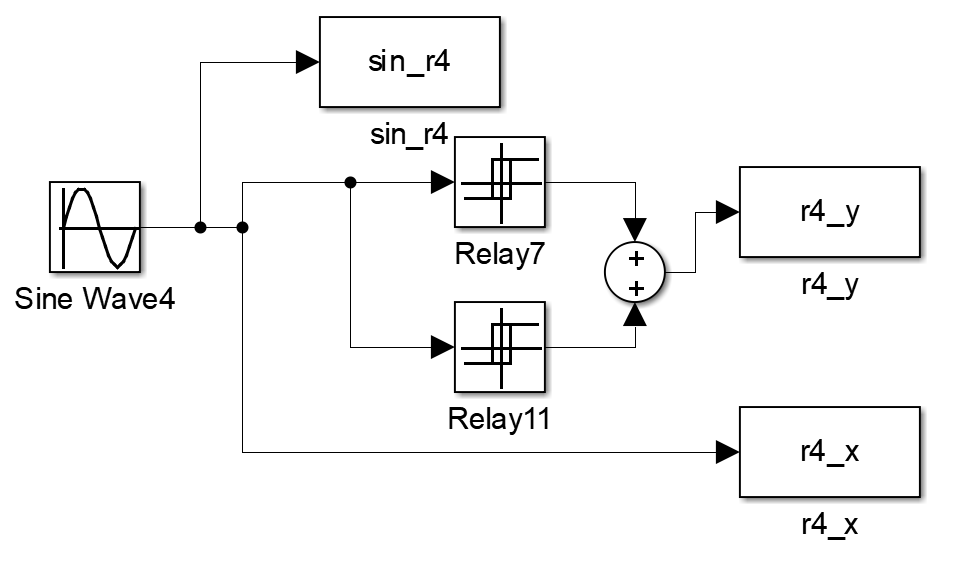
Рисунок 7 – Схема для исследования реле гистерезисного типа с зоной нечувствительности
Построим статические и динамические характеристики реле гистерезисного типа c зоной нечувствительности. Характеристики представлены на рисунке 8.
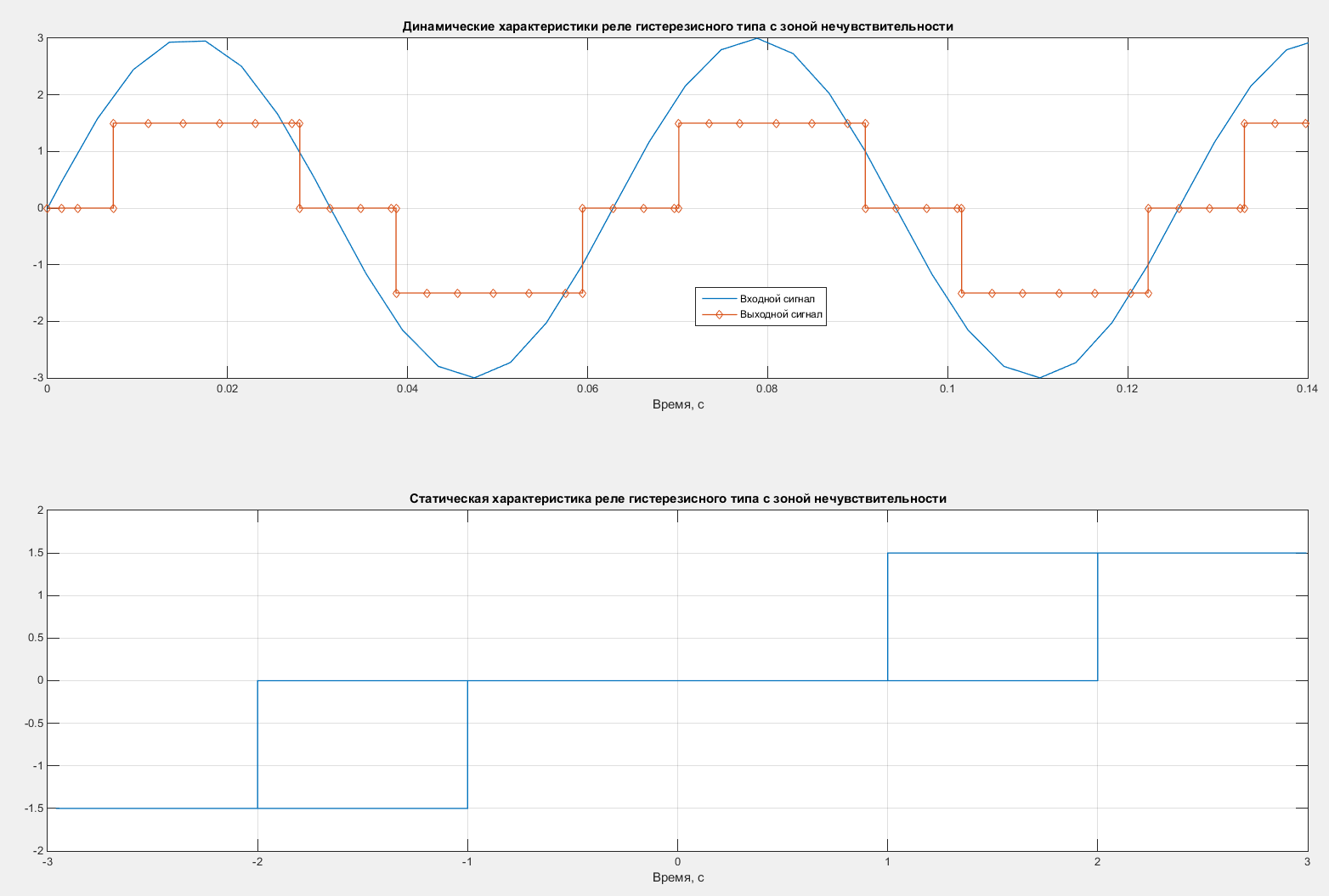
Рисунок 8 – Статические и динамические характеристики реле гистерезисного типа с зоной нечувствительности
Исследование объекта управления вида
Исследование систем с идеальным двухпозиционным реле
Соберем схему системы для случая идеального двухпозиционного реле, отсутствия коррекции по скорости и нулевого входного сигнала. Установим параметры звеньев согласно таблице 1. Схема представлена на рисунке 9.
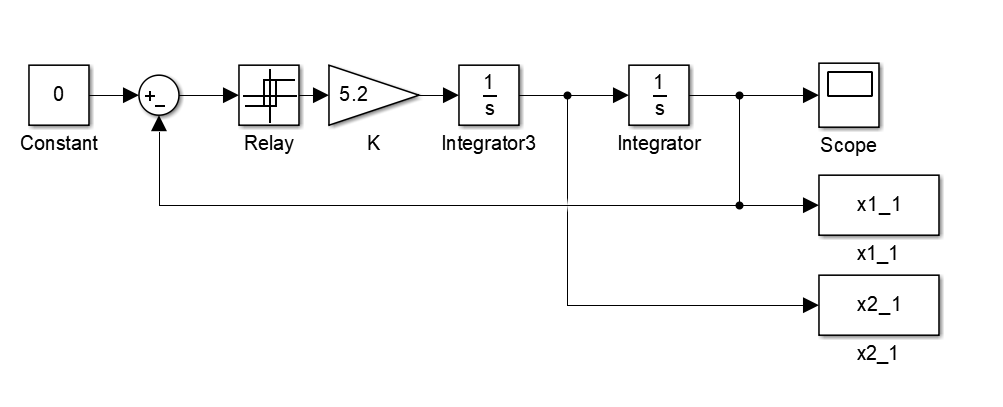
Рисунок 9 – Структурная схема для исследования свободного движения системы
Построим фазовый портрет для случая свободного движения системы. Для этого построим зависимость x20(t) от x10(t). Фазовый портрет представлен на рисунке 10.
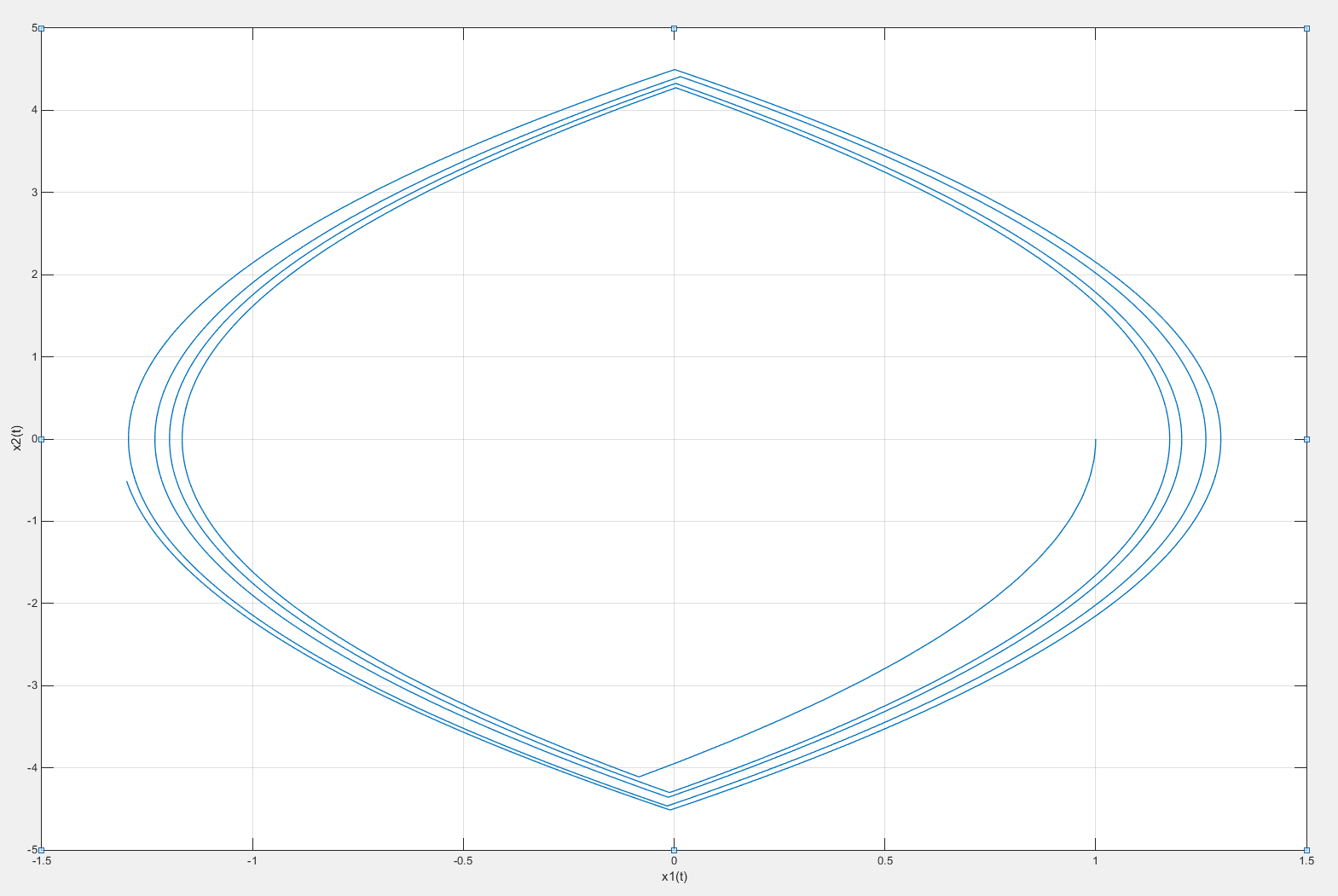
Рисунок 10 – Фазовый портрет свободного движения системы
Графики зависимости x1(t) и x2(t) представлены на рисунке 11.

Рисунок 11 – Графики зависимостей x1(t) и x2(t) в случае свободного движения системы
Введем коррекцию по скорости. Схема с коррекцией по скорости представлена на рисунке 12.
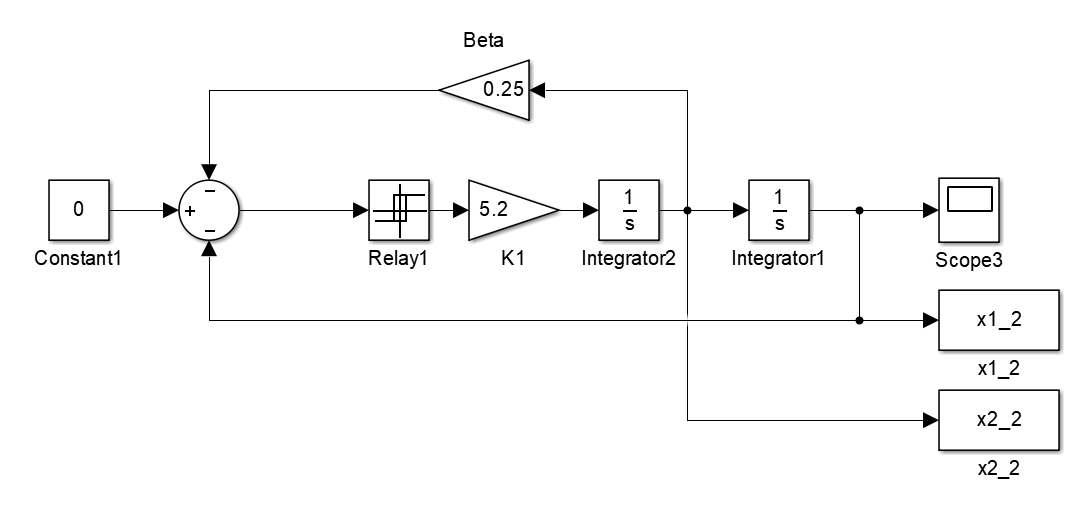
Рисунок 12 – Схема системы с введенной коррекцией по скорости
Зададим коэффициент обратной связи β = 0,25; 0,5; 1 и построим фазовые портреты и графики изменения x1(t) и x2(t) для этих значений коэффициента β. Фазовые портреты, а также графики изменения x1(t) и x2(t) для системы с различными коэффициентами обратной связи представлены на рисунках 13 –18.
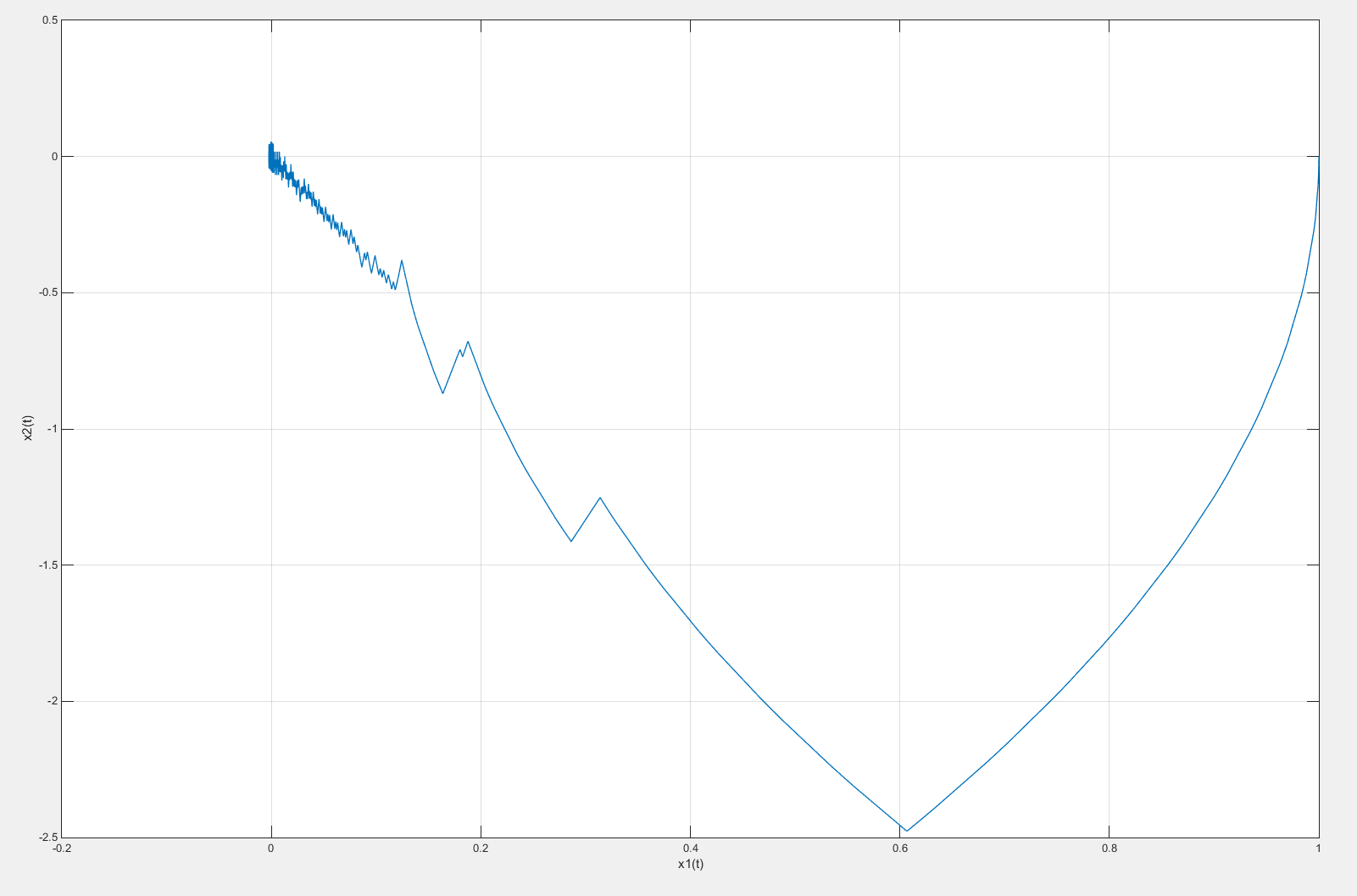
Рисунок 13 – Фазовый портрет системы с введенной коррекцией по скорости с коэффициентом β = 0,25
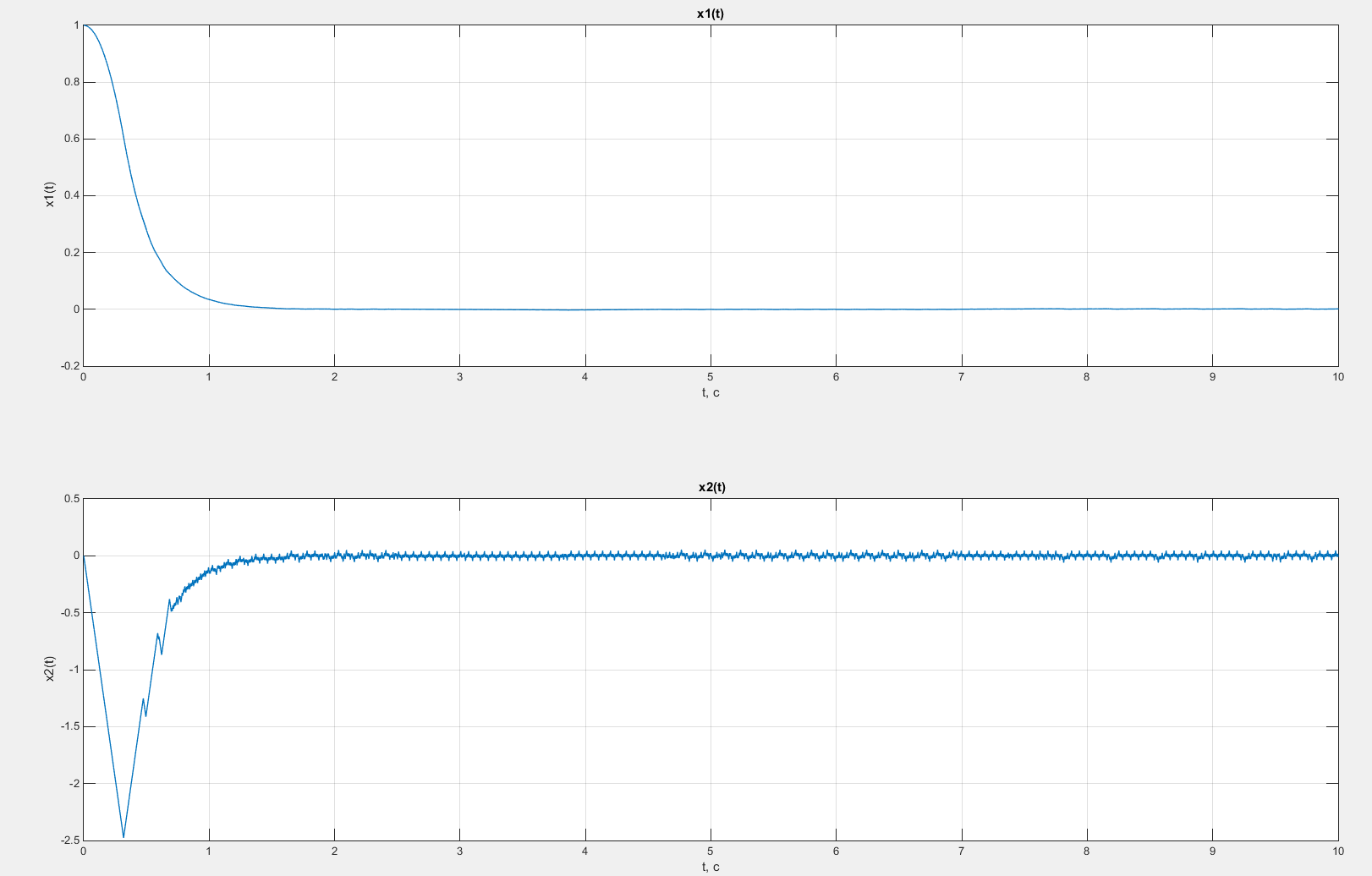
Рисунок 14 – Графики зависимостей x1(t) и x2(t) в случае введения коррекции по скорости с коэффициентом β = 0,25
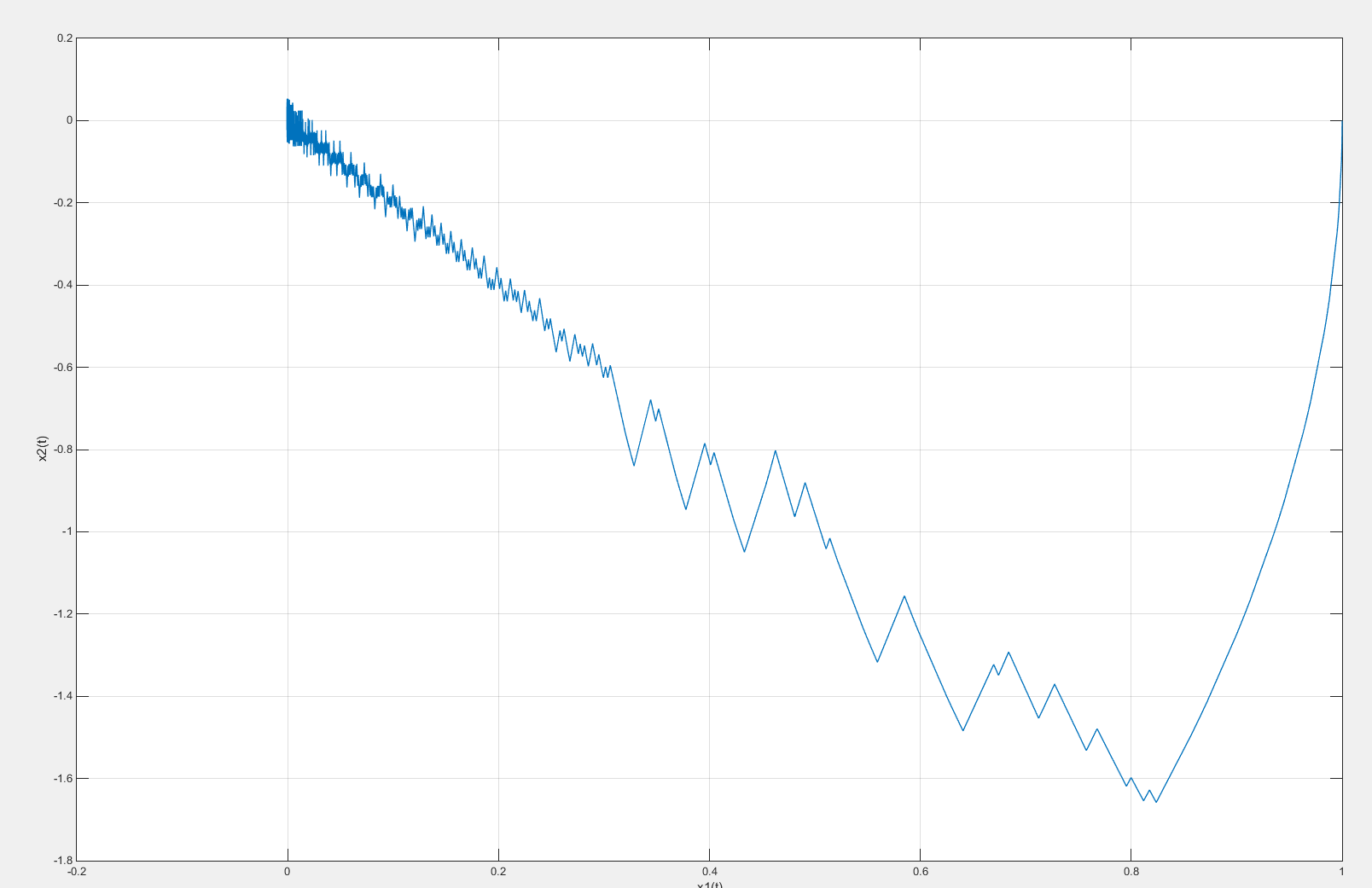
Рисунок 15 – Фазовый портрет системы с введенной коррекцией по скорости с коэффициентом β = 0,5
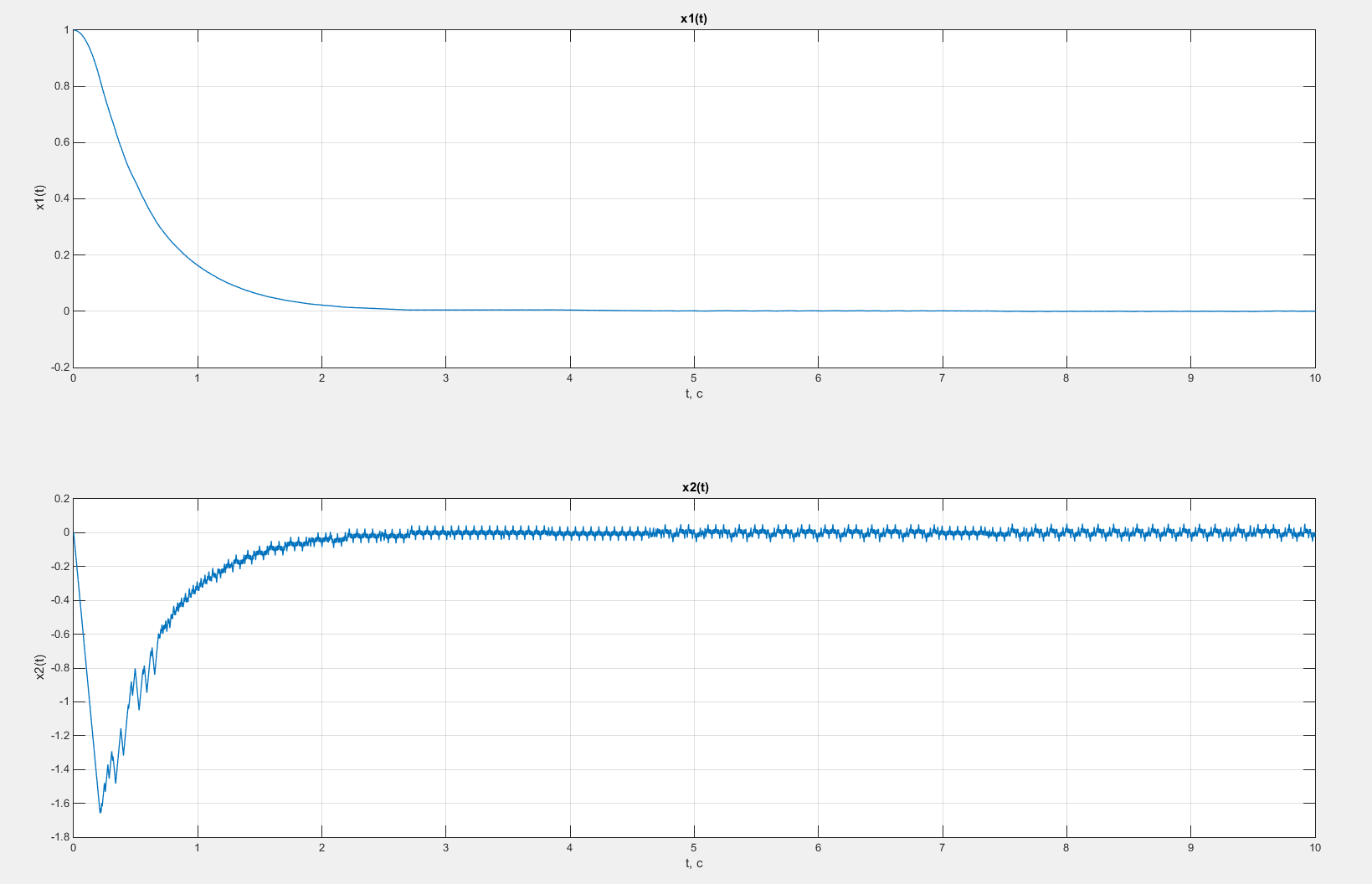
Рисунок 16 – Графики зависимостей x1(t) и x2(t) в случае введения коррекции по скорости с коэффициентом β = 0,5
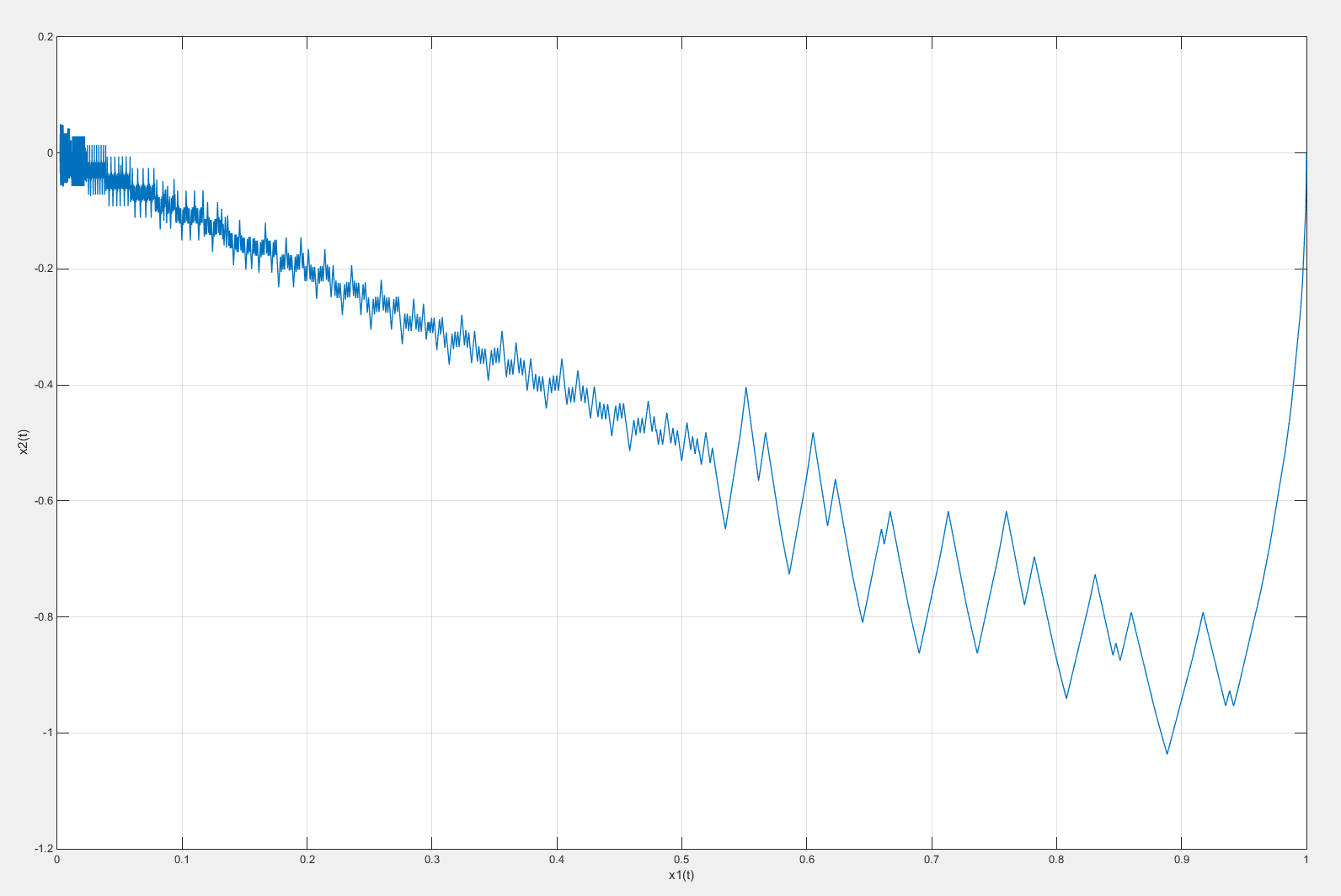
Рисунок 17 – Фазовый портрет системы с введенной коррекцией по скорости с коэффициентом β = 1
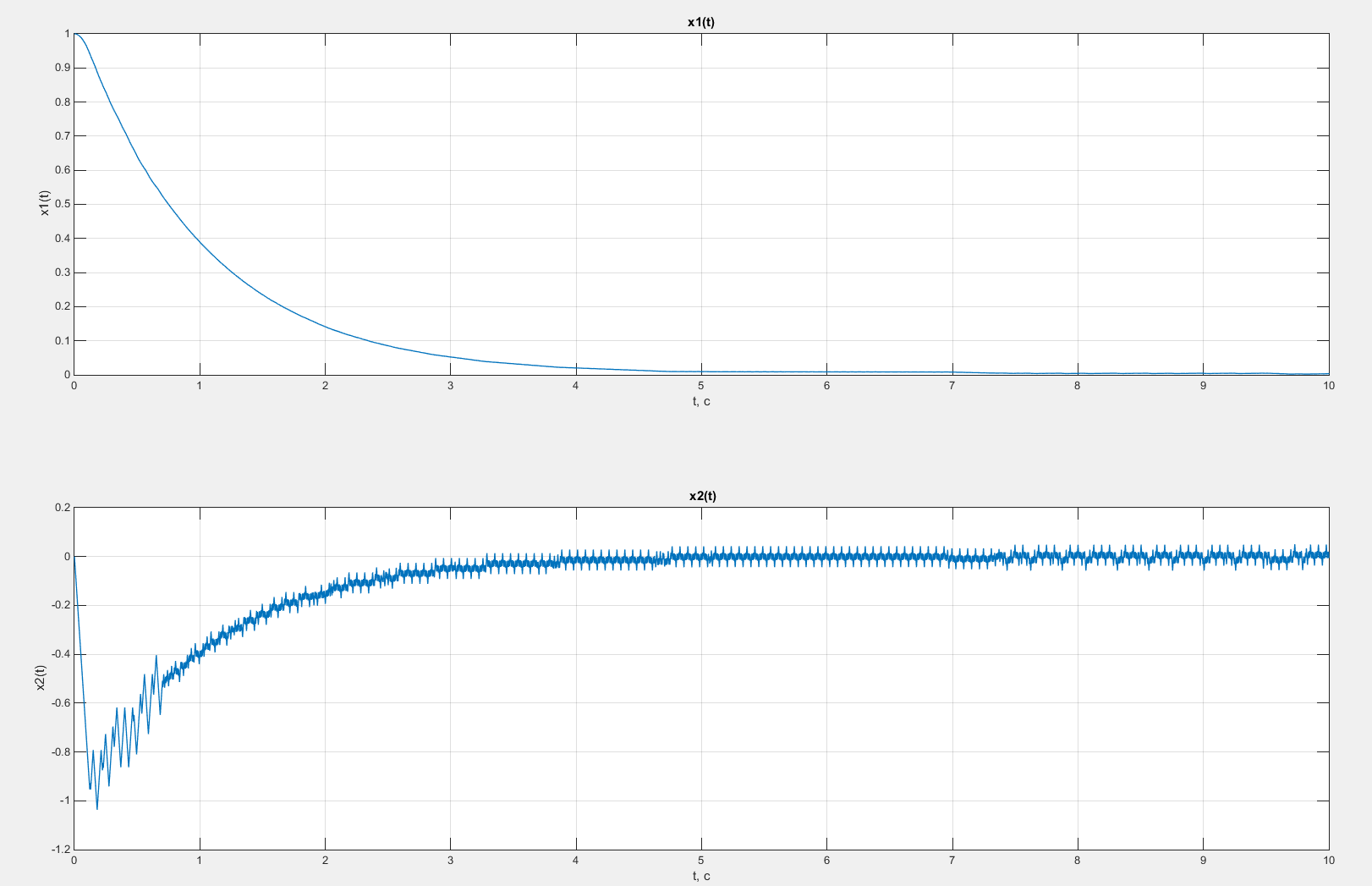
Рисунок 18 – Графики зависимостей x1(t) и x2(t) в случае введения коррекции по скорости с коэффициентом β = 1