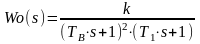Лаба 3 / Лабораторная работа №3_Токарев_0421

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РАПС

отчет

по лабораторной работе № 3

по дисциплине «Теория автоматического управления»

Тема: «Исследование устойчивости линейных систем»

Студент гр. 0421		Токарев А.А.
Преподаватель		Благодарный Н.С.

Санкт-Петербург

2023

Цель работы

Исследование устойчивости замкнутых линейных автоматических систем, определение критических значений параметров систем, построение областей устойчивости.

Ход работы

1. Общие сведения

Исследованию подлежит замкнутая автоматическая система, состоящая из объекта управления с передаточной функцией W_o(s), охваченного отрицательной единичной обратной связью. Передаточная функция объекта W_o(s) указана в таблице 1.

Таблица 1 – Параметры передаточной функции объекта

Вариант	Объект управления Wo(s)	Параметры звена
		k	T1, c	T2, c	Tв, с	T3, c
30		6	3	-	1 – 9	-

2. Исследование устойчивости замкнутой системы по частотным характеристикам разомкнутого контура

Соберем схему объекта управления (разомкнутой системы). Установим параметры звеньев согласно таблице 1. Варьируемую постоянную времени T_в примем наименьшей из диапазона (Т_в = 1 с). Схема представлена на рисунке 1.

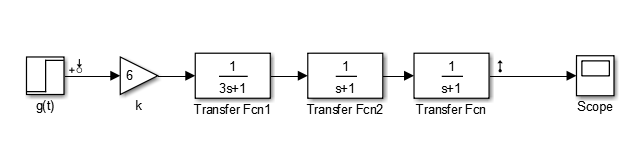
Рисунок 1 – Структурная схема разомкнутой системы

Построим график АФХ разомкнутой системы. Для этого воспользуемся встроенным в MATLAB инструментом Linear Analysis. Он находится в окне Simulink по следующему пути: Analysis → Control Design → Linear Analysis. Выберем точку входа, как Input Perturbation, точку выхода – как Output Measurement. Теперь мы можем построить различные временные и частотные характеристики нашей системы. Построим АФХ, выбрав в графе Plot Result пункт New Nyquist и нажав кнопку Linearize. График АФХ представлен на рисунке 2.

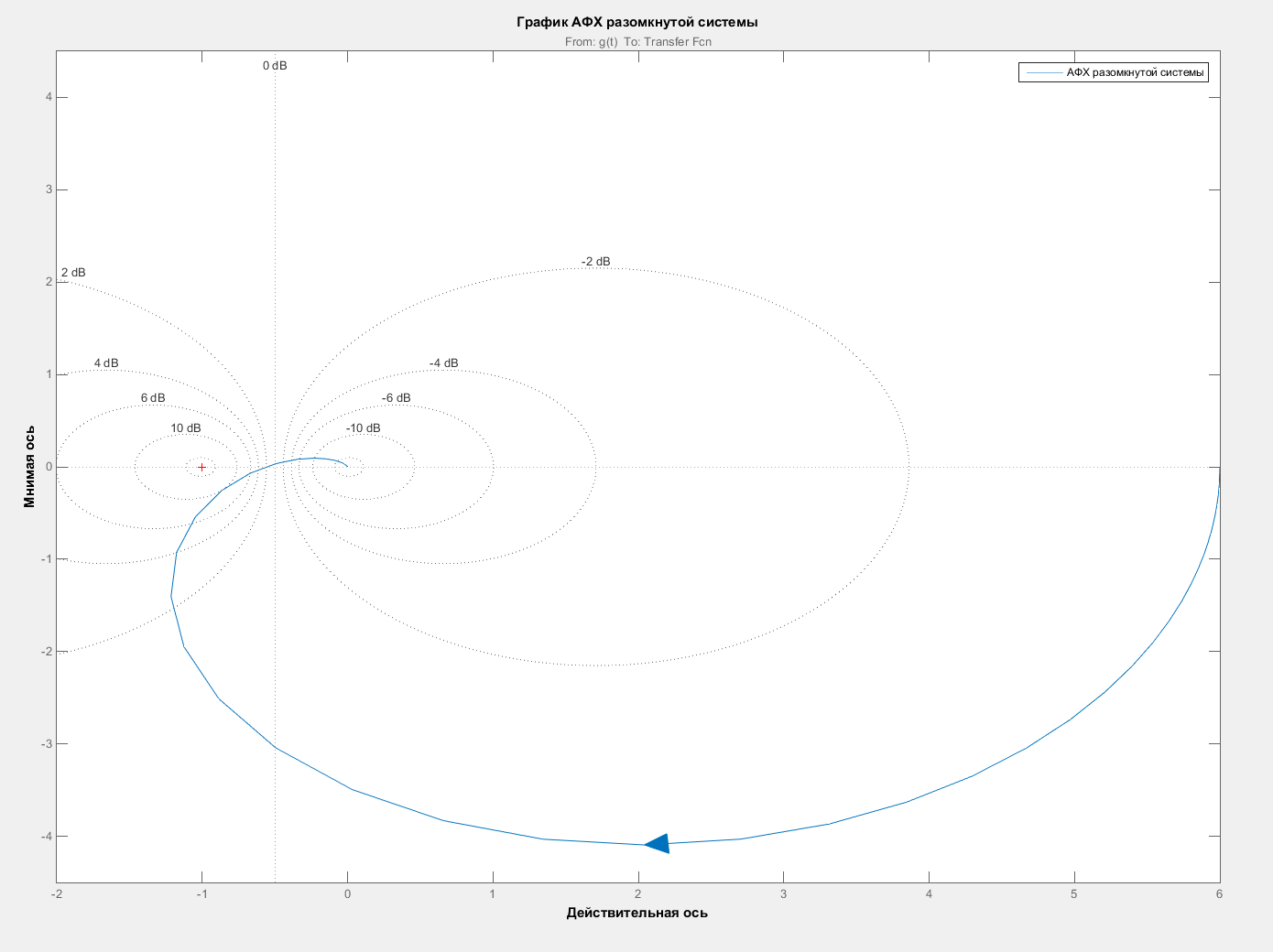
Рисунок 2 – АФХ разомкнутой системы

По виду АФХ, исходя из критерия устойчивости Найквиста, можно сделать вывод, что замкнутая система устойчива, так как АФХ разомкнутой системы не охватывает точку (-1; j0).

Построим графики ЛАХ и ЛФХ разомкнутой системы. Для этого снова воспользуемся встроенным в MATLAB инструментом Linear Analysis. Построим ЛАХ и ЛФХ, выбрав в графе Plot Result пункт New Bode и нажав кнопку Linearize. Графики ЛАХ и ЛФХ представлен на рисунке 3.

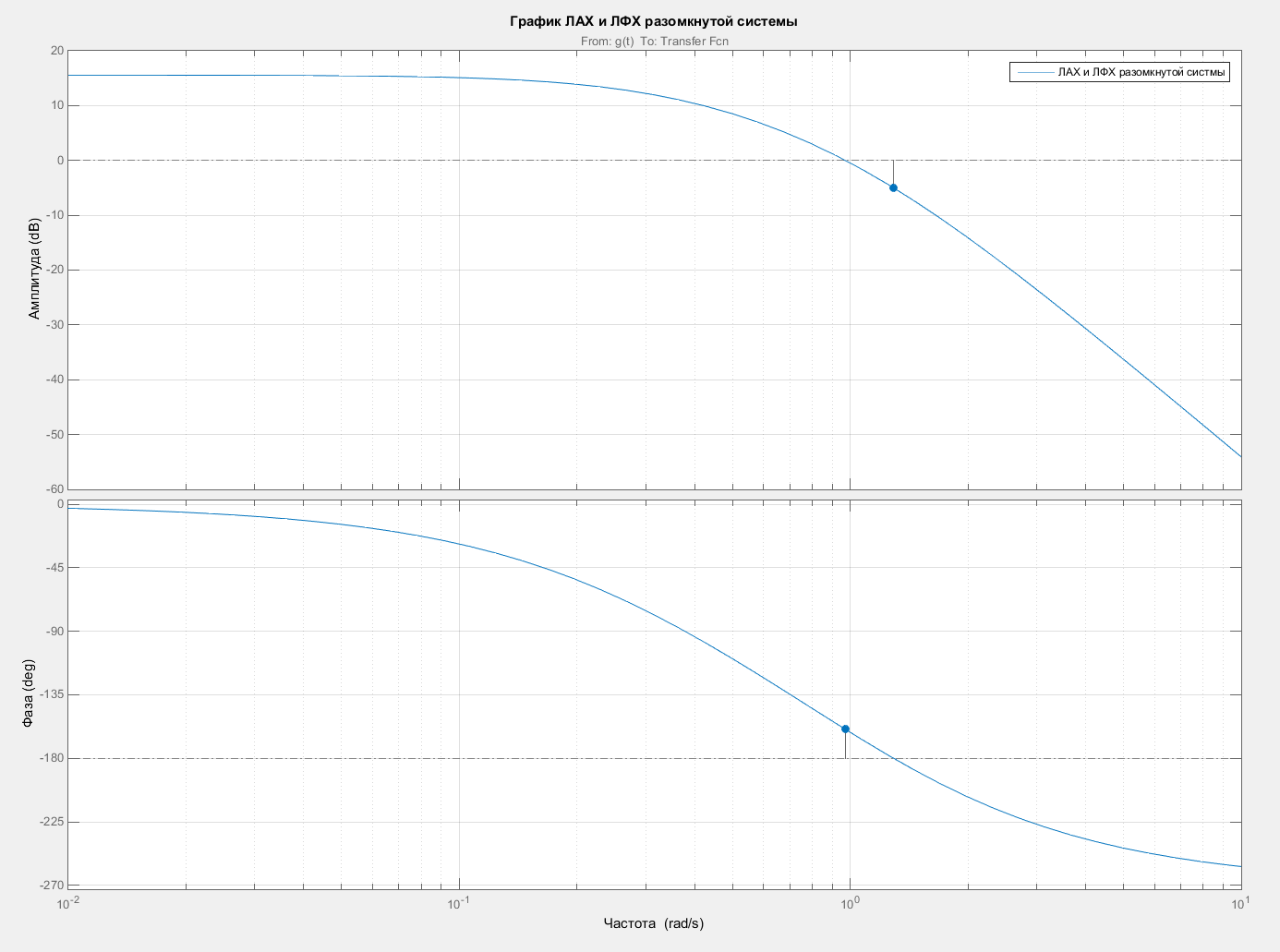
Рисунок 3 – ЛАХ и ЛФХ разомкнутой системы

По виду ЛАХ и ЛФХ, исходя из логарифмического критерия устойчивости, можно сделать вывод, что замкнутая система устойчива, так как точка пересечения ЛАХ с осью абсцисс находится левее точки пересечения ЛФХ с осью –π.

Уменьшим коэффициент усиления объекта в два раза (k = 3). Построим график АФХ для разомкнутой системы с уменьшенным коэффициентом усиления. График АФХ представлен на рисунке 4.

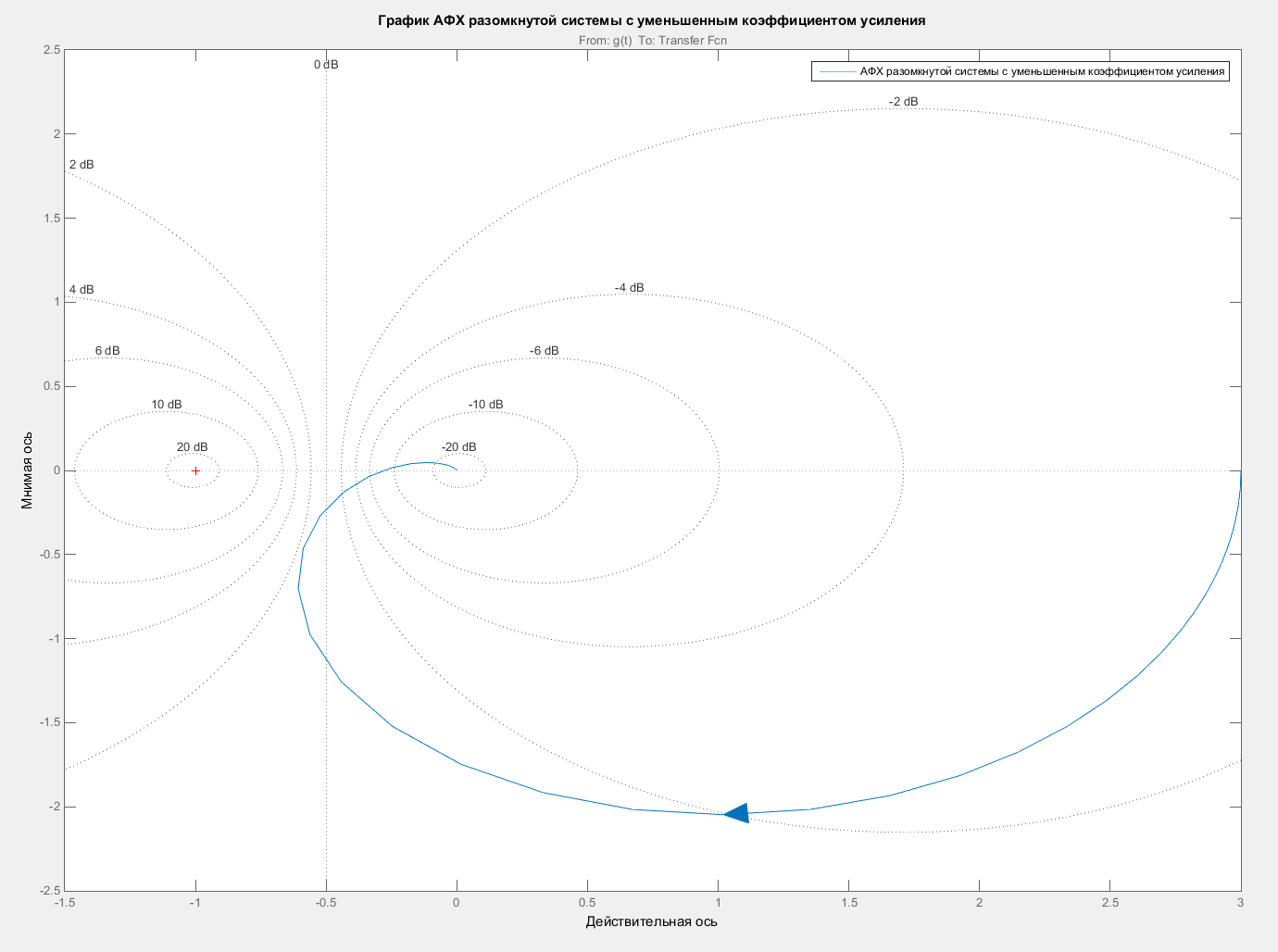
Рисунок 4 – АФХ разомкнутой системы с уменьшенным коэффициентом усиления

По виду АФХ разомкнутой системы с уменьшенным коэффициентом усиления, исходя из критерия устойчивости Найквиста, можно сделать вывод, что замкнутая система устойчива, так как АФХ разомкнутой системы не охватывает точку (-1; j0).

Теперь построим графики ЛАХ и ЛФХ для разомкнутой системы с уменьшенным коэффициентом усиления. Графики ЛАХ и ЛФХ представлены на рисунке 5.

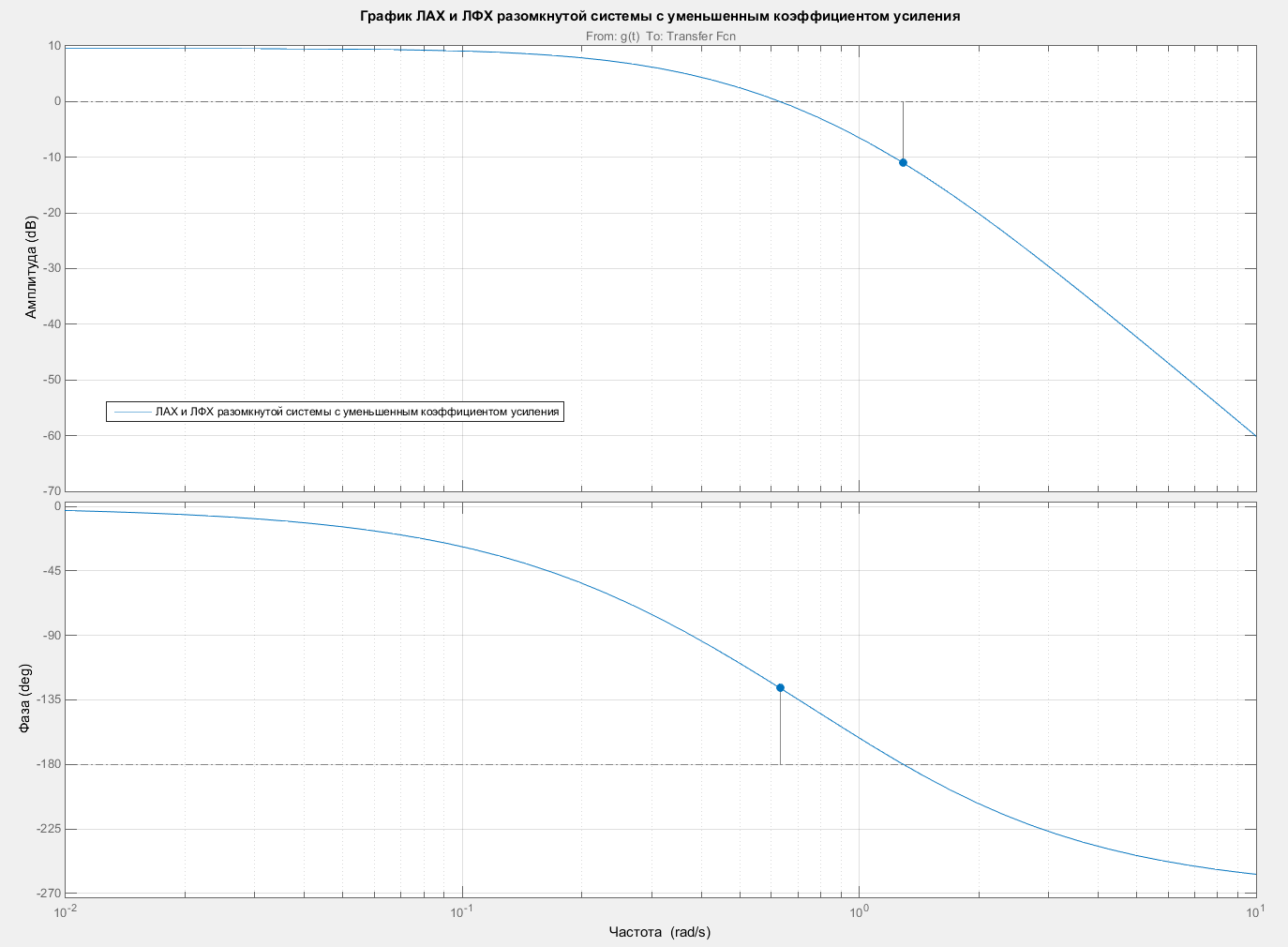
Рисунок 5 – ЛАХ и ЛФХ разомкнутой системы с уменьшенным коэффициентом усиления

По виду ЛАХ и ЛФХ, исходя из логарифмического критерия устойчивости, можно сделать вывод, что замкнутая система устойчива, так как точка пересечения ЛАХ с осью абсцисс находится левее точки пересечения ЛФХ с осью –π.

Как видно из графиков АФХ, ЛАХ и ЛФХ, при уменьшении коэффициента усиления объекта, увеличивается запас устойчивости системы.

3. Исследование замкнутой системы

Замкнем отрицательную обратную связь в системе. Схема замкнутой системы

представлена на рисунке 6. Подадим на вход системы единичное ступенчатое воздействие. Построим переходный процесс в системе, время моделирования выберем 100 с.

Рисунок 6 – Структурная схема замкнутой системы

Построим переходную характеристику замкнутой системы. Переходная характеристика представлена на рисунке 7.

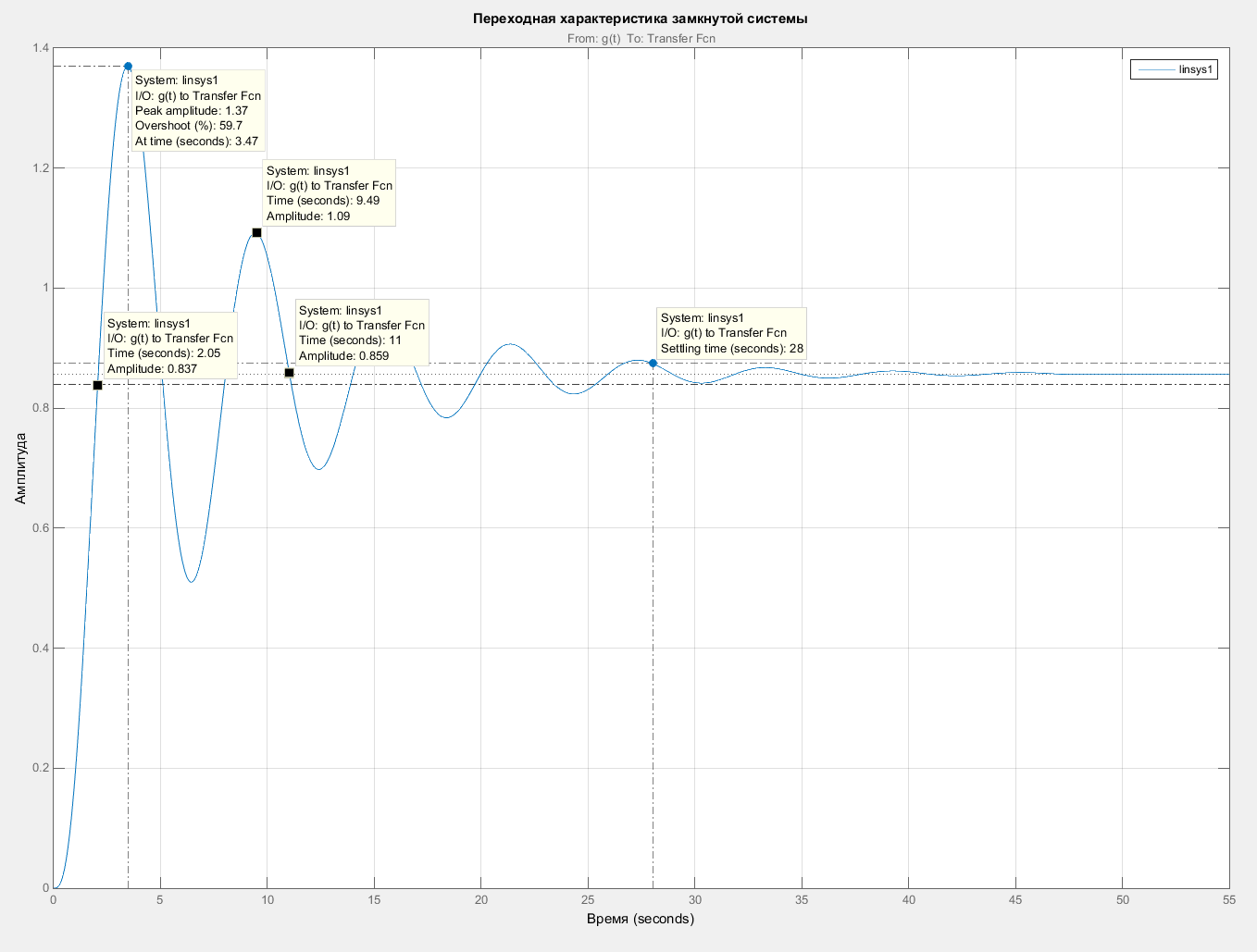
Рисунок 7 – Переходная характеристика замкнутой системы

Оценим устойчивость замкнутой системы. Так как колебания затухают, система является устойчивой. Определим прямые показатели качества регулирования:

1. Время регулирования: t_p = 28 c;

2. Время первого согласования t_1c = 2,05 с;

3. Перерегулирование σ% = 59,7%;

4. Степень затухания переходного процесса ψ =

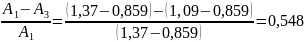
5. Число колебаний переходного процесса k = 4.

4. Построение области устойчивости замкнутой системы

Разомкнем обратную связь в системе и вернемся к схеме, представленной на рисунке 1.

Подберем для установленного минимального значения постоянной времени T_в критическое значение коэффициента передачи контура системы так, чтобы АФХ разомкнутой системы проходила через точку с координатами (-1; j0). Этот случай соответствует нахождению системы на границе устойчивости. График АФХ системы на границе устойчивости при значении постоянной времени Т_в = 1 и коэффициента передачи k = 11 представлен на рисунке 8.

Рисунок 8 – АФХ разомкнутой системы на границе устойчивости

Повторим предыдущий пункт для других четырех значений постоянной времени объекта T_в из диапазона, указанного в таблице 1. Результаты представлены в таблице 2.

Таблица 2 – Протокол определения критических параметров звена

№	Параметр	Критические значения параметров
1	Постоянная времени Tв	1	3	5	7	9
2	Коэффициент усиления k	11	8	8,5	9,3	10,5

Исследуем замкнутую систему на устойчивость с помощью критерия Гурвица. Для этого выпишем характеристический полином замкнутой системы:

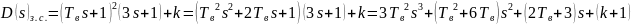
Коэффициенты для составления матрицы Гурвица: а₀ = 3Т²_в, а₁ = Т²_в + 6Т_в,

а₂ = 2Т_в + 3, а₃ = k + 1.

Составим матрицу Гурвица Δ.

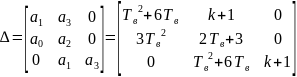
Выпишем главные миноры матрицы Гурвица:

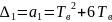
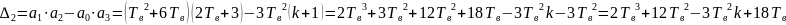
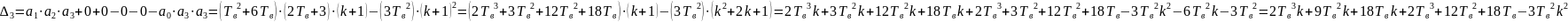
Приравняем последний главный минор матрицы Гурвица к нулю.

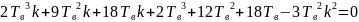
Подставим в полученное уравнение различные значения T_в и решим его относительно k. Пример расчета для Т_в = 1:

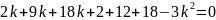
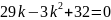
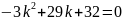
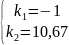
Проведем аналогичные расчеты для всех значений T_в, представленных в таблице 1. Результаты расчета представлены в таблице 3. В качестве критических коэффициентов передачи k взяты положительные решения уравнения.

Таблица 3 - Определение критических параметров звена с помощью критерия Гурвица

№	Параметр	Критические значения параметров
1	Постоянная времени Tв	1	3	5	7	9
2	Коэффициент усиления k	10,67	8	8,53	9,52	10,67

Нанесем на одну графическую область графики, построенные по данным таблиц 2 и 3. Графики представлены на рисунке 9.

Возьмем произвольную точку с целочисленными значениями T_в и k, находящуюся ниже границы устойчивости. Пусть это будет точка с параметрами Т_в = 6, k = 2. Проверим с помощью критерия Гурвица устойчивость замкнутой системы для данной точки. Так как замкнутая система имеет третий порядок, воспользуемся частным случаем критерия Гурвица для системы третьего порядка. Матрица Гурвица для системы в заданной точке будет равна:

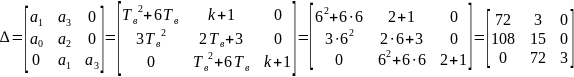
Из частного случая критерия Гурвица для системы третьего порядка известно, что система будет устойчива в случае, если а₁⸱а₂> a₀⸱a₃. Проверим нашу систему:

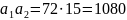
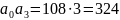
Произведение коэффициентов а₁⸱а₂> a₀⸱a₃, следовательно, система устойчива. Так как система устойчива, то мы можем обозначить на рисунке 9 область устойчивости системы.

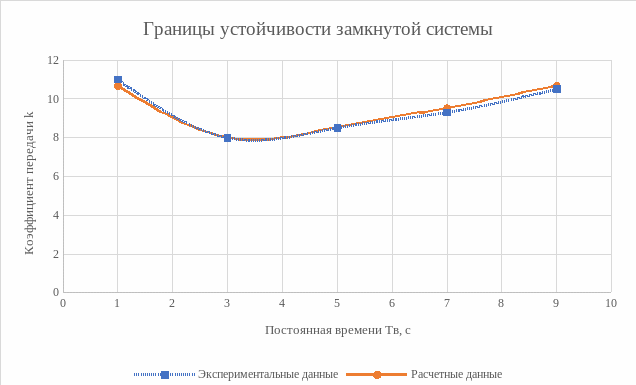
Рисунок 9 – Границы устойчивости замкнутой системы

Вывод

В данной лабораторной работе была исследована устойчивость замкнутой системы управления. В среде Simulink устойчивость замкнутой системы была исследована с помощью частотного критерия устойчивости Найквиста и с помощью логарифмического критерия устойчивости. Исследуемая замкнутая система является устойчивой. Были построены АФХ, ЛАХ и ЛФХ разомкнутой системы при различных коэффициентах передачи системы, показано, что при уменьшении коэффициента передачи системы в 2 раза запасы устойчивости замкнутой системы увеличиваются. Была определена экспериментальная граница устойчивости.

Кроме того, была построена переходная характеристика замкнутой системы, определены прямые показатели качества регулирования: t_p = 28 c; t_1c = 2,05 с; σ% = 59,7%; ψ = 0,548; k = 4. Качество регулирования оказалось достаточно низким, если сравнивать с прямыми показателями регулирования общепромышленных систем.

Также был применен численный критерий устойчивости Гурвица для замкнутой системы. Была определена расчетная граница устойчивости замкнутой системы, построен график экспериментальной и расчетной границ устойчивости, определена область устойчивости замкнутой системы. Экспериментальное определение границы устойчивости оказалось менее точным, чем расчетное, но незначительно (разница ~1-2%).