
- •Лабораторная работа №3
- •3. Исследование устойчивости линейных систем
- •3.1. Цель работы:
- •3.2. Описание объекта исследования
- •3.3. Задание на работу
- •3.4. Указания по выполнению работы
- •3.5. Порядок выполнения работы
- •3.5.1. Исследование устойчивости замкнутой системы по частотным характеристикам разомкнутого контура
- •3.5.2. Исследование замкнутой системы
- •3.5.3. Построение области устойчивости замкнутой системы
- •Требования к оформлению отчета
- •Вопросы для самопроверки
Лабораторная работа №3
3. Исследование устойчивости линейных систем
3.1. Цель работы:
Исследование устойчивости замкнутых линейных автоматических систем, определение критических значений параметров систем, построение областей устойчивости.
3.2. Описание объекта исследования
Исследованию подлежит замкнутая автоматическая система, состоящая из объекта управления с передаточной функцией Wo(s), охваченного отрицательной единичной обратной связью. Передаточная функция объекта Wo(s) указана в табл. 3.1.
3.3. Задание на работу
Построить АФХ разомкнутого контура системы и исследовать устойчивость замкнутой автоматической системы с помощью критерия Найквиста при разных значениях коэффициента передачи разомкнутого контура (объекта).
Построить ЛАХ и ЛФХ разомкнутого контура системы и исследовать устойчивость замкнутой автоматической системы с помощью логарифмического критерия при разных значениях коэффициента передачи разомкнутого контура.
Построить переходные характеристики замкнутой системы при различных значениях коэффициента передачи разомкнутого контура и по виду переходных характеристик оценить устойчивость замкнутой системы и показатели качества регулирования.
Для пяти различных значений варьируемой постоянной времени объекта TB из диапазона, указанного в табл.3.1, подобрать такие значения коэффициента передачи k , при которых АФХ разомкнутого контура системы Wo(jw) проходит через точку с координатами (-1; j0), т.е. система находится на границе устойчивости. Построить границу устойчивости замкнутой системы в плоскости параметров k и TB и отметить область устойчивости.
С помощью критерия Гурвица построить границу устойчивости замкнутой системы в плоскости параметров k и TB . Сравнить границы устойчивости, построенные в п.4 и 5.
3.4. Указания по выполнению работы
Лабораторная работа выполняется в программном комплексе "Анализ систем 3.1" или .MATLAB.
Все схемы и графики следует сохранять в Вашем файле текстового редактора Word и снабжать комментариями.
Варианты заданий приведены в таблице 3.1.
3.5. Порядок выполнения работы
3.5.1. Исследование устойчивости замкнутой системы по частотным характеристикам разомкнутого контура
Загрузить программу Syan. Собрать в поле редактора схему объекта управления (разомкнутой системы). В качестве примера на рис.3.1 показана структурная схема объекта управления для 7 – 9 вариантов. Обозначить вход и выход объекта щелчком правой кнопки мыши, как показано на рисунке.
![]()
Рис.3.1. Структурная схема объекта управления.
Установить параметры объекта в соответствии с Вашим вариантом. Коэффициент передачи одного из звеньев объекта установить, равным значению k из табл.3.1, а коэффициенты передач других звеньев, равными 1. Постоянные времени звеньев установить в соответствии с вашим вариантом из таблицы. Варьируемую постоянную времени объекта TB принять наименьшей из диапазона, указанного в табл.3.1
Табл.3.1.
№ вар |
Объект управления Wo(s) |
Параметры звена |
||||
k |
T1, с |
T2 , с |
TB, с |
T3, с |
||
1 |
|
5 |
4 |
5 |
2 – 10 |
- |
2 |
12 |
0,5 |
0,5 |
0,2 – 1,4 |
- |
|
3 |
18 |
1 |
0,4 |
0,1 – 0,5 |
- |
|
4 |
10 |
2 |
2 |
3-7 |
- |
|
5 |
|
15 |
0,05 |
0,5 |
0,3 – 1,4 |
05 |
6 |
10 |
0,04 |
1,5 |
1 – 9 |
3 |
|
7 |
15 |
0,1 |
0,7 |
0,5 – 4 |
1,5 |
|
8 |
20 |
0,08 |
1 |
0,5-6,5 |
2 |
|
9 |
|
4 |
0,02 |
0,5 |
1 – 5 |
- |
10 |
0,5 |
3 |
13 |
10 – 50 |
- |
|
11 |
10 |
0,01 |
0,2 |
0,1 – 0,5 |
- |
|
12 |
1 |
0,2 |
6 |
2 – 10 |
- |
|
13 |
|
5 |
3 |
- |
0,1 – 0,5 |
|
14 |
7 |
0,7 |
- |
0,01 – 0,1 |
|
|
15 |
10 |
10 |
- |
0,5 – 2 |
|
|
16 |
10 |
5 |
- |
0,2 – 1 |
|
|
17 |
|
6 |
0,05 |
0,05 |
1 – 5 |
0,5 |
18 |
2 |
0,04 |
1,5 |
3 – 7 |
5 |
|
19 |
3 |
0,1 |
0,7 |
10 – 50 |
1,5 |
|
20 |
3 |
0,08 |
1 |
5 – 25 |
2 |
|
21 |
|
0,2 |
4 |
1 |
10 – 30 |
- |
22 |
3 |
0,5 |
0,5 |
2 – 4 |
- |
|
23 |
8 |
1 |
0,4 |
5 – 25 |
- |
|
24 |
10 |
0,2 |
0,2 |
0,5 – 1 |
- |
|
25 |
|
20 |
0,01 |
1 |
0,1 – 0,5 |
1 |
26 |
20 |
0,1 |
0,5 |
0,6 – 1,4 |
0,5 |
|
27 |
18 |
0,04 |
0,8 |
0,5 – 6,5 |
2,5 |
|
28 |
40 |
0,4 |
1,2 |
1,5 – 2 |
1,5 |
|
29 |
|
16 |
0,02 |
- |
0,1 – 0,5 |
- |
30 |
6 |
3 |
- |
1 – 9 |
- |
|
31 |
9 |
0,5 |
- |
0,1 – 3,7 |
- |
|
32 |
14 |
0,2 |
- |
0,05 – 0,5 |
- |
|
33 |
|
7 |
0,05 |
5 |
2 – 10 |
- |
34 |
12 |
0,04 |
0,5 |
0,2 – 1,8 |
- |
|
35 |
30 |
0,1 |
0,2 |
0,8 – 1,6 |
- |
|
36 |
15 |
0,08 |
2 |
1 – 5 |
- |
|
37 |
|
1,5 |
0,02 |
- |
2 – 7 |
- |
38 |
9 |
0,2 |
- |
0,6 – 1,8 |
- |
|
39 |
1,5 |
0,01 |
- |
1 – 5 |
- |
|
40 |
3 |
2 |
- |
5 – 20 |
- |
|
41 |
|
0,7 |
2 |
0,2 |
0,3 – 3 |
- |
42 |
0,2 |
0,7 |
1,5 |
0,8 – 1,8 |
- |
|
43 |
1,5 |
0,2 |
0,7 |
3 – 7 |
- |
|
44 |
1 |
2 |
0,5 |
7 – 10 |
- |
|
45 |
|
6 |
0,5 |
- |
0,3 – 1,4 |
- |
46 |
10 |
1,5 |
- |
1 – 9 |
- |
|
47 |
7 |
0,7 |
- |
0,5 – 1 |
- |
|
48 |
5 |
4 |
- |
2 – 7 |
- |
|
49 |
|
20 |
0,5 |
- |
2 – 10 |
- |
50 |
12 |
1,5 |
- |
20 – 70 |
- |
|
51 |
18 |
0,1 |
- |
1 – 10 |
- |
|
52 |
16 |
1 |
- |
5 – 9 |
- |
|
53 |
|
7 |
0,3 |
0,02 |
5 – 9 |
- |
54 |
10 |
0,1 |
0,3 |
10 – 50 |
- |
|
55 |
17 |
0,04 |
0,01 |
0,5 – 5 |
- |
|
56 |
30 |
0,2 |
0,2 |
2 – 30 |
- |
|
57 |
|
10 |
4 |
5 |
0,01 – 0,5 |
- |
58 |
5 |
0,5 |
0,5 |
0,01 – 0,1 |
- |
|
59 |
15 |
1 |
0,4 |
0,1 – 0,2 |
- |
|
60 |
10 |
2 |
10 |
0,1 – 0,5 |
- |
|
Сохранить схему с комментарием в Вашем текстовом файле редактора Word.
Построить график АФХ разомкнутой системы. При построении графика подобрать диапазон частот так, чтобы было видно, охватывает ли АФХ точку с координатами (-1;j0).
Сделать суждение об устойчивости замкнутой системы, скопировать график АФХ в Ваш текстовый файл и снабдить комментарием об ее устойчивости или неустойчивости. На рис.3.2 замкнутая система неустойчива, т.к. АФХ ее разомкнутого контура охватывает точку (-1;j0).
П
 остроить
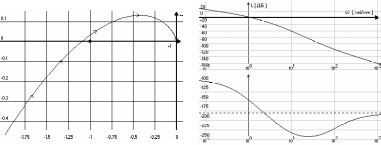
графики ЛАХ и ЛФХ разомкнутой системы
(см. рис. 3.3), скопировать их в Ваш текстовый
файл и снабдить комментарием. На рис.
3.3 замкнутая система устойчива, т.к.
остроить
графики ЛАХ и ЛФХ разомкнутой системы
(см. рис. 3.3), скопировать их в Ваш текстовый
файл и снабдить комментарием. На рис.
3.3 замкнутая система устойчива, т.к.
Рис.3.2. АФХ разомкнутой системы. Рис.3.3. ЛАХ и ЛФХ разомкнутой системы.
точка пересечения ЛАХ с осью абсцисс находится левее точки пересечения ЛФХ с осью –180 о.
Изменить коэффициент усиления объекта (увеличить или уменьшить в 2 раза) и повторить пп. 4 - 6. В комментариях указать новое значение коэффициента усиления звена и вывод об устойчивости системы.
