Лаба 2 / Лабораторная работа №2_Токарев_0421

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РАПС

отчет

по лабораторной работе № 2

по дисциплине «Теория автоматического управления»

Тема: «Исследование влияния степени астатизма на значение установившейся ошибки САУ»

Студент гр. 0421		Токарев А.А.
Преподаватель		Благодарный Н.С.

Санкт-Петербург

2023

Цель работы

Исследование влияния степени астатизма системы на значение установившейся ошибки регулирования при различных входных воздействиях.

Ход работы

1. Общие сведения

В качестве объекта управления будем рассматривать звено с передаточной функцией 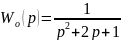. В качестве возмущающего воздействия будем рассматривать единичное ступенчатое воздействие c временем запаздывания в 1 секунду: .

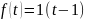2. Исследование САУ с нулевым порядком астатизма

Соберем схему системы с нулевым порядком астатизма. Схема представлена на рисунке 1.

Рисунок 1 – Структурная схема системы с астатизмом 0 порядка

Рассмотрим случай задающего воздействия 0 порядка. В качестве задающего воздействия будем рассматривать единичное ступенчатое воздействие c временем запаздывания в 1 секунду: 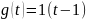. Графики задающего воздействия, регулируемой переменной и ошибки представлены на рисунке 2.

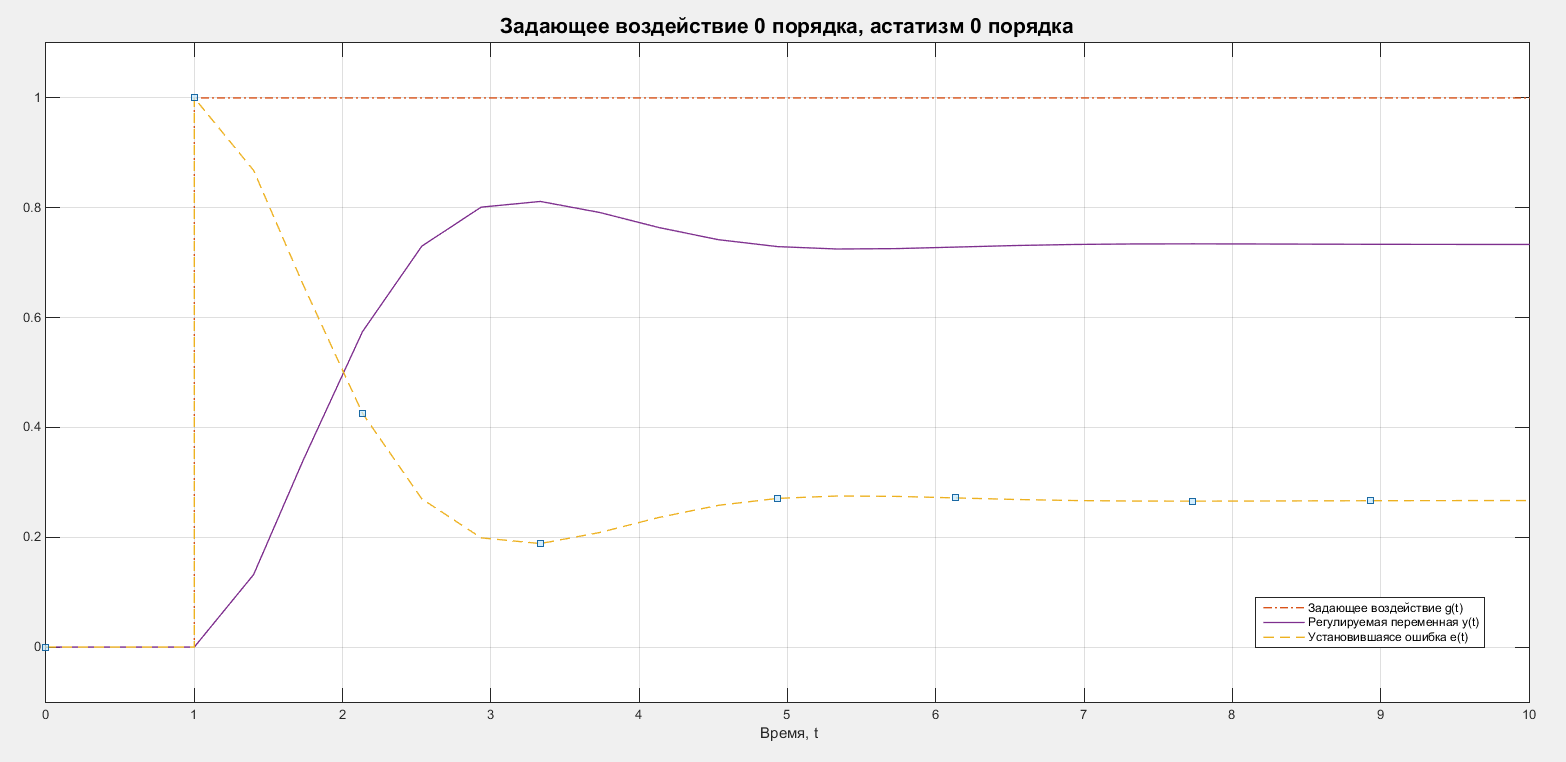
Рисунок 2 – Графики для системы с 0 порядком астатизма и воздействия 0 порядка.

Рассмотрим случай задающего воздействия 1 порядка. В качестве задающего воздействия будем рассматривать функцию единичного наклона: 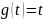. Графики задающего воздействия, регулируемой переменной и ошибки представлены на рисунке 3.

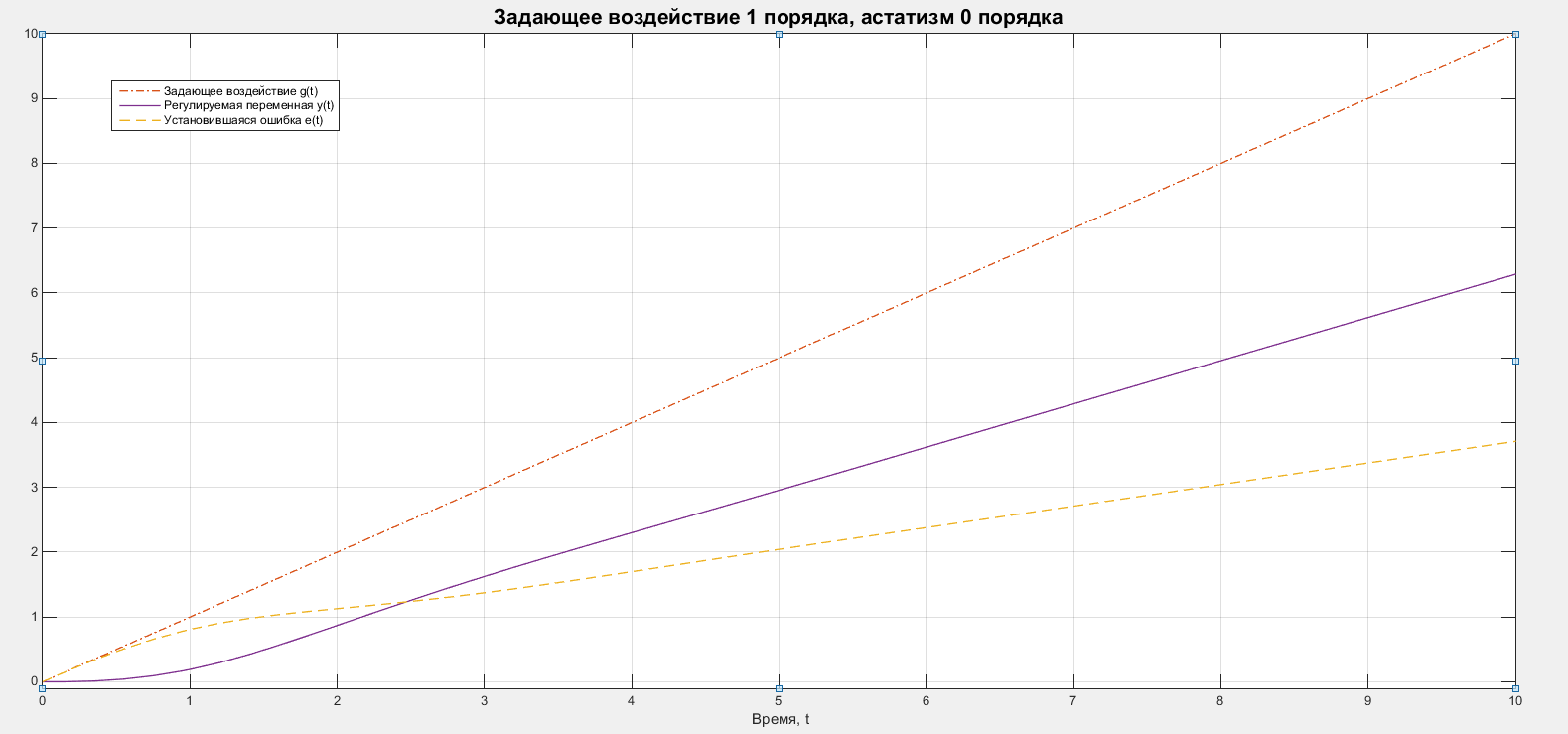
Рисунок 3 – Графики для системы с 0 порядком астатизма и воздействия 1 порядка

Рассмотрим случай задающего воздействия 2 порядка. В качестве задающего воздействия будем рассматривать квадратичную функцию: 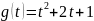. Графики задающего воздействия, регулируемой переменной и ошибки представлены на рисунке 4.

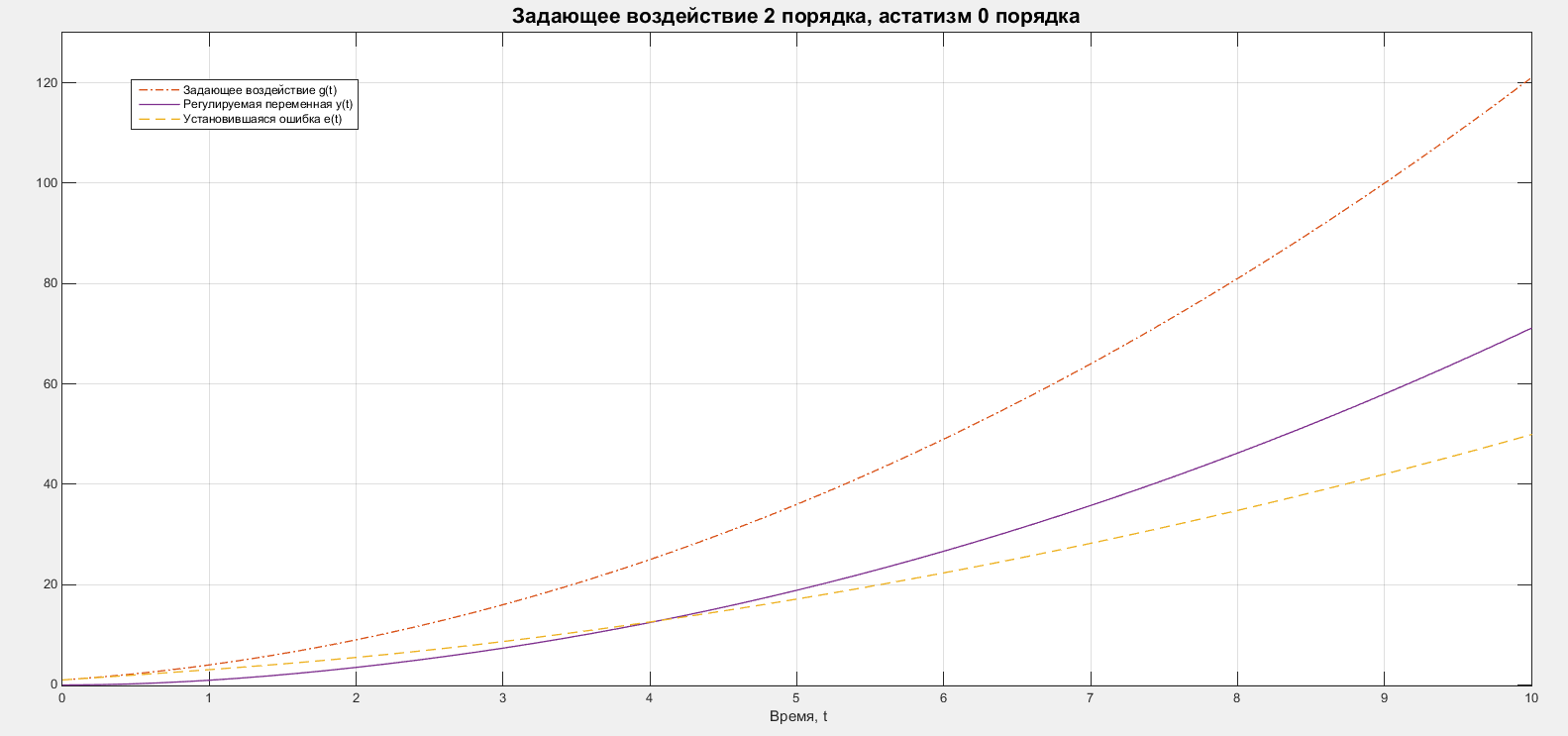
Рисунок 4 – Графики для системы с 0 порядком астатизма и воздействия 2 порядка.

3. Исследование САУ с первым порядком астатизма

Соберем схему системы с первым порядком астатизма. Схема представлена на рисунке 5.

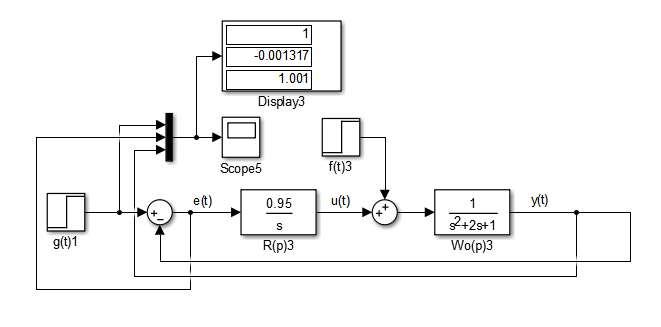Рисунок 5 – Структурная схема системы с астатизмом 1 порядка

Рассмотрим случай задающего воздействия 0 порядка. В качестве задающего воздействия будем рассматривать единичное ступенчатое воздействие c временем запаздывания в 1 секунду: . Графики задающего воздействия, регулируемой переменной и ошибки представлены на рисунке 6.

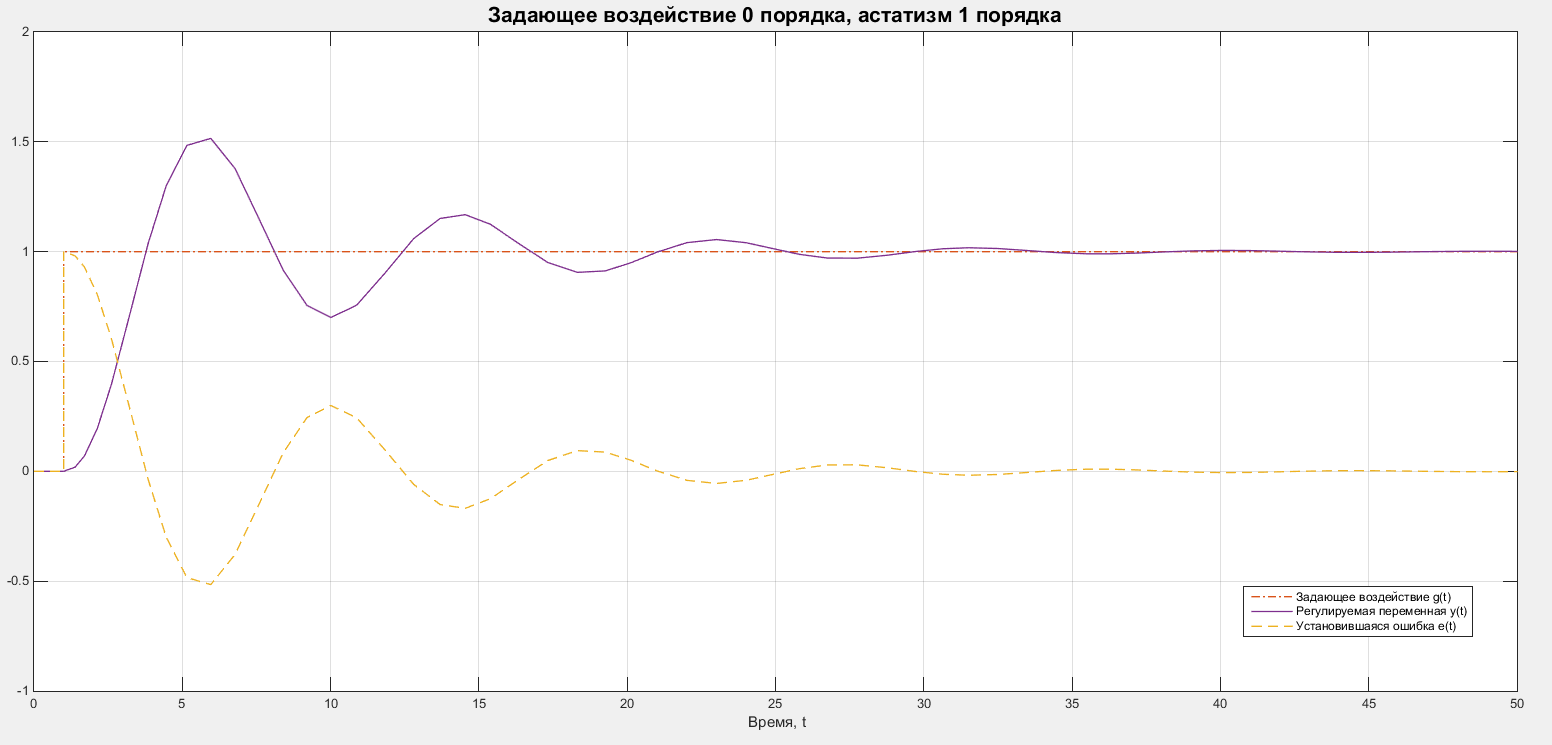
Рисунок 6 – Графики для системы с 1 порядком астатизма и воздействия 0 порядка.

Рассмотрим случай задающего воздействия 1 порядка. В качестве задающего воздействия будем рассматривать функцию единичного наклона: . Графики задающего воздействия, регулируемой переменной и ошибки представлены на рисунке 7.

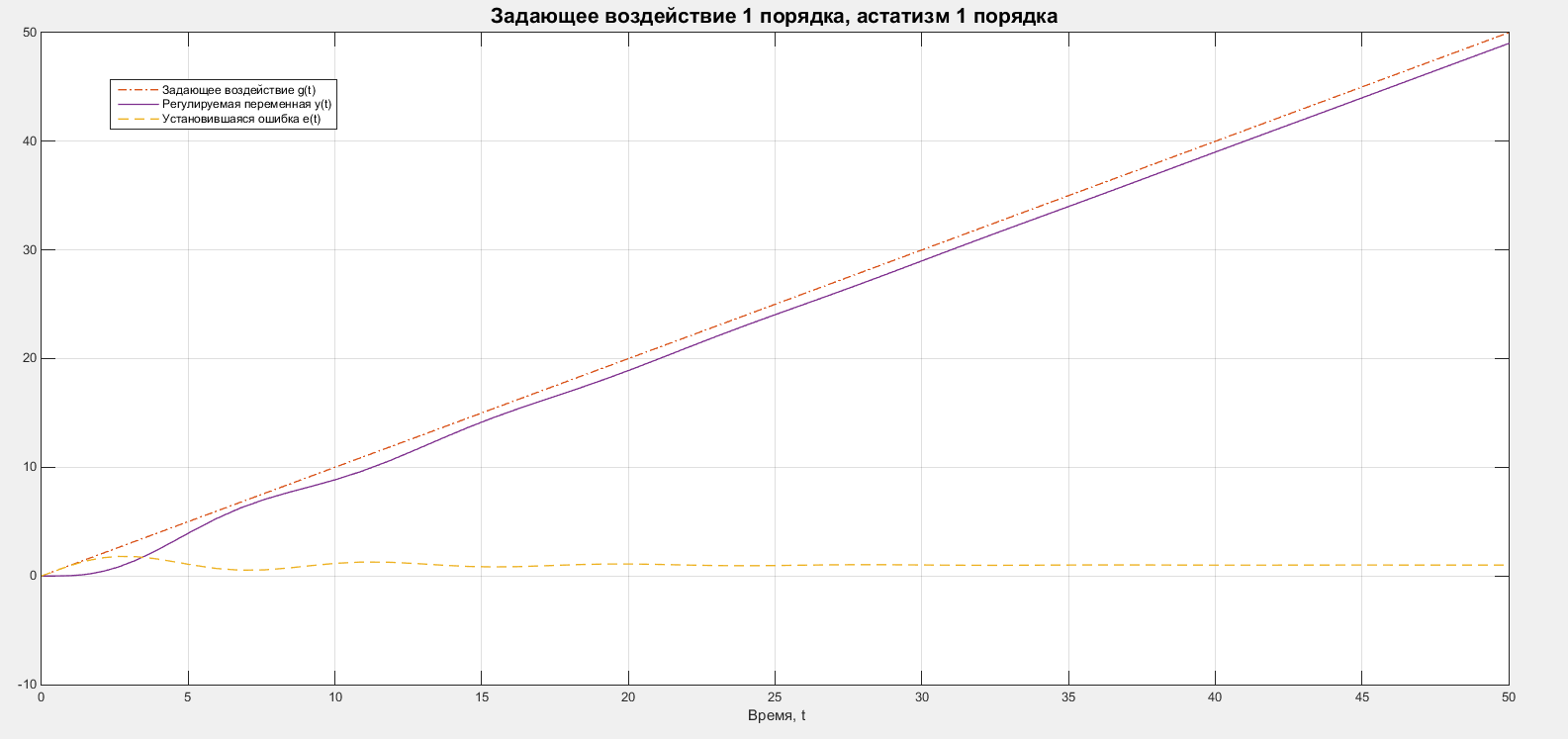
Рисунок 7 – Графики для системы с 1 порядком астатизма и воздействия 1 порядка

Рассмотрим случай задающего воздействия 2 порядка. В качестве задающего воздействия будем рассматривать квадратичную функцию: . Графики задающего воздействия, регулируемой переменной и ошибки представлены на рисунке 8.

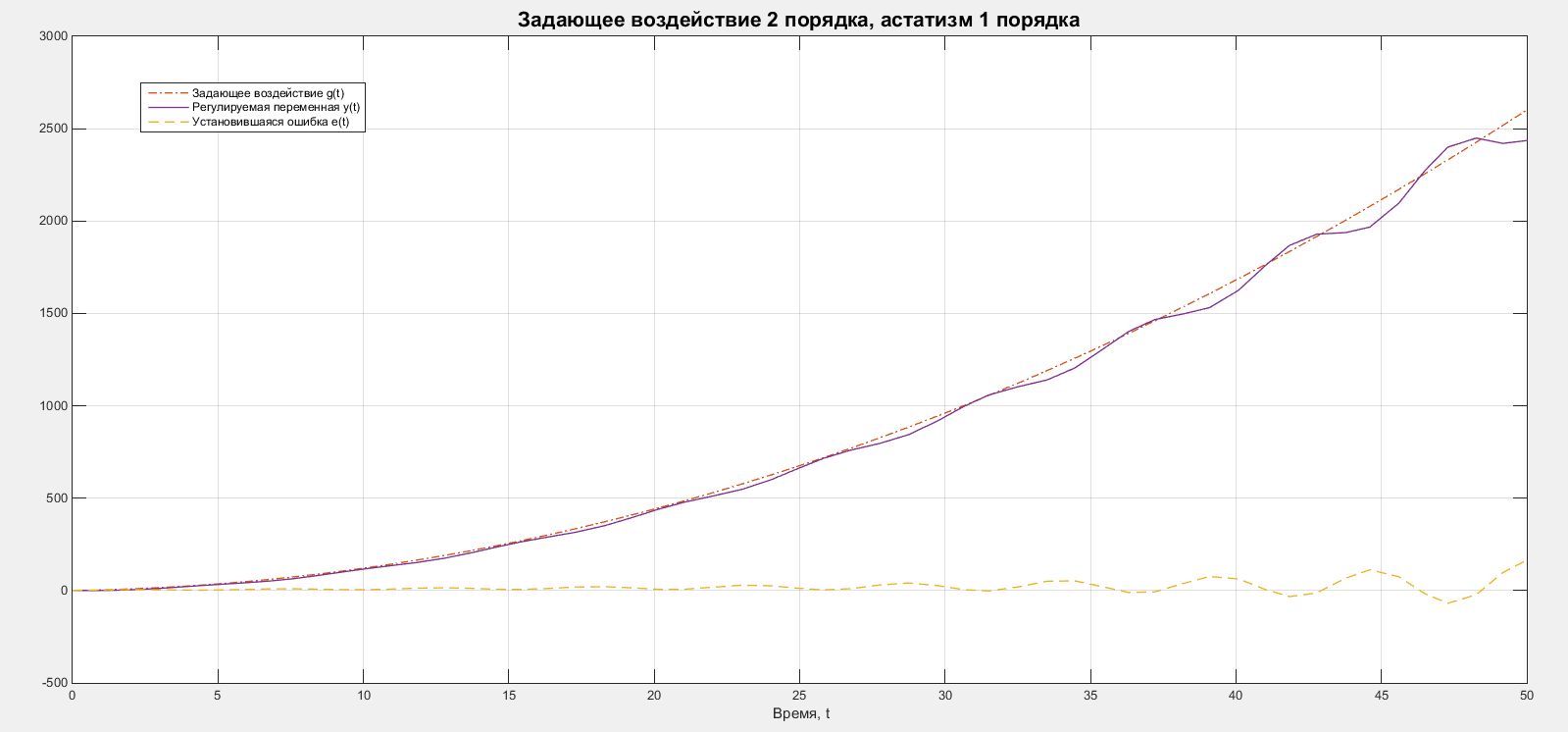
Рисунок 8 – Графики для системы с 1 порядком астатизма и воздействия 2 порядка.

4. Исследование САУ со вторым порядком астатизма

Соберем схему системы с первым порядком астатизма. Схема представлена на рисунке 9.

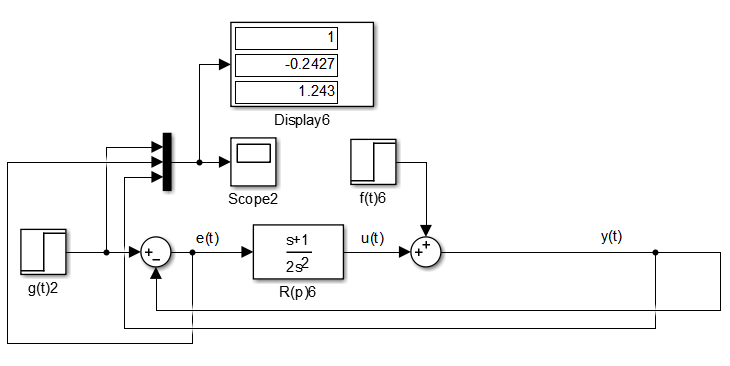Рисунок 9 – Структурная схема системы с астатизмом 2 порядка

Рассмотрим случай задающего воздействия 0 порядка. В качестве задающего воздействия будем рассматривать единичное ступенчатое воздействие c временем запаздывания в 1 секунду: . Графики задающего воздействия, регулируемой переменной и ошибки представлены на рисунке 10.

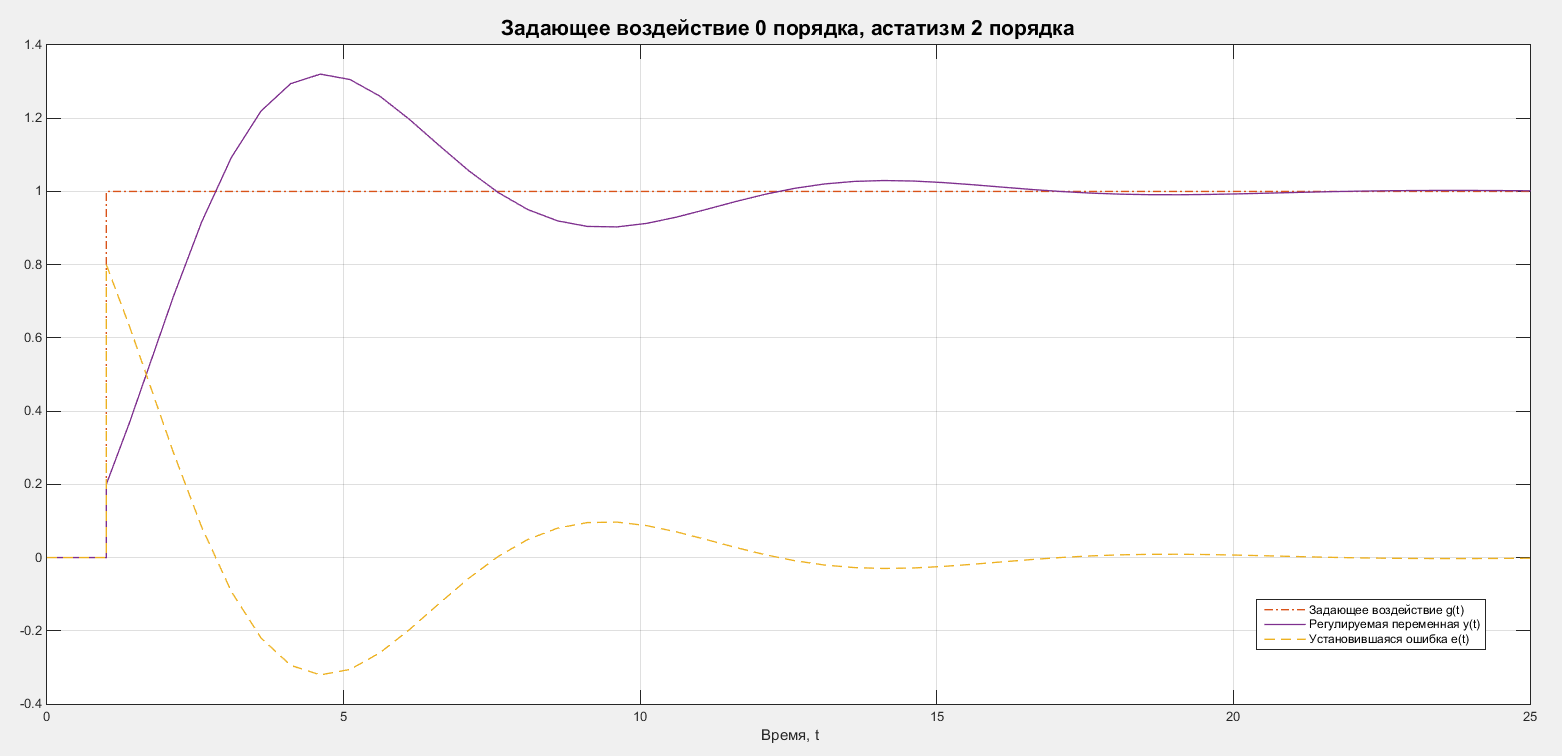
Рисунок 10 – Графики для системы со 2 порядком астатизма и воздействия 0 порядка.

Рассмотрим случай задающего воздействия 1 порядка. В качестве задающего воздействия будем рассматривать функцию единичного наклона: . Графики задающего воздействия, регулируемой переменной и ошибки представлены на рисунке 11.

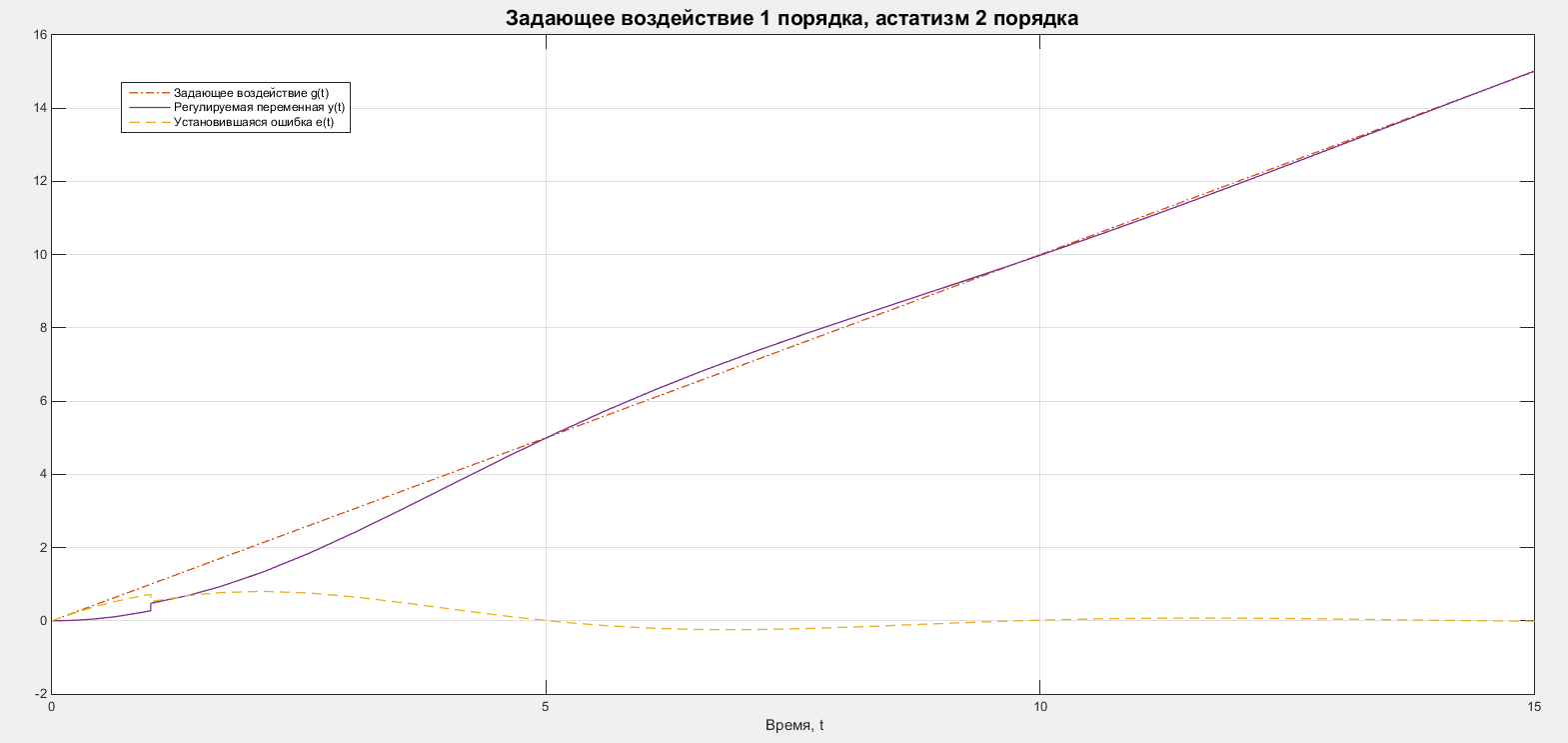
Рисунок 11 – Графики для системы со 2 порядком астатизма и воздействия 1 порядка

Рассмотрим случай задающего воздействия 2 порядка. В качестве задающего воздействия будем рассматривать квадратичную функцию: . Графики задающего воздействия, регулируемой переменной и ошибки представлены на рисунке 12.

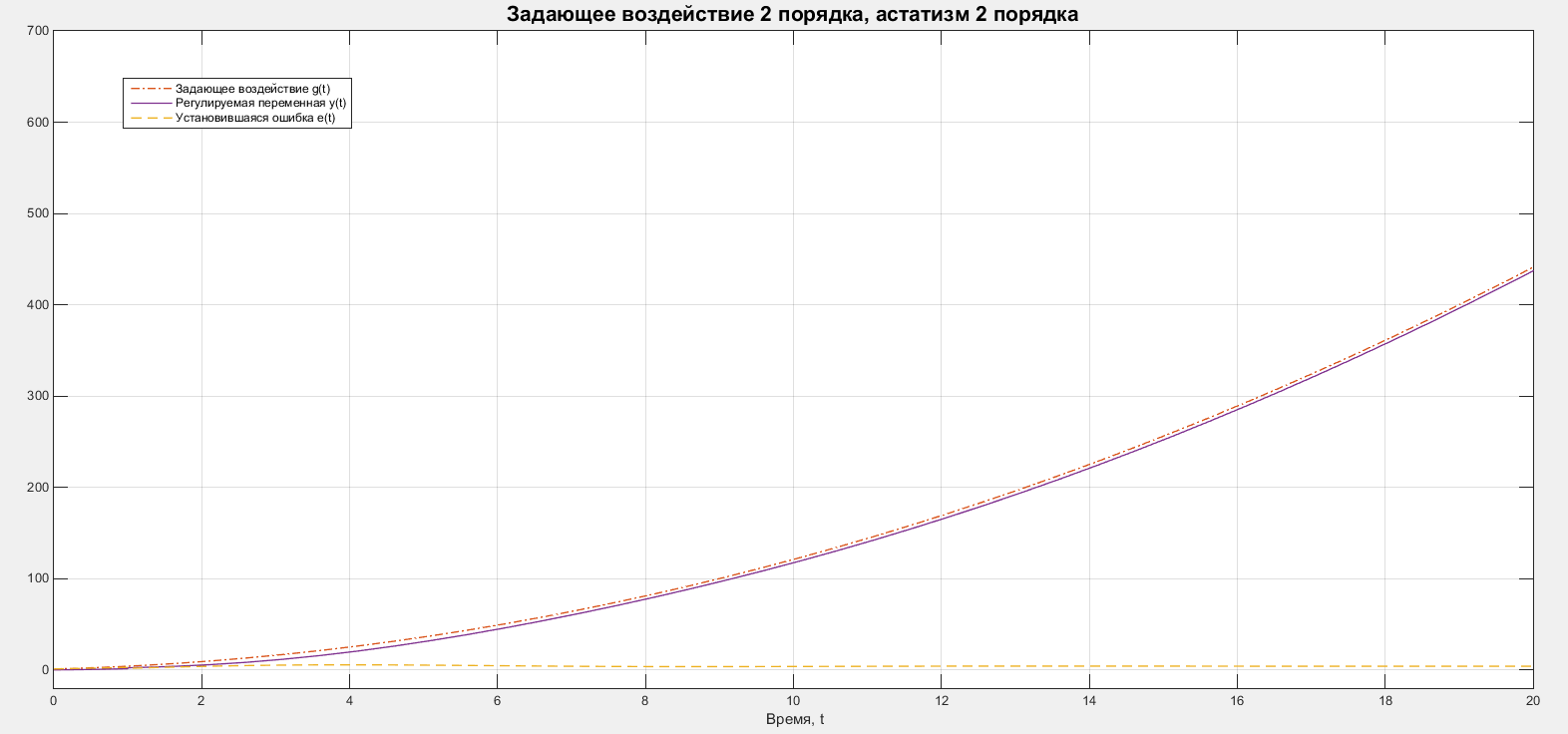
Рисунок 12 – Графики для системы со 2 порядком астатизма и воздействия 2 порядка.

Вывод

В данной лабораторной работе были исследованы САУ с разным порядком астатизма в среде Simulink. Были исследованы системы с 0 – 2 порядками астатизма при воздействиях 0 – 2 порядка. Также были построены графики задающих воздействий, регулируемых переменных и установившейся ошибки. Полученные результаты подтверждают теоретические сведения: если порядок астатизма системы равен порядку задающего воздействия, то ошибка постоянна, если порядок астатизма системы больше порядка задающего воздействия, то ошибка нулевая, если порядок астатизма системы меньше порядка задающего воздействия, то ошибка стремится к бесконечности.