Лаба 2 / Лабораторная работа №2_Токарев_0421_ТОЭ

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

отчет

по лабораторной работе №2

по дисциплине «Теоретические основы электротехники»

Тема: «Исследование линейных резистивных цепей»

Студент гр. 0421		Токарев А.А.
Преподаватель		Яшкардин Р.В.

Санкт-Петербург

2022

Обработка измерений:

2.2.1. Исследование цепи при питании её от двух источников:

Таблица 2.1.

U, В	U1, В	U2, В	U3, В	U4, В	I, мА	I1, мА	I2, мА	I3, мА	I4, мА
1,99	0,34	0,4	1,64	2,04	0,99	0,23	0,27	0,51	0,71

Проверим полученные результаты, используя законы Кирхгофа:

Исходная схема:

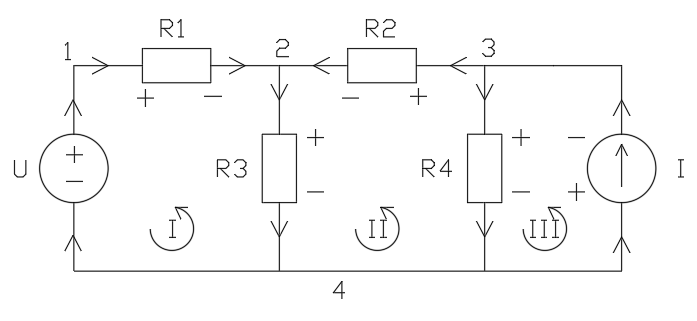
Составим уравнения по I закону Кирхгофа:

Для узла 1: I₁ - I_U = 0

Для узла 2: I₂ + I₁ - I₃ = 0

Для узла 3: -I + I₄ + I₂ = 0

Для узла 4: I_U – I₃ – I₄ + I = 0

Составим уравнения по II закону Кирхгофа:

Для I контура: U – U₃ - U₁ = 0

Для II контура: U₂ + U₃ – U₄ = 0

Для III контура: U₄ – U_I = 0

Подставим измеренные нами значения напряжений и токов в уравнения:

Для узла 2: 0,27 + 0,23 - 0,51 = -0,01 ≈ 0

Для узла 3: -0,99 + 0,71 + 0,27 = -0,01 ≈ 0

Для I контура: 1,99 – 1,64 – 0,34 = 0,01 ≈ 0

Для II контура: 0,4 + 1,64 – 2,04 = 0

Таким образом, все напряжения и токи проверены с помощью законов Кирхгофа.

2.2.2. Определение токов цепи методом наложения:

Таблица 2.2.

Включены источники	I1, мА	I2, мА	I3, мА	I4, мА
U	0,59	0,25	0,33	0,24
I	0,36	0,53	0,16	0,45
U, I	0,23	0,28	0,49	0,69

С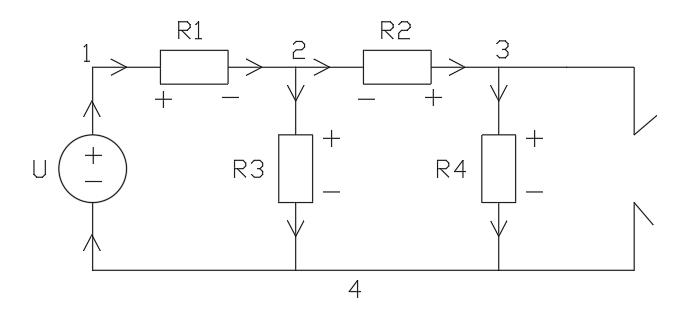 хема при подключенном источнике напряжения:

Схема при подключенном источнике тока:

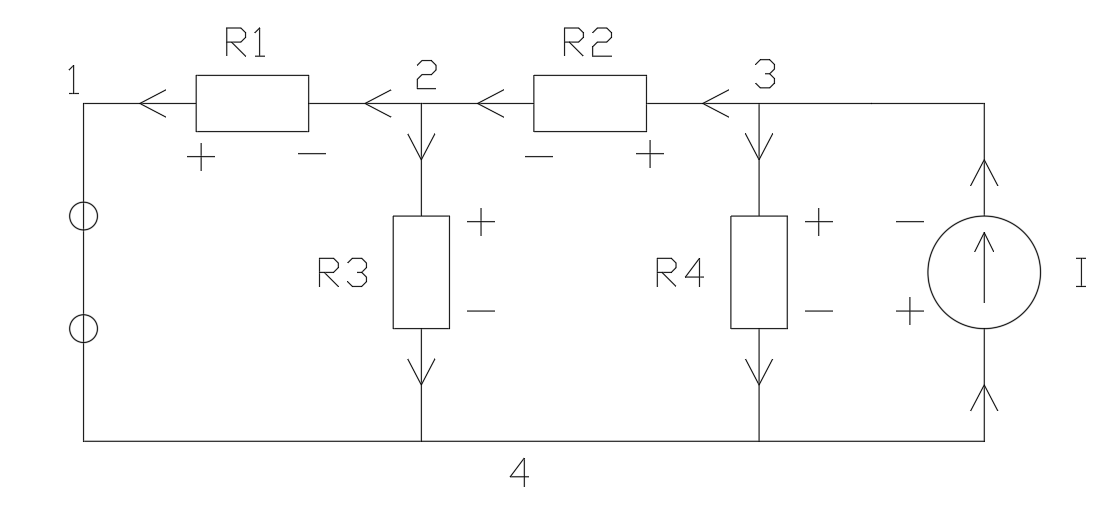
Найдем токи по методу наложения:

I₁ = I₁`- I₁`` = 0,59 – 0,36 = 0,23 [мА]

I₂ = -I₂` + I₂`` = 0,53 – 0,25 = 0,28 [мА]

I₃ = I₃` + I₃`` = 0,33 + 0,16 = 0,49 [мА]

I₄ = I₄` + I₄`` = 0,24 + 0,45 = 0,69 [мА]

Токи, полученные методом наложения, получились приблизительно равными токам, измеренным в пункте 2.2.1.

2.2.3. Определение тока в ветви с сопротивлением R₃ методом эквивалентного источника напряжения:

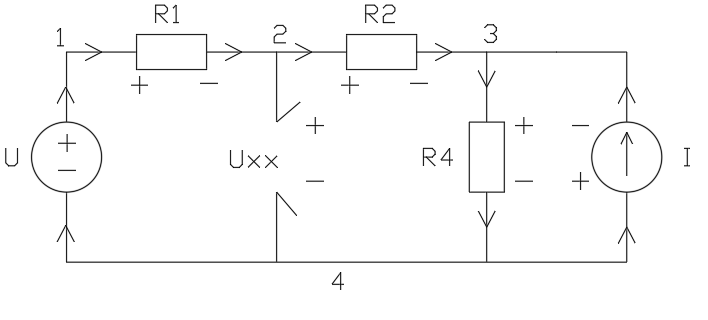U_хх = 2,18 [В]

Найдем R_экв при отключенных источниках питания относительно R₃:

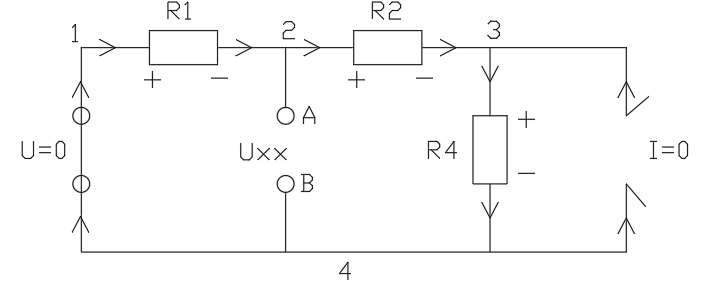
Преобразуем схему: 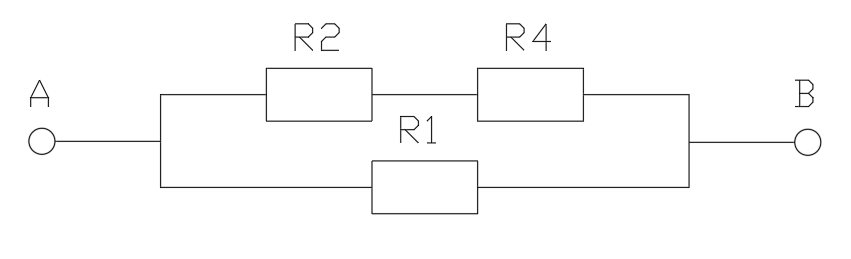Найдем R_экв:

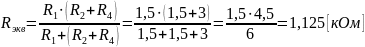
Найдем напряжение U₃ и ток I₃:

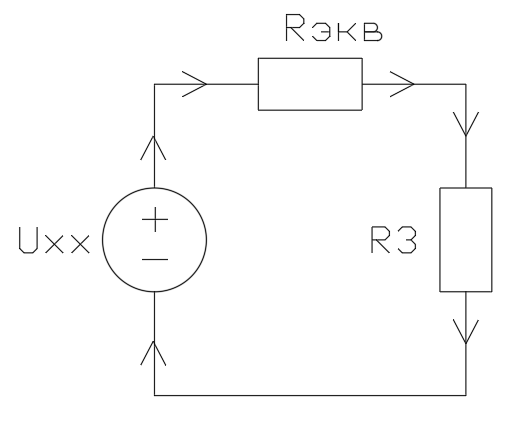
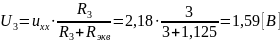
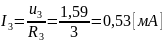
Измеренное значение I₃ = 0,5 [мА]

Таким образом, расчетное значение i₃ получилось приблизительно равно экспериментальному.

2.2.4. Экспериментальная проверка принципа взаимности:

Схема 1:

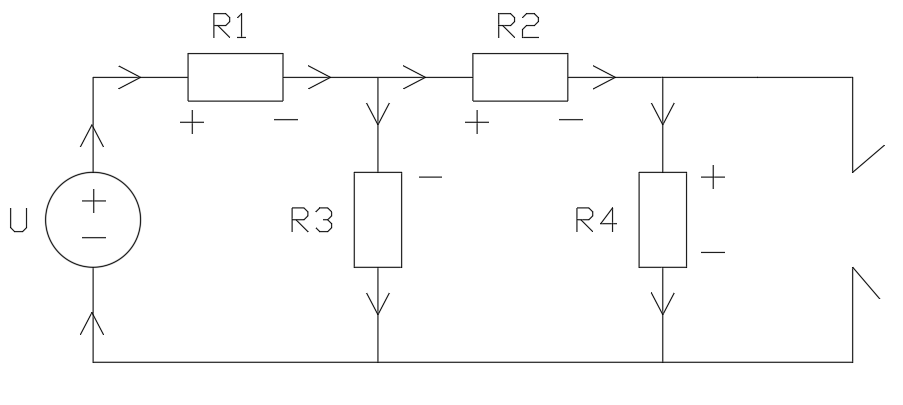
I₃ = 0,34 Схема 2:

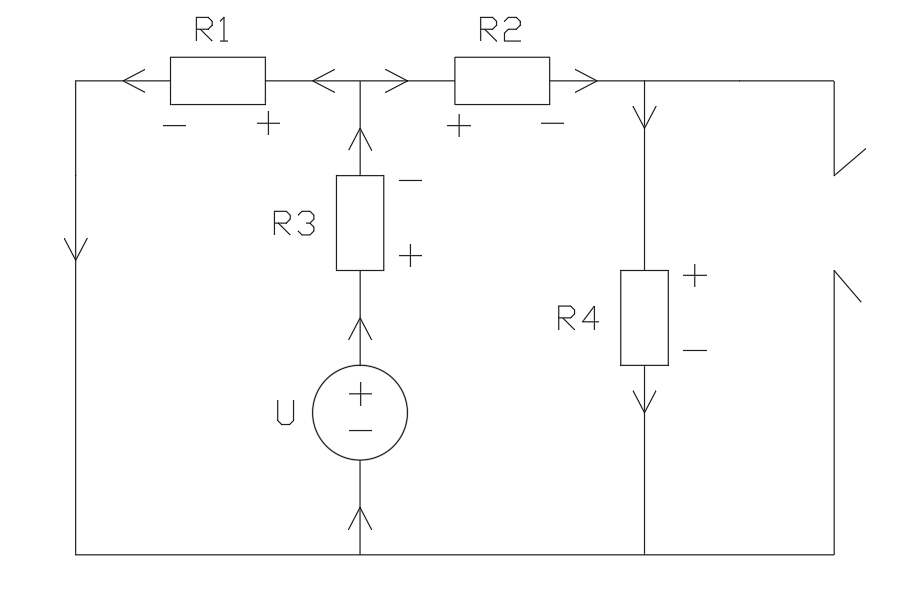I₁ = 0,38 I₃ ≈ I₁, следовательно принцип взаимности выполняется.

Вывод:

В данной лабораторной работе были исследованы линейные разветвленные резистивные цепи с использованием законов Кирхгофа, методов наложения, эквивалентного источника и принципа взаимности. Полученные экспериментальные значения подтверждают теоретически рассчитанные значения.

Ответы на вопросы:

1. Каковы результаты контроля данных в пункте 2.2.1? Ответ: В пункте 2.2.1 проверка экспериментальных данных проводится с помощью уравнений Кирхгофа. Результаты расчета совпадают с экспериментально полученными данными.

2. Изменятся ли токи ветвей, если одновременно изменить полярность напряжения ИН и направление тока ИТ на противоположные? Ответ: Значение токов ветвей не изменится, изменится только направление протекания токов.

3. Чему равно напряжение между узлами «С» и «D» цепи? Ответ: U_CD = U₁ – U₂ = 0,34 – 0,4 = -0,06 [B].

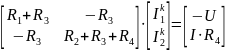
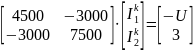
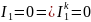
4. Как изменить напряжение ИН, чтобы ток I₁ стал равен нулю? Ответ: Уравнения по ЗТК и ЗНК с учетом того, что I₁ = 0 и U₁ = I₁R₁ = 0: I₁ = 0; I₂ = I₃; U = U₃; Найдем U₃ с помощью метода контурных токов: 1. Преобразуем схему: 2.Составим уравнения: 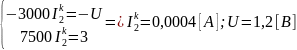Следовательно, надо понизить напряжение до 1,2 В.

5. Почему рис. 2.4, б при U = U₀ реализует схему метода эквивалентного источника напряжения (рис. 2.3,а)? Ответ: Потому что: 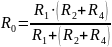=> эти схемы будут одинаковыми:

6. Чему будет равен ток I₁, если ИН поместить в ветвь 4, а ИТ отключить? Ответ:

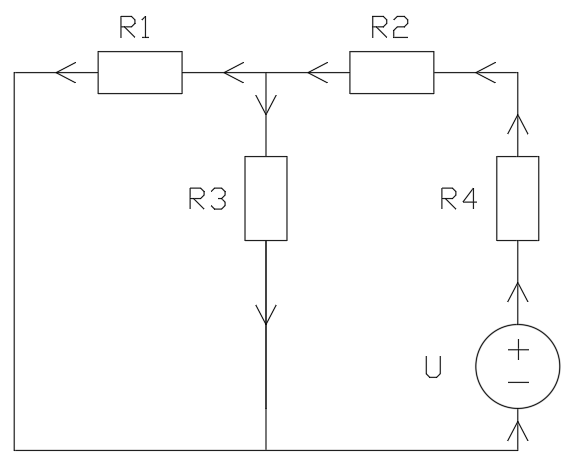
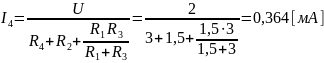
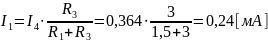
7. Как проконтролировать результаты экспериментов в 2.2.2, 2.2.3 и 2.2.4? Ответ: Проконтролировать можно, сравнив теоретические значения, полученные по разным методам расчета линейных резистивных цепей с экспериментальными значениями, что и было проделано.