Добавил:

allnoobscanswim Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Информационные технологии

Файл:

Лаба 2 / Лабораторная работа №2_Токарев_0421

.docx

Скачиваний:

Добавлен:

26.06.2025

Размер:

119.13 Кб

Скачать

☆

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра Электротехнологической и преобразовательной техники

отчет

по лабораторной работе № 2

по дисциплине «Информационные технологии»

Тема: Переменные и встроенные типы данных

Студент гр. 0421		Токарев А.А.
Преподаватель		Чмиленко Ф.В.

Санкт-Петербург

2021

Цель работы: исследование встроенных типов данных языка С++.

Задания:

Диапазоны целых чисел
Числа с плавающей точкой одинарной точности
Числа с плавающей точкой двойной точности
Представление символов
Определения характеристик общих типов переменных
Определение и инициализация локальных переменных
Область видимости и время жизни переменных

Дополнительные задания:

Демонстрация результата оператора присваивания с потерей точности

Ход работы:

Задание 1.

Проведем с помощью программы datatypes исследование максимальных и минимальных значений, отображения чисел в двоичном и десятичном виде, а также что происходит при превышении максимальных и минимальных значений для целых чисел:

Таблица 1 – Исследование целых чисел

Типы данных	Размер	Диапазон	Число	Двоичный вид
signed char	1 байт	-128...127	12	00001100
			-128	10000000
			128	10000000
unsigned char	1 байт	0…255	12	00001100
			-12	11110100
			244	11110100
			256	00000000
signed short	2 байта	-32768…32767	12	00000000 00001100
			-12	11111111 11110100
			32768	10000000 00000000
			-32768	10000000 00000000
unsigned short	2 байта	0…65535	12	00000000 00001100
			-12	11111111 11110100
			244	11111111 11110100
			65536	00000000 00000000
signed long	4 байта	-2³¹…2³¹ - 1	12	00000000 00000000 00000000 00001100
			2147483647	01111111 11111111 11111111 11111111
			2147483648	10000000 00000000 00000000 00000000
			-2147483648	10000000 00000000 00000000 00000000
unsigned long	4 байта	0…2³² - 1	12	00000000 00000000 00000000 00001100
			4294967295	11111111 11111111 11111111 11111111
			4294967296	00000000 00000000 00000000 00000000
			-1	11111111 11111111 11111111 11111111

Задание 2.

Таблица 2 – исследование вещественных чисел типа float

Типы данных	Размер	Диапазон	Число	Двоичный вид
float	4 байт	1,1810^-38…3,410³⁸	3.40282346638529e+38	01111111 01111111 11111111 11111111
			1.17549435082229e-38	00000000 10000000 00000000 00000000
			1e-46	00000000 00000000 00000000 00000000
			3e+66	01111111 10000000 00000000 00000000
			-3.40282346638529e+38	11111111 01111111 11111111 11111111

Проверим формулу для вычисления значения числа с плавающей точкой для одинарной точности:

(-1)^знак*(1+мантисса/2²³)*2^{(порядок}^{– 127)}

Для числа 4,625 представление в двоичном виде будет выглядеть следующим образом: 01000000 10010100 0000000 0000000

Отсюда мантисса будет равна 2^-3 + 2^-5 = 0,15625, порядок будет равен 129, знак равен 0, следовательно, само число будет равно: (-1)⁰ * (1 + 0,15625) * 2^(129-127) = 1,15625*4 = 4,625

Также исследуем влияние разрядности мантиссы на точность вещественных чисел типа float:

Таблица 3 – исследование влияния разрядности мантиссы на точность вещественных чисел типа float

Типы данных	Размер	Число до преобразования	Число после преобразования	Двоичный вид
float	4 байт	0.2222222222	0.222222223877907	00111110 01100011 10001110 00111001
		555555555555	555555553280	01010011 00000001 01011001 10110001
		1111.1111111	1111.11108398438	01000100 10001010 11100011 10001110
		124567891011	124567887872	01010001 11101000 00000110 10011001
		99.124547874	99.1245498657227	01000010 11000110 00111111 11000101

Как видно из таблицы, максимальное количество значащих цифр для вещественного числа типа float составляет 8 значащих цифр. При превышении этого числа, теряется точность вычислений.

Задание 3.

Таблица 4 – исследование вещественных чисел типа double

Тип данных	Размер	Диапазон	Число	Двоичный вид
double	8 байтов	2,2210^-308…1,7910³⁰⁸	1.79769313486231571e+308	01111111 11101111 11111111 11111111 11111111 11111111 11111111 11111111
			2.22507385850720188e-308	00000000 00010000 00000000 00000000 00000000 00000000 00000000 00000000
			2e-400	00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
			4e+500	01111111 11110000 00000000 00000000 00000000 00000000 00000000 00000000
			4e+600	01111111 11110000 00000000 00000000 00000000 00000000 00000000 00000000

Проверим формулу для вычисления значения числа с плавающей точкой для двойной точности:

(-1)^знак*(1+мантисса/2⁵²)*2^{(порядок}^{– 1023)}

Для числа 3,125 представление в двоичном виде будет выглядеть следующим образом: 01000000 00001001 00000000 0000000 0000000 00000000 00000000 00000000

Отсюда мантисса будет равна 2^-1 + 2^-4 = 0,5625, порядок будет равен 1024, знак равен 0, следовательно, само число будет равно: (-1)⁰ * (1 + 0,5625) * 2^(1024-1023) = 1,5625*2 = 3,125

Также исследуем влияние разрядности мантиссы на точность вещественных чисел типа double:

Таблица 5 – исследование влияния разрядности мантиссы на точность вещественных чисел типа double

Типы данных	Размер	Число до преобразования	Число после преобразования	Двоичный вид
double	8 байтов	0.222222222222222222222	0.22222222222222221	00111111 11001100 01110001 11000111 00011100 01110001 11000111 00011100
		858585858585858585	858585858585858560	01000011 10100111 11010100 10011110 10010100 00101100 01011110 00100100
		1111.11111111111111111111	1111.11111111111109	01000000 10010001 01011100 01110001 11000111 00011100 01110001 11000111
		124567891011121314	124567891011121312	01000011 01111011 10101000 11011101 01100011 11100010 00110011 00001010
		99.1245478741213121484694	99.1245478741213191	01000000 01011000 11000111 11111000 10010111 10100101 10001000 11001011

Как видно из таблицы, максимальное количество значащих цифр для вещественного числа типа double составляет 16 значащих цифр. При превышении этого числа, теряется точность вычислений.

Задание 4.

Проведем с помощью программы datatypes исследование символов в целочисленном виде типа char(символы):

Таблица 6 – исследование символов в целочисленном виде

Типы данных	Размер	Диапазон	Символ	Десятичный вид	Двоичный вид
unsigned char(символы)	1 байт	0…255	я	255	11111111
			h	104	01101000
			2	50	00110010

Задание 5.

Создадим программу, выводящую информацию об основных типах данных. Для этого воспользуемся двумя заголовочными файлами – limits.h для целых чисел и float.h для вещественных чисел:

#include <iostream>

#include <limits.h>

#include <stdio.h>

#include <float.h>

using namespace std;

int main()

{

system("chcp 1251");

system("cls");

cout << "Мин. и макс. значение типа char: "

<< SCHAR_MIN << "\t" << SCHAR_MAX << endl;

cout << "Мин. и макс. значение типа unsigned char: "

<< "0" << "\t" << UCHAR_MAX << endl;

cout << "Мин. и макс. значение типа int: "

<< INT_MIN << "\t" << INT_MAX << endl;

cout << "Мин. и макс. значение типа unsigned int: "

<< "0" << "\t" << UINT_MAX << endl;

cout << "Мин. и макс. значение типа long int: "

<< LONG_MIN << "\t" << LONG_MAX << endl;

cout << "Мин. и макс. значение типа unsigned long int:"

<< "0" << "\t" << ULONG_MAX << endl;

cout << "Мин. и макс. значение типа float: "

<< FLT_MIN << "\t" << FLT_MAX << endl;

cout << "Мин. и макс. значение типа double: "

<< DBL_MIN << "\t" << DBL_MAX << endl;

system("pause");

return 0;

}

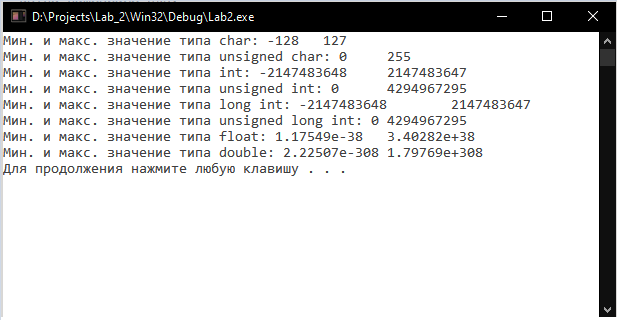
Рисунок 1 – Результаты работы программы по выводу информации об основных типах данных

Задание 6.

Разработаем программу, в которой в самом начале тела функции main объявим переменные различных типов, инициализируем их и с помощью оператора sizeof() определим размер внутреннего представления в байтах для созданных переменных:

#include <iostream>

#include <stdio.h>

using namespace std;

int main()

{

system("chcp 1251");

system("cls");

int a = 12;

bool b = 1;

char c = 104;

long d = 41;

float e = 1.123;

double f = 1.1111;

cout << "a = " << a << endl;

cout << "размер переменной a = " << sizeof(a)

<< " байт(а)" << endl;

cout << "b = " << b << endl;

cout << "размер переменной b = " << sizeof(b)

<< " байт(а)" << endl;

cout << "c = " << c << endl;

cout << "размер переменной c = " << sizeof(c)

<< " байт(а)" << endl;

cout << "d = " << d << endl;

cout << "размер переменной d = " << sizeof(d)

<< " байт(а)" << endl;

cout << "e = " << e << endl;

cout << "размер переменной e = " << sizeof(e)

<< " байт(а)" << endl;

cout << "f = " << f << endl;

cout << "размер переменной f = " << sizeof(f)

<< " байт(а)" << endl;

system("pause");

return 0;

}

Рисунок 2 – Результаты работы программы по определению размера внутреннего представления для созданных переменных

Задание 7.

Разработаем программу, в которой с помощью оператора присваивания производятся изменения первоначальных значений переменных в каждом из трех внутренних блоков и между ними. Также в этой программе выводятся переменные после изменения их значений:

#include <iostream>

#include <stdio.h>

using namespace std;

int main()

{

system("chcp 1251");

system("cls");

int a = 1;

float b = 2.2;

long c = 3;

cout << "Значение перед первым внутренним блоком переменной a = "

<< a << endl;

cout << "Значение перед первым внутренним блоком переменной b = "

<< b << endl;

cout << "Значение перед первым внутренним блоком переменной c = "

<< c << endl;

{

int a = 2;

cout << "Значение в первом внутреннем блоке переменной a = "

<< a << endl;

}

a = 3;

b = 3.3;

c = 4;

cout << "Значение перед вторым внутренним блоком переменной a = "

<< a << endl;

cout << "Значение перед вторым внутренним блоком переменной b = "

<< b << endl;

cout << "Значение перед вторым внутренним блоком переменной c = "

<< c << endl;

{

float b = 4.4;

cout << "Значение во втором внутреннем блоке переменной b = "

<< b << endl;

}

a = 4;

b = 5.5;

c = 7;

cout << "Значение перед третьим внутренним блоком переменной a = "

<< a << endl;

cout << "Значение перед третьим внутренним блоком переменной b = "

<< b << endl;

cout << "Значение перед третьим внутренним блоком переменной c = "

<< c << endl;

{

long c = 123;

cout << "Значение в третьем внутреннем блоке переменной c = "

<< c << endl;

}

system("pause");

return 0;

}

Рисунок 3 – Результаты работы программы

Дополнительное задание.

Доработаем разработанную на предыдущем шаге программу так, чтобы она демонстрировала результат оператора присвоения с потерей точности:

#include <iostream>

#include <stdio.h>

using namespace std;

int main()

{

system("chcp 1251");

system("cls");

int a = 1;

double b = 2.2;

long c = 3;

int d;

cout << "Значение перед первым внутренним блоком переменной a = "

<< a << endl;

cout << "Значение перед первым внутренним блоком переменной b = "

<< b << endl;

cout << "Значение перед первым внутренним блоком переменной c = "

<< c << endl;

{

int a = 2;

cout << "Значение в первом внутреннем блоке переменной a = "

<< a << endl;

}

a = 3;

b = 3.3;

c = 4;

cout << "Значение перед вторым внутренним блоком переменной a = "

<< a << endl;

cout << "Значение перед вторым внутренним блоком переменной b = "

<< b << endl;

cout << "Значение перед вторым внутренним блоком переменной c = "

<< c << endl;

{

float b = 4.4;

cout << "Значение во втором внутреннем блоке переменной b = "

<< b << endl;

}

a = 4;

b = 5.5;

c = 7;

cout << "Значение перед третьим внутренним блоком переменной a = "

<< a << endl;

cout << "Значение перед третьим внутренним блоком переменной b = "

<< b << endl;

cout << "Значение перед третьим внутренним блоком переменной c = "

<< c << endl;

{

long c = 123;

cout << "Значение в третьем внутреннем блоке переменной c = "

<< c << endl;

}

d = a + b;

cout << "Сумма переменных a и b без потери точности равна " << a + b << endl;

cout << "Сумма переменных a и b с потерей точности(переменная d = a + b объявлена как int) равна " << d << endl;

system("pause");

return 0;

}

Рисунок 4 – Результат работы программы, с доработками для демонстрации потери точности

Выводы:

В данной лабораторной работе были исследованы встроенные типы данных в языке программирования С++. Были исследованы и установлены максимальные значения, размеры, максимальное количество значащих цифр для таких типов данных, как int, char, unsigned int, unsigned char, long, unsigned long, float и double. Из приведенных таблиц можно сделать вывод, что чем больше тип данных занимает места в памяти компьютера, тем больший диапазон значений он имеет. Таким образом, недостатком типов данных, имеющих малый диапазон значений (int, char) будет то, что в них не поместится большое число. С другой стороны, недостатком типов данных, имеющих большой диапазон значений (double, long, float) будет то, что они занимают в памяти компьютера значительно больше места. Это может быть важно, например, при программировании микроконтроллеров, когда объемы доступной памяти жестко ограничены.

Прежде чем выбрать тип данных, используемый в нашей программе для той или иной переменной, нужно определить, какого типа будет переменная (логическая, текст, число), если это будет число, определить, будет ли оно целым или вещественным. В случае, если это будет целое число, нужно подумать, в каком диапазоне значений оно будет и какой знак будет иметь. В том случае, если это будет вещественное число, нужно определиться с точностью, с которой это число необходимо задавать.

В случае, если несколько переменных имеют одинаковые имена, значение той из них, что задана глобально (например, в начале функции main() ), будет распространяться на всю функцию, кроме внутренних блоков функции, в которых та же самая переменная может быть объявлена и инициализирована еще раз под тем же самым именем. Соответственно, для внутренних блоков значение переменной будет использовано то, которое инициализировано внутри этого блока, даже если имя этой переменной совпадает с заданной глобально.