Лаба 12 / Лабораторная работа №12_Токарев_0421

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РАПС

отчет

по лабораторной работе №12

по дисциплине «Информатика»

Тема: Графическое решение уравнений и систем уравнений

Студент гр. 0421		Токарев А.А.
Преподаватель		Морозова Е.В.

Санкт-Петербург

2020

Цель работы.

Ознакомиться с графическими методами решения уравнений и систем уравнений.

Постановка задачи.

Задание 1. Решить графически уравнение y = cos²(x) на интервале [0; 1].

Задание 2. Решить графически уравнение х³ – 4х² – 3х + 6 = 0.

Задание 3. Решить графически систему уравнений 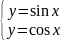в диапазоне х[0; 3] с шагом х = 0,2.

Задание 4. Решить систему уравнений согласно индивидуальному заданию.

Основные теоретические положения.

Кроме аналитического способа решения уравнений f(x) = 0 можно пользоваться и графическим способом. Графический способ наиболее эффективен для решения трансцендентных уравнений. При графическом способе для уравнения строится график y = f(x) и решением уравнения является точка пересечения графика с осью х при у = 0. Если разбить уравнение на две произвольные части, то можно для каждой части построить график. В этом случае решением уравнения будет абсцисса точки пересечения графиков для этих частей. Такой способ может использоваться и для решения систем двух линейных уравнений с двумя неизвестными.

Ход работы.

Задание 1.

- Решить графически уравнение y=cos²(x) на интервале [0;1] значит найти все значения х внутри данного интервала, где функция у пересекает ось Х. Проведем табуляцию значений Х и Y:

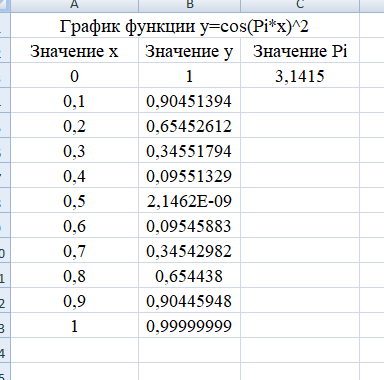
-Построим график функции y=cos²(x):

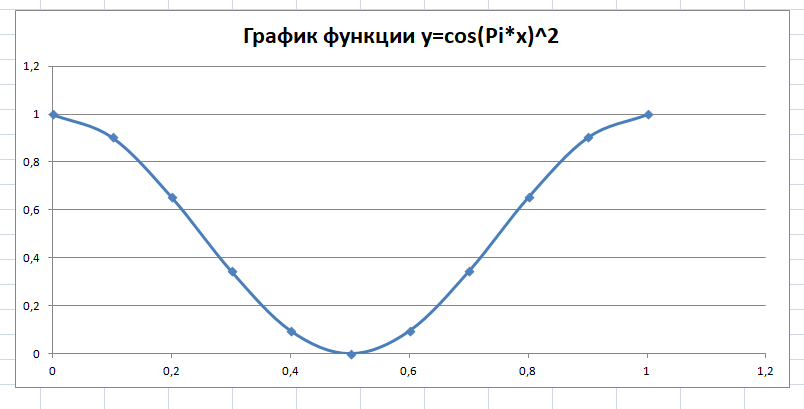
-Из графика видно, что он пересекает ось Х в точке х=0,5, где значение у будет приблизительно равно нулю

Результат работы.

Был графически решено уравнение y=cos²(x)

Задание 2.

-Найдем графическое решение уравнения х³-4х²-3х+6=0. Для этого представим его в виде:

х³ = 4х² + 3х – 6 (2)

и построим на одной диаграмме графики двух функций:

у₁ = х³ левая часть уравнения (2) и

у₂ = 4х² + 3х – 6 правая часть уравнения (2)

-Выполним табуляцию значений х и значений у1 и у2:

-Построим график обеих функций на одном графике:

- Из графиков видно, что на рассмотренном интервале функции у1 и у2 пересекаются только два раза (корни х1 = –1,36 и х2 = 1). Для нахождения третьего корня нужно увеличить диапазон решения. Из графика видно, что при х <–2 функции у1 и у2 расходятся. Значит, решение нужно искать при х>2. Увеличим диапазон до х = 4,8, т. е. х[–2; 4,8]:

-Перестроим графики функций для расширенного диапазона:

-Из графика видно, что третий корень уравнения: х = 4,4 Результат работы.

Было графически решено уравнение х³ – 4х² – 3х + 6 = 0.

Задание 3.

Для нахождения корней уравнений системы

в диапазоне х[0; 3] с шагом х = 0,2, следует выполнить следующие действия:

- Проведем табуляцию значений х и у для обеих функций:

-Построим графики обеих функций:

- Из графиков видно, что общей точкой обеих функций является точка со значениями х = 0.8, у = 0,697

Результат работы.

Графически решена система уравнений

Задание 4.

Решим графически систему уравнений 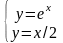х0,2;3, x=0,1

- Проведем табуляцию значений х и у для обеих функций:

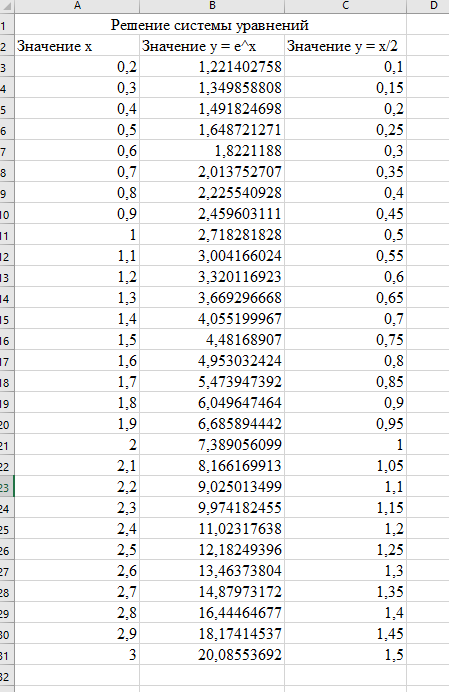
-Построим графики обеих функций:

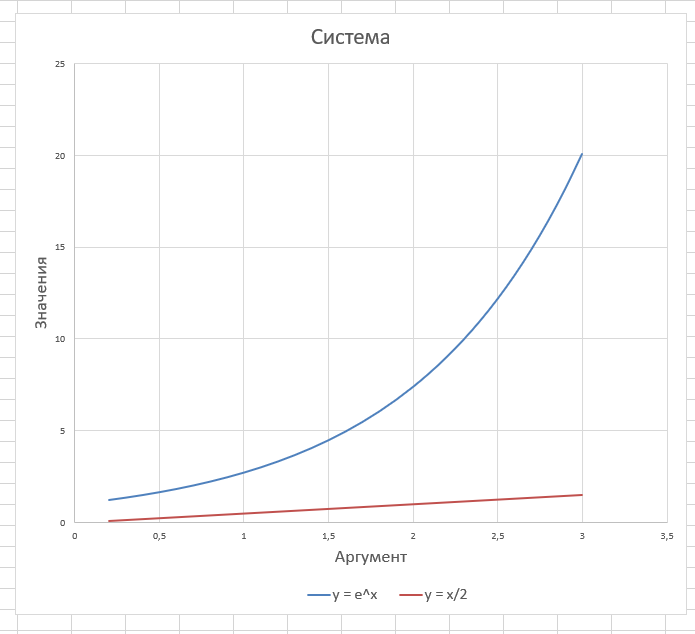-Как можно видеть из графика, система на отрезке [0,2;3] не имеет действительных решений.

Результат работы.

Графически решена система уравнений

Вывод.

Мы ознакомились с графическими методами решения уравнений и систем уравнений в MS Excel.