Лаба 5 / Лабораторная работа №5_Токарев_0421

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РАПС

отчет

по лабораторной работе №5

по дисциплине «Информатика»

Тема: Решение дифференциальных уравнений

Студент гр. 0421		Токарев А.А.
Преподаватель		Морозова Е.В.

Санкт-Петербург

2020

Цель работы.

Освоить базовые принципы решения дифференциальных уравнений в математическом пакете MathCad.

П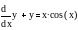 остановка задачи.

Найти функцию у(х), удовлетворяющую дифференциальному уравнению

и имеющую значение 0 при x = 0.

Ход работы.

- Открываем MathCad

- Зададим начальное значение функции как элемент вектора у:

- Создадим функцию Т(х, у), которая вычисляет значение производной при задан­ных значениях независимой переменной и неизвестной функции:

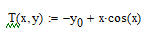
-Определим начальное (точка 0) и конечное значение отрезка интегрирования:

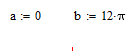
- Укажем число шагов интегрирования:

- Вычислим численное решение уравнения при помощи функции rkfixed:

- Результат вычислений – матрица Z с двумя столбцами, первый из которых содержит значения независимой переменной, а второй — соответствующие зна­чения функции:

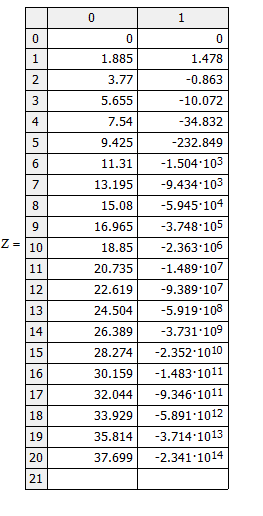
-Построим график полученного решения:

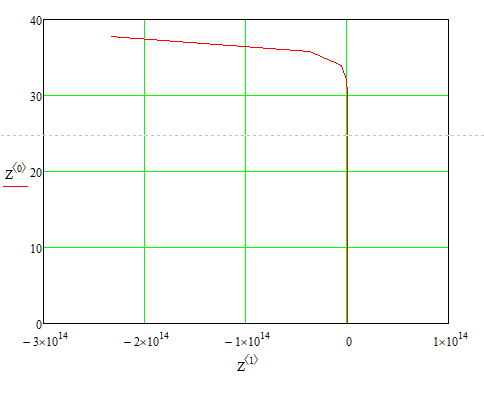
-Увеличим число шагов интегрирования до 100. При этом размерность матрицы Z пропорционально увеличится, а график полученных решений станет более гладким:

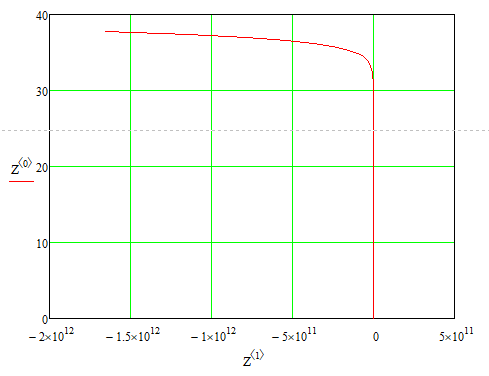
-Если уменьшить число шагов интегрирования до 10, матрица Z станет меньше, а график решений станет менее гладким:

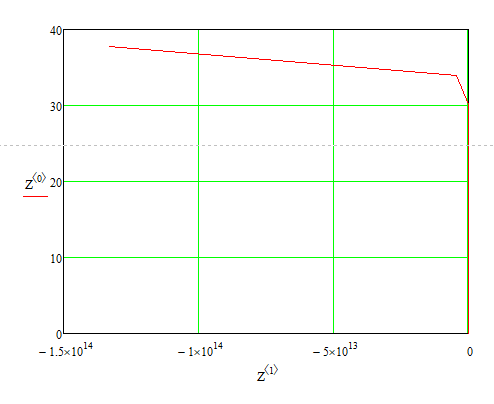
-Таким образом, можно сделать вывод о том, что при увеличении шагов интегрирования в решении дифференциальных уравнений, растет точность решения.

Результат работы.

Б ыло решено дифференциальное уравнение

с помощью функции rkfixed, построен график его решения, исследована зависимость гладкости графика от количества шагов интегрирования.

Вывод.

Мы научились базовым принципам решения дифференциальных уравнений в математическом пакете MathCad.