Лаба 1 / Лабораторная работа №1_Токарев_0421

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РАПС

отчет

по лабораторной работе №1

по дисциплине «Информатика»

Тема: Простые вычисления

Студент гр. 0421		Токарев А.А.
Преподаватель		Морозова Е.В.

Санкт-Петербург

2020

Цель работы.

Освоить базовые принципы простых вычисления в математическом пакете MathCad

Постановка задачи.

Найти ребро куба, равновеликого шару, площадь поверхности которого равна площади боковой поверхности прямого кругового конуса, у которого высота вдвое меньше, чем длина образующей. Объем этого конуса равен 1.

Основные теоретические положения.

Основные геометрические формулы, используемые при расчете:

Объем конуса:

Vk = (1/3)∙ π∙r²∙h

Площадь боковой поверхности конуса:

S = π∙r∙l

Соотношение в конусе между радиусом основания, высотой и длиной образующей:

r² + h² = l²

Площадь поверхности шара:

S = 4∙π∙R²

Объем шара:

Vsh = (4/3)∙π∙R³

Объем куба:

Vkub = a³

Ход работы.

- Открываем MathCad

- Обозначим объем конуса как Vk и присвоим ему значение 1:

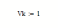
- Введем формулу для расчета радиуса основания конуса:

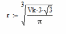
- Введем формулы для вычисления длины образующей и площади боковой поверхности конуса:

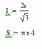
-Введем формулы для расчета радиуса и объема шара:

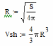
-Введем заключительную формулу:

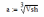
-Наберем имя переменной а и нажмем на знак «=». Таким образом, мы получим значение переменной а:

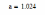
- Поменяем значение переменной Vk на 8 и посмотрим, как поменялось значение переменной а:

Результат работы.

Было рассчитано ребро куба, равновеликого шару, площадь поверхности которого равна площади боковой поверхности прямого кругового конуса, у которого высота вдвое меньше, чем длина образующей.

Вывод.

Мы научились основным принципам базовых вычислений в MathCad