2023-11-29 РЭС подготовка к КР3 Графоаналитический расчет режима покоя VT

Практические занятия по дисциплине «Расчет электронных схем» для подготовки к контрольной работе №3 на тему:

Графоаналитический расчет режима покоя усилительных каскадов с общим эмиттером

(Графоаналитический расчет нелинейных цепей постоянного тока с трёхполюсными нелинейными элементами – биполярными транзисторами)

Версия от 29.11.2023

Задача 3.

Рассчитать режим покоя усилительного каскада по приведённой ниже схеме:

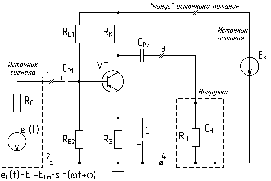
Дано:

R_Б1 = 11 кОм;

R_Б2 = 2 кОм;

R_К = 1 кОм;

R_Э = 200 Ом;

E_К = 12 В;

ВАХ VT – вариант 9.

Найти:

Параметры точки покоя на входных и выходных ВАХ: I_БП; U_БЭП; I_КП; U_КЭП – ?

Решение:

1) Получим схему замещения усилительного каскада по постоянному току. Для этого применим к схеме метод наложения.

Замечание: Метод наложения применим только для расчёта линейных электрических цепей, а схема усилителя является нелинейной. Но, поскольку задача расчёта режима покоя заключается в обеспечении линейного режима работы каскада по переменному току, то, предполагая, что эта задача успешно решена, можно считать схему усилителя условно линейной и применить к ней метод наложения.

Применяя метод наложения для расчёта схемы по постоянному току, необходимо оставить в схеме источник питания E_К , который является источником постоянного напряжения, и исключить из схемы источник входного гармонического сигнала e_Г(t) , который является источником переменного напряжения.

Согласно методу наложения, при исключении источника напряжения его цепь закорачивается, а его внутреннее сопротивление остаётся на месте исключения источника. В результате такого преобразования получаем схему:

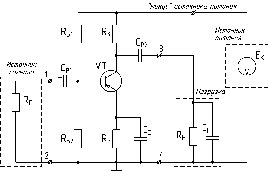
Далее необходимо учесть влияние конденсаторов на схему при постоянном токе. Ток через конденсаторы может протекать только после момента коммутации в течение кратковременного переходного процесса, который заканчивается зарядом конденсаторов до приложенного к ним постоянного напряжения, после этого конденсаторы не пропускают через себя постоянный ток. Поэтому в полученной выше схеме необходимо разомкнуть все конденсаторы, т.к. на постоянном токе они представляют собой бесконечно большое сопротивление. В результате такого преобразования получается схема:

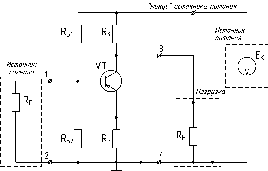
Остаётся удалить из схемы все цепи, которые были последовательно подключены к конденсаторам, в результате получаем схему замещения усилительного каскада по постоянному току:

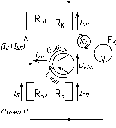
Обозначения всех токов и напряжений в схеме имеют дополнительный индекс "П", что соответствует расчёту этих величин в режиме покоя или, другими словами, в режиме по постоянному току.

Полученная схема замещения соответствует схеме задания положения точки покоя фиксированным напряжением базы с эмиттерной стабилизацией, которую было принято сокращённо называть "Схема Г".

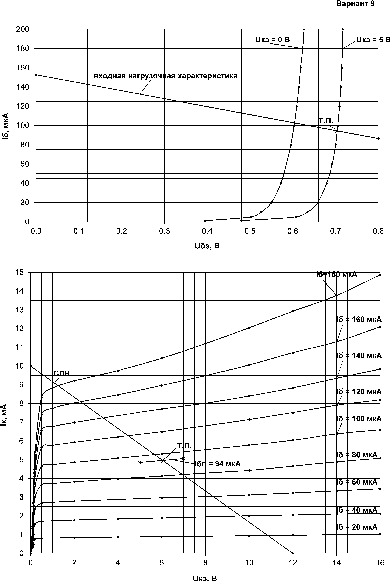
2) Для дальнейшего решения задачи, необходимо построить графики нагрузочных характеристик на семействах входных и выходных ВАХ транзистора. Нагрузочная характеристика, построенная на выходных ВАХ транзистора, имеет своё собственное название – статическая линия нагрузки, сокращённо СЛН.

Графиком СЛН, которую необходимо построить на семействе выходных ВАХ, является уравнение вида U_КЭП = f(I_КП).

Графиком входной нагрузочной характеристики, которую необходимо построить на семействе входных ВАХ, является уравнение вида U_БЭП = f(I_БП).

Получить уравнение входной нагрузочной характеристики U_БЭП = f(I_БП) из второго закона Кирхгоффа в схеме замещения по постоянному току мешает неизвестный ток делителя I_Д , поэтому в схеме требуются дополнительные преобразования.

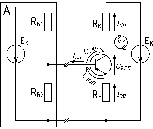
Разделим в схеме источник питания E_К на два одинаковых источника, раздельно питающих входную (R_Б1 и R_Б2) и выходную (R_К и R_Э) цепи схемы. Такое разделение в теории вполне допустимо и соответствует частному случаю теоремы компенсации, но с практической точки зрения подобное разделение достаточно абсурдно, поскольку незачем применять два одинаковых источника питания там, где можно обойтись только одним.

В результате разделения источника получим схему, к которой можно будет применить метод активного двухполюсника для входной цепи:

2.1) Величина ЭДС эквивалентного генератора определяется по схеме активного двухполюсника с разомкнутыми внешними зажимами:

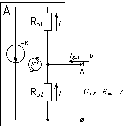
Эквивалентная ЭДС равна напряжению холостого хода на внешних зажимах двухполюсника, она определяется любым методом расчёта линейных цепей постоянного тока.

По закону Ома для участка цепи:

U_Х.Х. = I·R_Б2

По 2ЗК для К1:

E_К = I·(R_Б1 + R_Б2)

Разделив оба полученных уравнения друг на друга, получаем:

U_Х.Х. /E_К = R_Б2 /(R_Б1 + R_Б2) => U_Х.Х. = E_К ·R_Б2 /(R_Б1 + R_Б2) =>

=> E_экв. = E_К ·R_Б2 /(R_Б1 + R_Б2) = 12·2000/(11000+2000) = 1.846 В

2.2) Величина внутреннего сопротивления эквивалентного генератора определяется по схеме активного двухполюсника с разомкнутыми внешними зажимами относительно этих зажимов, при исключении из схемы всех источников питания. Исключая из схемы источник напряжения, его цепь закорачивают.

После преобразований получаем схему:

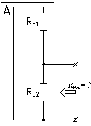
Внутреннее сопротивление эквивалентного генератора соответствует параллельному соединению резисторов R_Б1 и R_Б2 между собой:

R_экв. = R_Б1 //R_Б2 = R_Б1 ·R_Б2 /(R_Б1 + R_Б2) = 11000·2000/(11000+2000) = 1692 Ом

2.3) В результате применения метода активного двухполюсника, входная цепь схемы представляется в виде эквивалентного генератора с E_экв. и R_экв. :

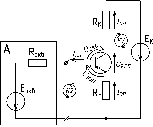
3) Получим уравнение входной нагрузочной характеристики U_БЭП = f(I_БП) из контура 2.

По 2ЗК для К2:

I_ЭП ·R_Э + U_БЭП + I_БП ·R_экв. = E_экв. =>

U_БЭП = E_экв. – I_БП ·R_экв. – I_ЭП ·R_Э

По 1ЗК для VT в АР:

I_ЭП = I_КП + I_БП

Для VT в АР коэффициент передачи тока базы в схеме с общим эмиттером:

β = I_КП /I_БП => I_КП = β·I_БП

Выразим I_ЭП через I_БП и β:

I_ЭП = I_КП + I_БП = β·I_БП + I_БП = I_БП·(β + 1)

Подставляя полученное выражение I_ЭП в формулу U_БЭП , получаем:

U_БЭП = E_экв. – I_БП ·R_экв. – I_БП·(β + 1)·R_Э =>

U_БЭП = E_экв. – I_БП ·[R_экв. + (β + 1)·R_Э] – уравнение входной нагрузочной характеристики, в котором неизвестный коэффициент β надо определить по выходным ВАХ.

4) Получим уравнение U_КЭП = f(I_КП) статической линии нагрузки (СЛН) из контура 3.

По 2ЗК для К3:

I_ЭП ·R_Э + U_КЭП + I_КП ·R_К = E_К =>

U_КЭП = E_К – I_КП ·R_К – I_ЭП ·R_Э

По первому закону Кирхгоффа для транзистора в активном режиме:

I_ЭП = I_КП + I_БП

Для транзистора в активном режиме:

β = I_КП /I_БП => I_БП = I_КП /β

Выразим I_ЭП через I_КП и β:

I_ЭП = I_КП + I_БП = I_КП + I_КП /β = I_КП·(1+ 1/β)

Подставляя полученное выражение I_ЭП в формулу U_КЭП , получаем:

U_КЭП = E_К – I_КП ·R_К – I_КП·(1+ 1/β)·R_Э =>

U_КЭП = E_К – I_КП ·[R_К + (1+ 1/β)·R_Э] – точное уравнение СЛН.

5) Если в точном уравнении СЛН пренебречь величиной 1/ β, считая, что 1/β ≈ 0, то получим приближённое уравнение СЛН:

U_КЭП = E_К – I_КП ·(R_К + R_Э) – приближённое уравнение СЛН.

Это уравнение вида y = k·x+b, является линейной математической зависимостью, где y = U_КЭП ; x = I_КП ; k = –(R_К + R_Э); b = E_К . Графиком такой зависимости является прямая, которая строится по двум точкам. Для простоты рассчитываются точки пересечения прямой с осями, которые находятся при поочерёдном приравнивании к нулю значения функции и аргумента функции.

При I_КП = 0 => U_КЭП = E_К . Учитывая, что горизонтальной осью на графиках ВАХ принято выбирать ось напряжений, получаем точку с координатами (E_К ; 0) = (12 В; 0 мА).

При U_КЭП = 0 => 0 = E_К – I_КП ·(R_К + R_Э) => I_КП = E_К /(R_К + R_Э) = 12 / (1000 + 200) = 10 мА. Учитывая, что вертикальной осью на графиках ВАХ принято выбирать ось токов, получаем точку с координатами (0 В; 10 мА).

По полученным координатам двух точек (12 В; 0 мА) и (0 В; 10 мА), на семействе выходных ВАХ транзистора строится график прямой СЛН.

6) Величина коэффициента β должна определяться в окрестности точки покоя. Поскольку положение точки покоя на выходных ВАХ неизвестно, поэтому определяем среднюю величину β по точкам пересечения СЛН с семейством выходных ВАХ в области активного режима работы транзистора.

Составляется таблица, в которой первые два столбца являются координатами точек пересечения, а третий столбец рассчитывается по этим координатам по формуле β = I_КП /I_БП :

IБП , мкА	IКП , мА	β
20	0.9	45
40	2.0	50
60	3.1	51.7
80	4.2	52.5
100	5.3	53
120	6.3	52.5
140	7.25	51.8
160	8.2	51.3

По данным третьего столбца определяется среднее значение: β_ср. = 51.0 .

7) Используем полученную величину β_ср. для построения графика входной нагрузочной характеристики по уравнению, полученному в пункте 3:

U_БЭП = E_экв. – I_БП ·[R_экв. + (β + 1)·R_Э] – уравнение входной нагрузочной характеристики.

Это уравнение вида y = k·x+b, является линейной математической зависимостью, где y = U_БЭП ; x = I_БП ; k = –[R_экв. + (β + 1)·R_Э]; b = E_экв. . Графиком такой зависимости является прямая, которая строится по двум точкам. Для простоты рассчитываются точки пересечения прямой с осями, которые находятся при поочерёдном приравнивании к нулю значения функции и аргумента функции.

При U_БЭП = 0 => 0 = E_экв. – I_БП ·[R_экв. + (β + 1)·R_Э] => I_БП = E_экв. /[R_экв. + (β + 1)·R_Э] = = 1.846/[1692+(51+1)·200] = 152.7 мкА. Учитывая, что вертикальной осью на графиках ВАХ принято выбирать ось токов, получаем точку с координатами (0 В; 152.7 мкА).

При I_БП = 0 => U_БЭП = E_экв . Учитывая, что горизонтальной осью на графиках ВАХ принято выбирать ось напряжений, получаем точку с координатами (E_экв ; 0) = (1.846 В; 0 мкА). Поскольку эта точка находится за пределами графика входных ВАХ, то необходимо рассчитать другую точку графика прямой, подставляя в уравнение предельное значение с графика ВАХ U_БЭ = 0.8 В.

При U_БЭП = 0.8 В => 0.8 = E_экв. – I_БП ·[R_экв. + (β + 1)·R_Э] => I_БП = (E_экв.– 0.8)/[R_экв. + (β + 1)·R_Э] = = (1.846– 0.8)/[1692+(51+1)·200] = 86.50 мкА, получаем точку с координатами (0.8 В; 86.50 мкА).

По полученным координатам двух точек (0 В; 152.7 мкА) и (0.8 В; 86.50 мкА), на семействе входных ВАХ транзистора строится график прямой входной нагрузочной характеристики.

Входные вольтамперные характеристики транзистора значимо отличаются друг от друга только в режиме насыщения при напряжениях U_КЭ < 0.35 В. В области активного режима при напряжениях U_КЭ > 1 В графики входных ВАХ практически сливаются в одну линию. Поэтому координаты точки покоя определяются по пересечению входной нагрузочной характеристики с входной ВАХ транзистора при U_КЭ = 5 В.

Координаты точки покоя I_БП и U_БЭП , определённые по графикам:

I_БП ≈ 94 мкА;

U_БЭП ≈ 0.705 В.

8) Координаты точки покоя определяются в точке пересечения СЛН с выходной ВАХ при расчётном токе базы покоя I_БП = 94 мкА. Но на семействе выходных ВАХ нет такой характеристики, есть только ближайшие к ней характеристики на 80 мкА и на 100 мкА.

Ток базы ближайшей меньшей характеристики, обозначим как I_Б1 = 80 мкА, а ближайшей большей обозначим как I_Б2 = 100 мкА. Для нахождения положения точки покоя необходимо между характеристиками I_Б1 и I_Б2 достроить небольшой участок характеристики для I_БП в окрестности точки решения. Сначала выбираются две вертикальные вспомогательные линии сетки слева и справа от предполагаемой области решения, в нашем случае, это линии сетки U_КЭ при 5 В и 7 В. Затем измеряется расстояние X в мм, а потом рассчитывается методом пропорции и откладывается расстояние Y в мм, так, как это показано на рисунке.

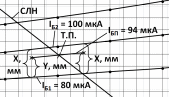
Пропорция составляется следующим образом: расстояние X [мм] соответствует разнице токов базы ΔI_Б  между соседними характеристиками ΔI_Б = I_Б2 – I_Б1 = 20 мкА, а расстояние Y [мм] соответствует разнице между током базы покоя и нижней характеристикой, т.е. I_БП – I_Б1 =  = 94 – 80 = 14 мкА.

Получаем пропорцию:

X, мм — (20 мкА = ΔI_Б = I_Б2 – I_Б1 )

Y, мм — (14 мкА = I_БП – I_Б1 )

Из пропорции определяется Y [мм]:

Y = ( 14 мкА / 20 мкА ) × X, мм.

Если при U_КЭ = 5 В измеренное расстояние X составляет 9.5 мм, то расчётное расстояние Y = 6.65 мм откладывается вверх от нижней характеристики I_Б1 = 80 мкА и отмечается точкой, которая на рисунке обозначена крестиком. Если при U_КЭ = 7 В измеренное расстояние X составляет 10 мм, то вверх от характеристики 80 мкА откладывается расчётное расстояние Y = 7 мм. Полученные точки соединяются прямой линией, которая будет соответствовать участку выходной характеристики при I_БП = 94 мкА.

Из графиков определяются координаты точки покоя по пересечению СЛН с участком характеристики при токе базы покоя:

I_КП ≈ 4.9 мА;

U_КЭП ≈ 6.1 В.

9) Анализируем допустимость пренебрежения величиной 1/β при построении приближённого графика СЛН в пункте 5.

По найденным величинам I_КП и I_БП определяем точное значение β в точке покоя:

β = I_КП /I_БП =4.9·10^–3/(94·10^–6) = 52.1

Строим точный график СЛН по точному значению β, не пренебрегая величиной 1/β.

U_КЭП = E_К – I_КП ·[R_К + (1+ 1/β)·R_Э] – точное уравнение СЛН.

При I_КП = 0 => U_КЭП = E_К , получаем точку с координатами (E_К ; 0) = (12 В; 0 мА).

Следовательно, графики приближённой и точной СЛН пересекают ось напряжений при одинаковых значениях 12 В.

При U_КЭП = 0 => 0 = E_К – I_КП ·[R_К + (1+ 1/β)·R_Э] => I_КП = E_К /[R_К + (1+ 1/β)·R_Э] = = 12/[1000+ (1+ 1/52.1)·200] = 9.968 мА, получаем точку с координатами (0 В;  9.968 мА).

Следовательно, график точной СЛН пересекает ось токов в значении 9.968 мА, а приближённая СЛН пересекает ось токов в значении 10 мА. Погрешность расчёта при пренебрежении величиной 1/β составила:

(10–9.968)/9.968 = +0.32%.

10) Вывод: отклонение в +0.32% несущественное, графики точного и приближённого уравнения СЛН проходят одинаково, т.е. величиной 1/β можно пренебрегать. Дополнительных расчётов для последовательного приближения к более точным результатам не требуется.