Контрольная работа 3

Контрольная работа «квантовое ограничение»

Рассчитайте и постройте график соотношения между шириной одномерной

прямоугольной потенциальной ямы с бесконечной высотой потенциального барьера

и энергией первого разрешенного состояния Е1 в ней, варьируемой в диапазон от

0,05 до 2 эВ для электронов с эффективной массой m*:

• 0,05m₀;

• 0,1m₀;

• 0,15m₀.

Решение:

Энергия квантованных состояний в одномерной потенциальной яме с бесконечными стенками выражается как:

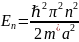
где

En – это энергия n-го состояния,

ℏ – постоянная Дирака,

m∗ – эффективная масса электрона,

a – ширина ямы,

n – номер квантового уровня (для первого состояния n=1).

Поскольку задача требует соотношения между шириной ямы a и энергией первого разрешенного состояния E₁, мы можем переписать выражение для E₁ в виде:

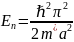
Из этой формулы мы можем выразить a:

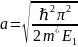
Значение ℏ=1.05×10^-34 Дж·с.

Масса электрона m₀=9.1×10^-31 кг.

E1 в джоулях мы можем получить, перемножив значение в электронвольтах на 1.6×10^-19 Дж/эВ.

Проанализируем значения в диапазоне от 0.05 эВ до 2 эВ при различных эффективных массах m^*.

1. При m^*=0.05m₀.

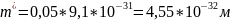
2. При m^*=0.1m₀.

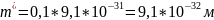
3. При m^*=0.15m₀.

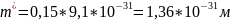
Теперь, с помощью формулы для a, мы рассчитаем ширину ямы для данного диапазона энергий с учетом различной эффективной массы.

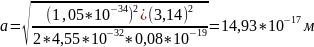
2. Рассчитайте значение ширины одномерной прямоугольной бесконечно глубокой

потенциальной ямы, при котором энергетический зазор между первым и вторым

разрешенными состояниями в ней был равен ΔЕ12:

• 0,05 эВ;

• 0,1 эВ;

• 0,13 эВ.

Эффективная масса электронов m^*=0,06m₀.

Для расчета ширины одномерной прямоугольной потенциальной ямы, рассмотрим энергии первого E₁ и второго E₂ разрешенных состояний. Эти энергии выражаются как:

где:

• En - энергия n-го состояния,

• ℏ - приведенная постоянная Планка, ℏ≈1.05×10^-34 Дж·с,

• m∗ - эффективная масса электрона,

• a - ширина ямы,

• n - номер квантового состояния.

Энергетический зазор между первым и вторым состоянием ΔE₁₂ задается как:

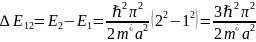
Откуда a можно выразить как:

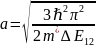
Произведем расчет для различных значений ΔE₁₂ при эффективной массе электронов m^*=0.06m₀. Масса покоя электрона m₀ равна примерно 9,1×10^-31 кг, следовательно:

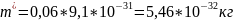
1. При ΔE₁₂=0,05 эВ

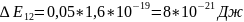
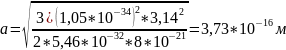
2. При ΔE₁₂=0,1 эВ

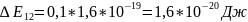
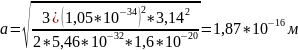
3. При ΔE₁₂=0,13 эВ

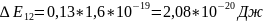
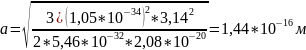
3. Рассчитайте и постройте график зависимости плотности состояний электронов в квантовой плёнке толщиной 20нм от энергии электронов E, отсчитываемой от дна зоны проводимости полупроводника при эффективной массе электрона m^*:

• 0,04m₀;

• 0,07m₀.

Для решения задачи и построения графика плотности состояний D(E) электронов в квантовой плёнке, начнём с определения основных формул и понятий.

Основные формулы

1. Плотность состояний в квантовой плёнке для области дискретных уровней определяется как:

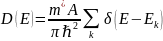
где

A - площадь плёнки,

m^* - эффективная масса электрона,

E_k - энергетические уровни в квантовой плёнке,

ℏ - постоянная Дирака.

δ — дельта-функция Дирака,

E - энергия,

Ek - энергетические уровни в квантовой плёнке,

суммирование ведётся по всем возможным энергетическим уровням k.

2. Энергетические уровни в квантовой плёнке даны формулой:

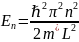
где:

n - квантовое число (принимает значения 1, 2, 3,...),

ℏ - приведённая постоянная Планка,

m^* - эффективная масса электрона,

L - толщина квантовой плёнки.

Расчет m^*:

1. m^*=0,04*9,1*10^-31=3,64*10^-32

2. m^*=0,07*9,1*10^-32=6,38*10^-32

5. Рассчитайте и постройте график зависимости плотности состояний электронов в квантовой точке 20 х 20 х20 нм³ от энергии электронов E, отсчитываемой от дна зоны проводимости полупроводника при эффективной массе электрона m^*:

0,04m₀;

0,07m₀.

Энергетические уровни в квантовой точке для трех измерений можно выразить через формулу:

-
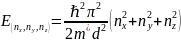