Атомная физика. Строение вещества. 4 Семестр / Zadachi_1 (1)

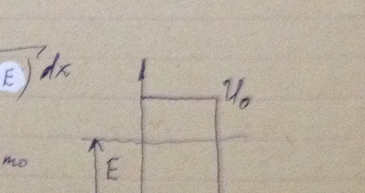
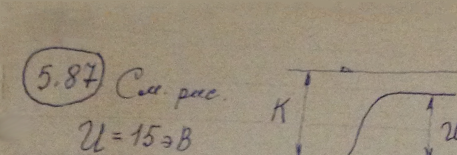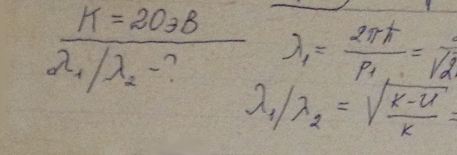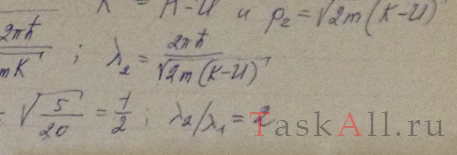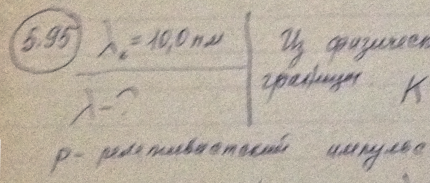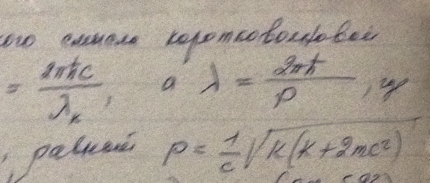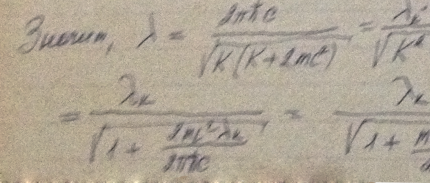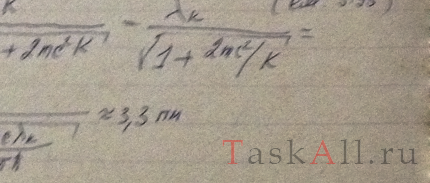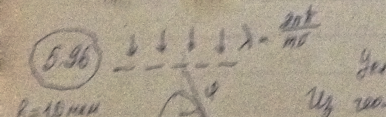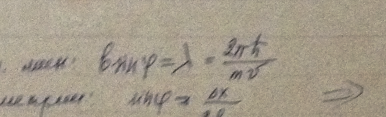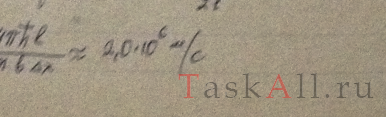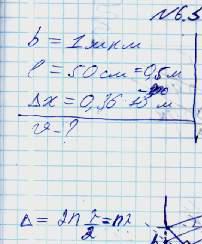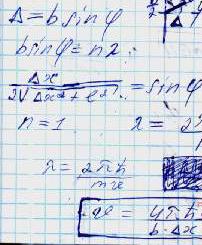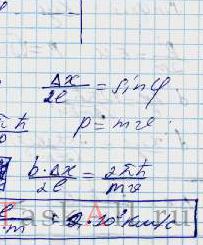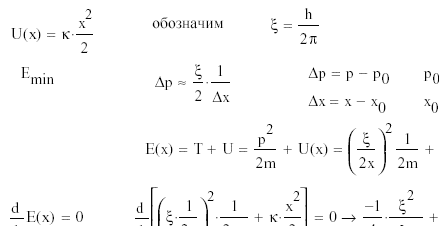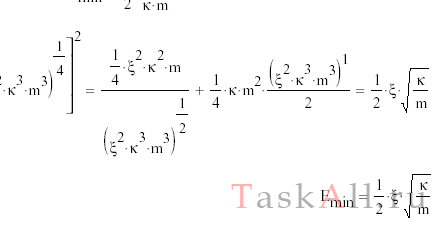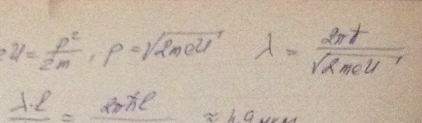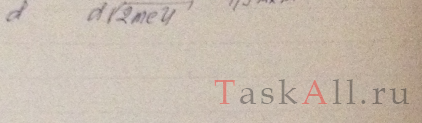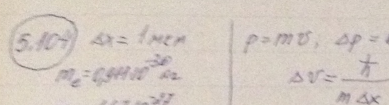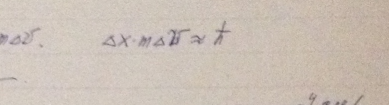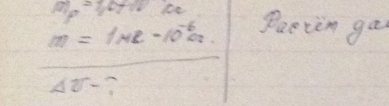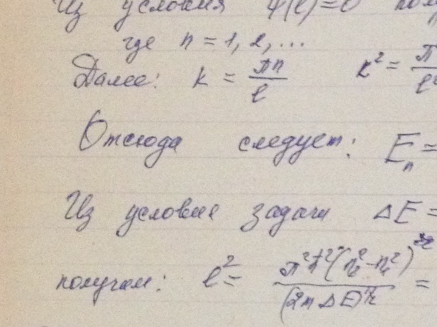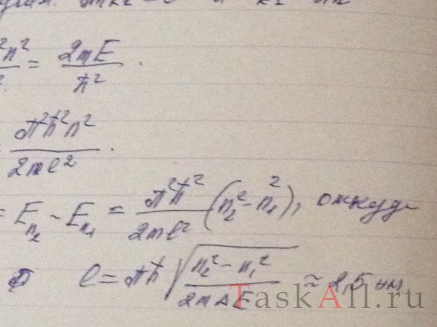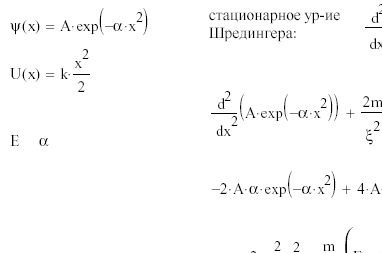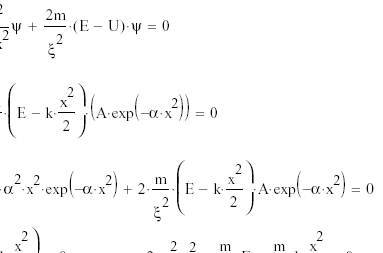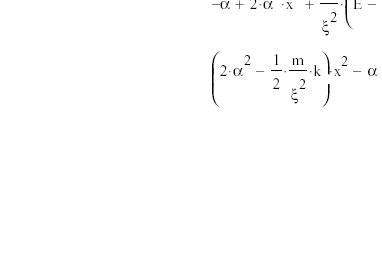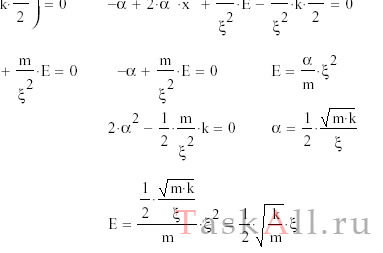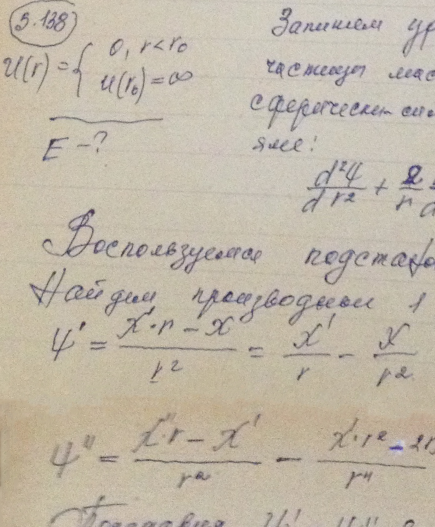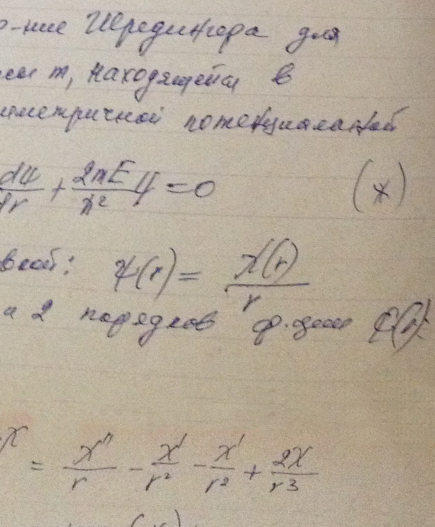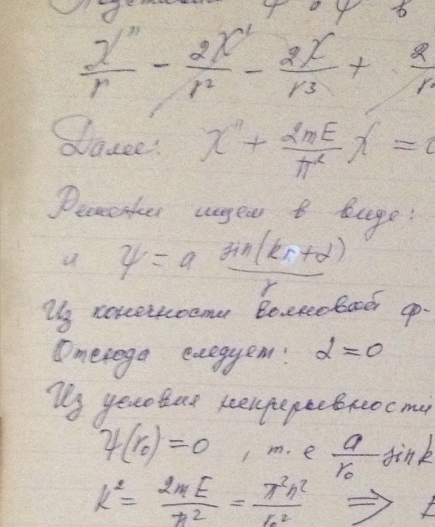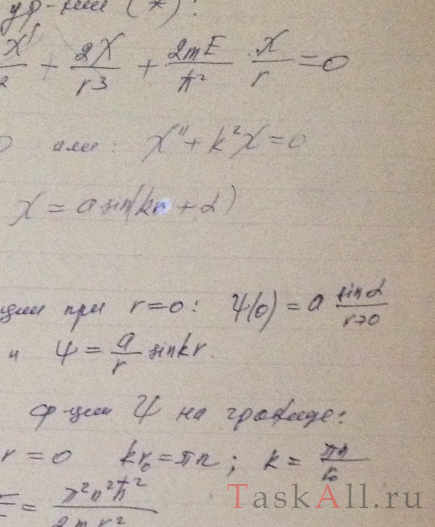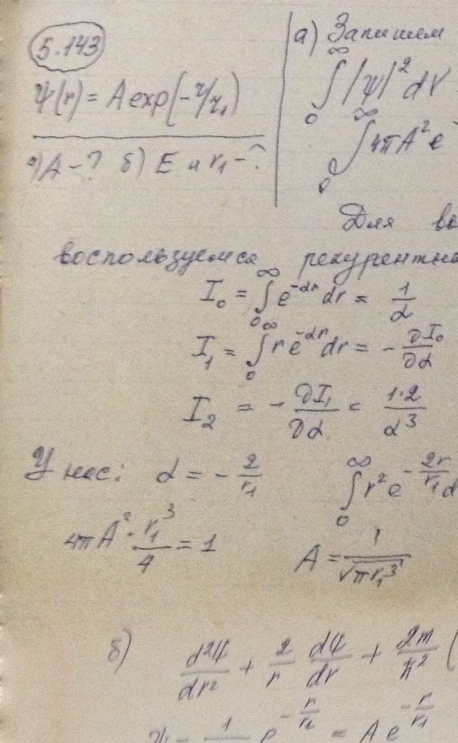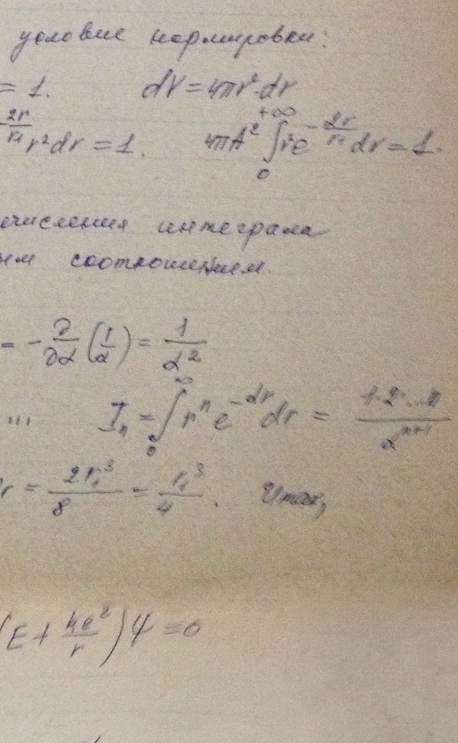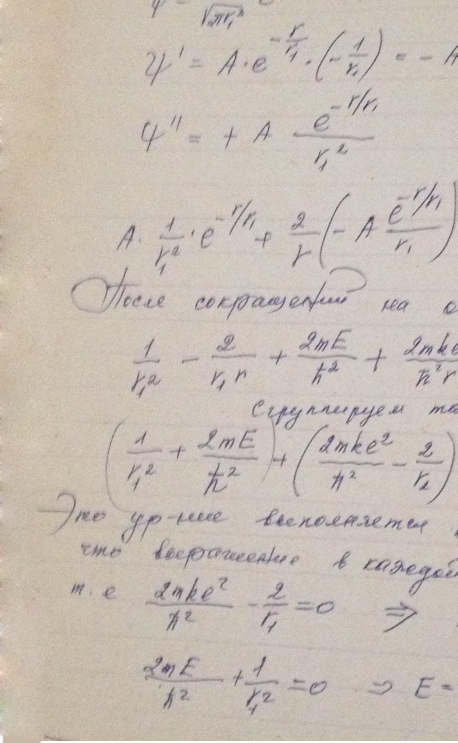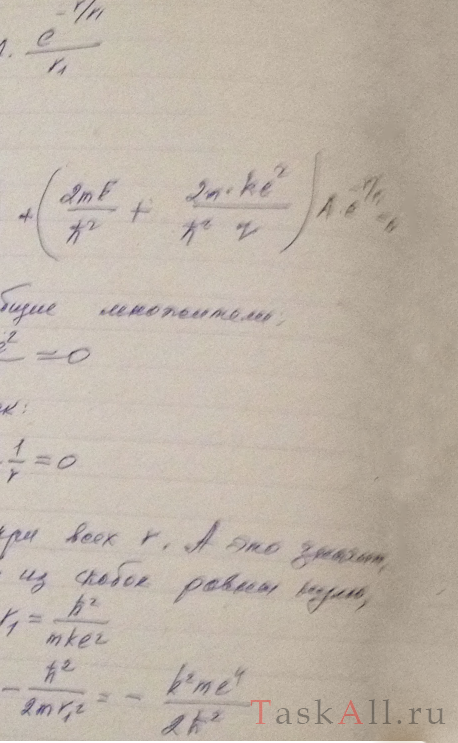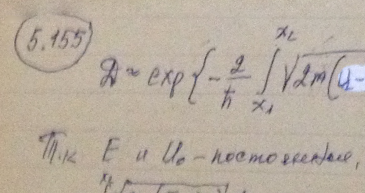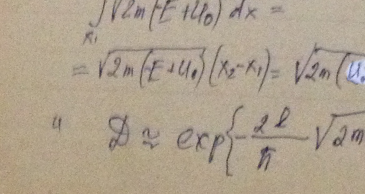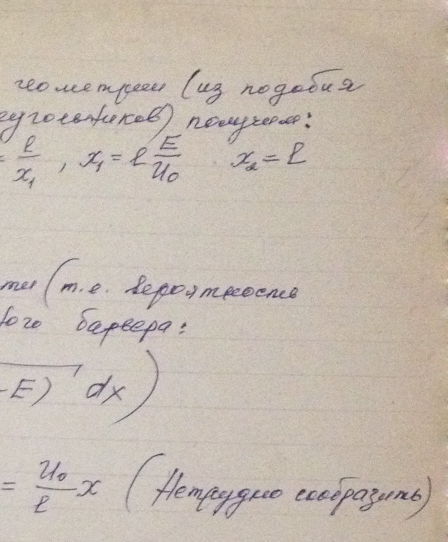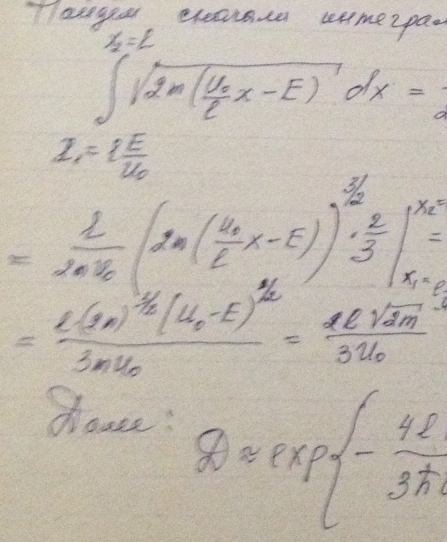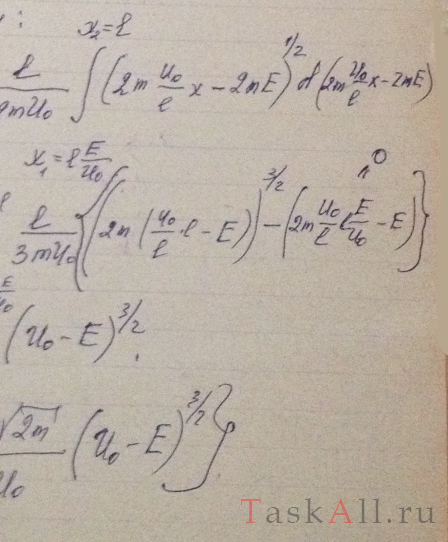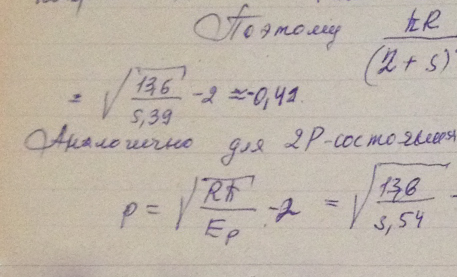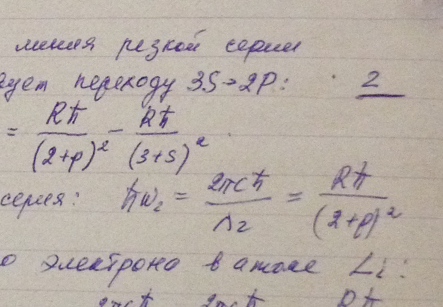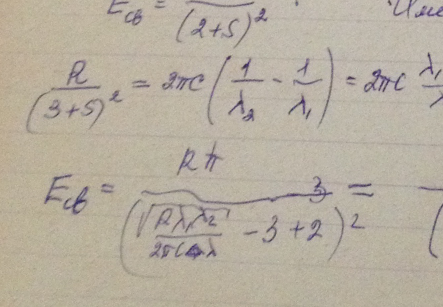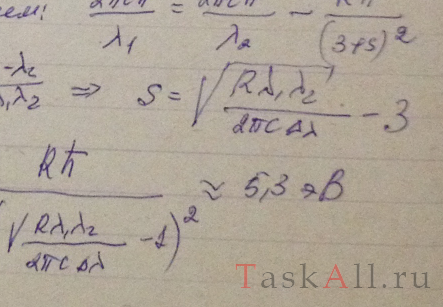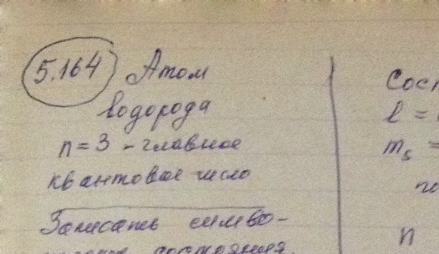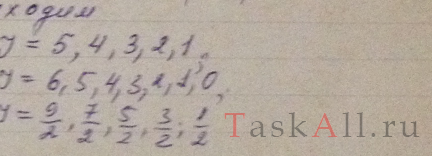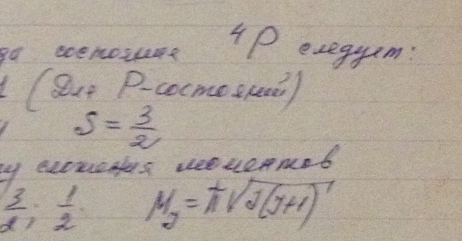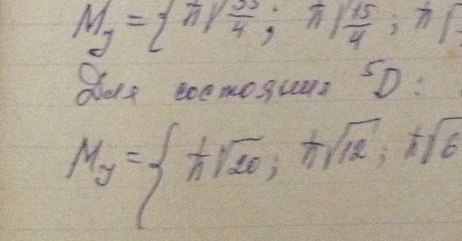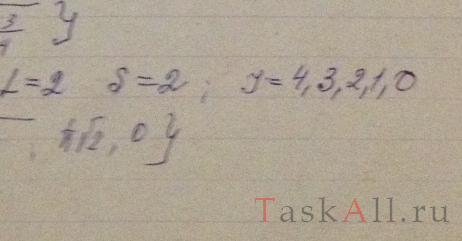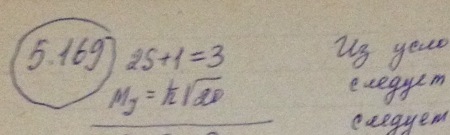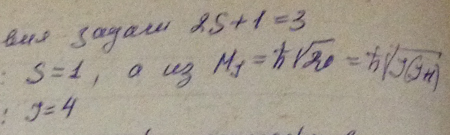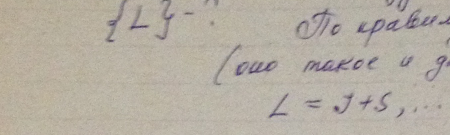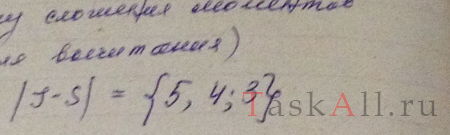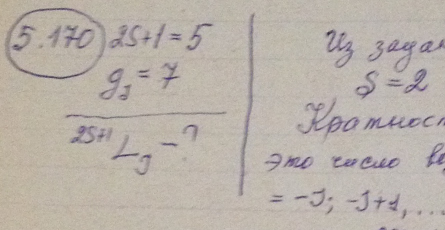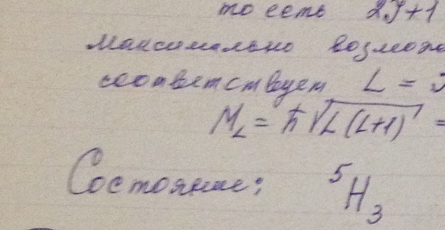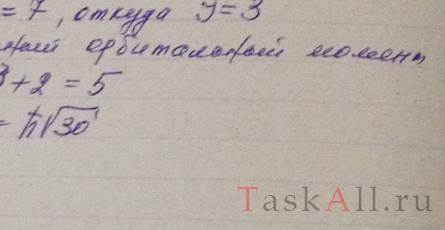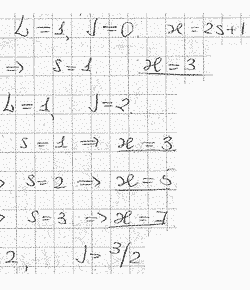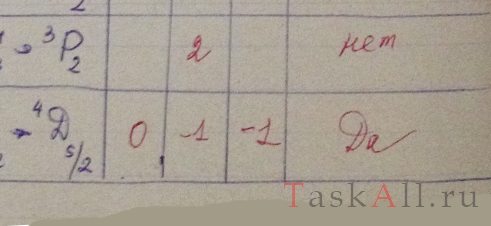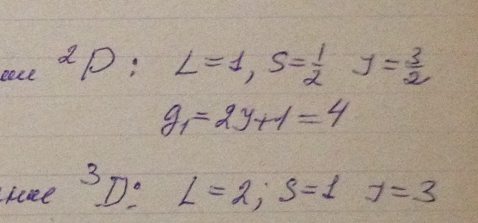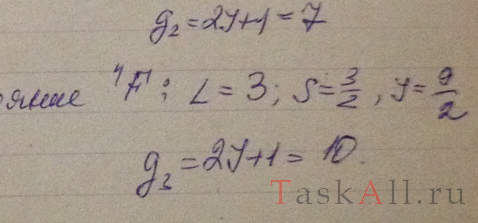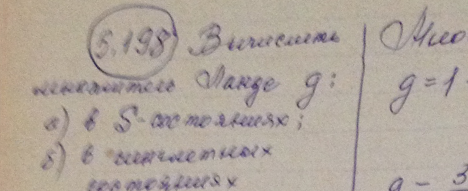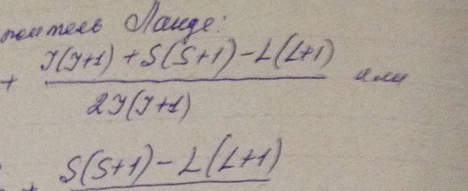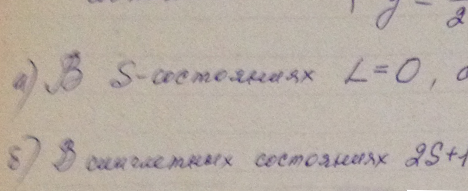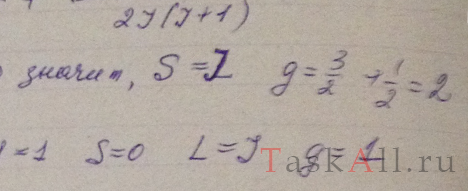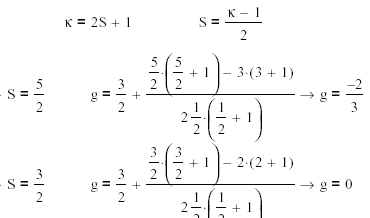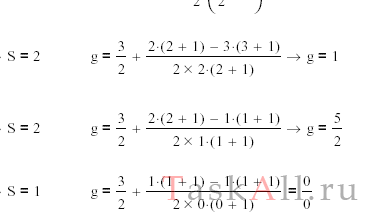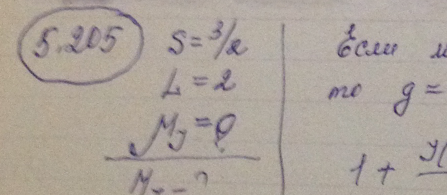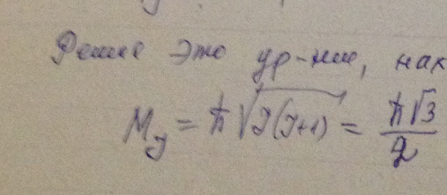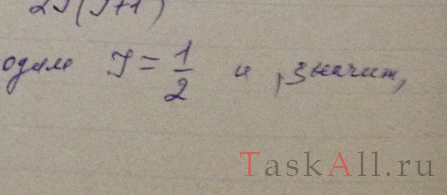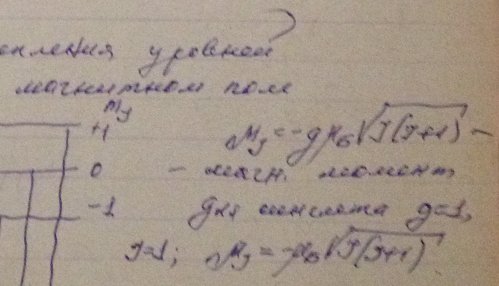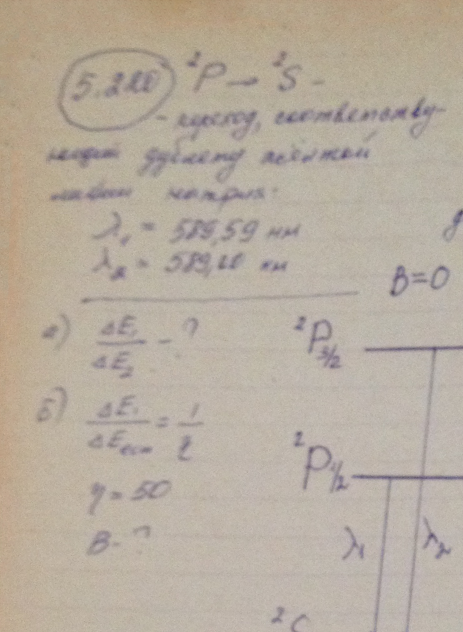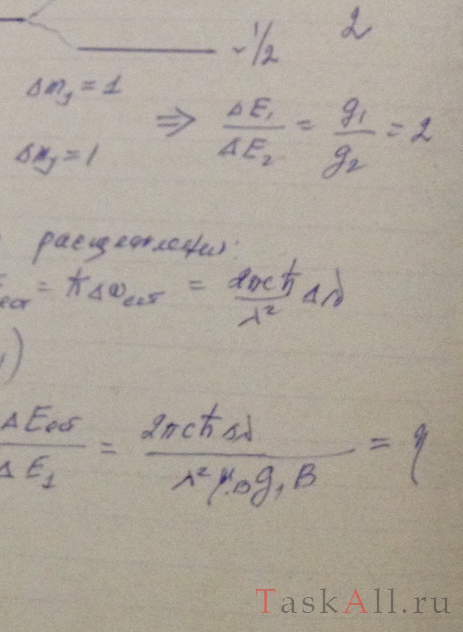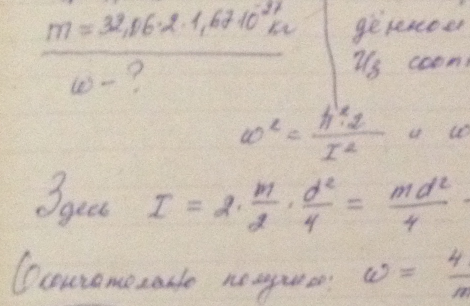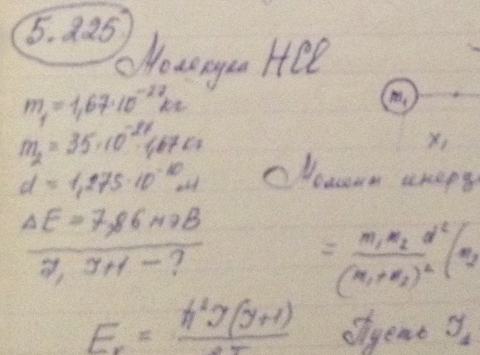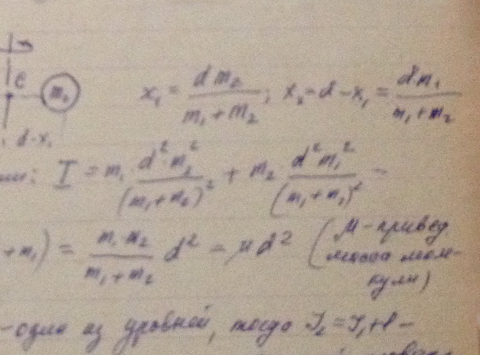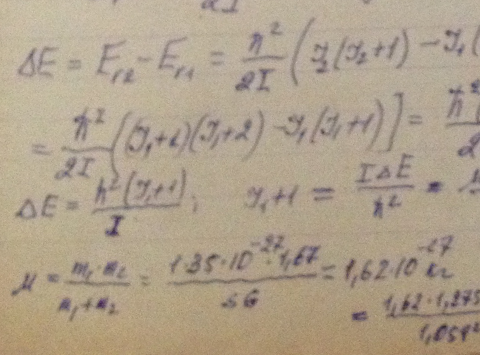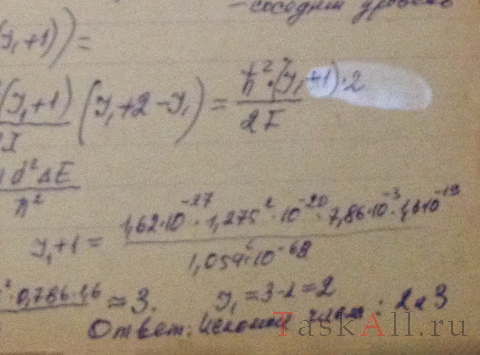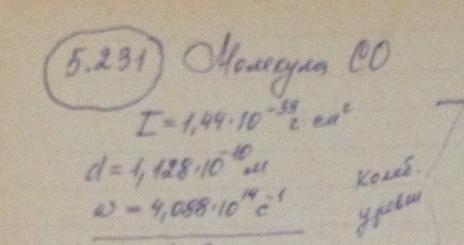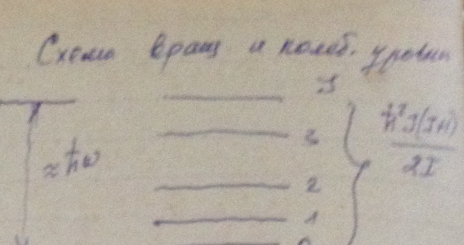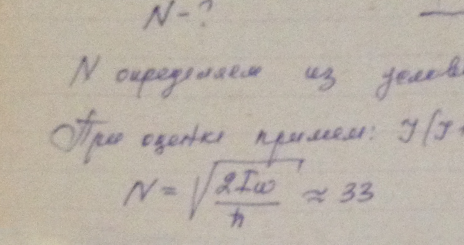  Частица движется слева в одномерном потенциальном поле, показанном на рис. 5.2. Левее барьера, высота которого U = 15 эВ, кинетическая энергия частицы К = 20 эВ. Как и во сколько раз изменится дебройлевская длина волны частицы при переходе через барьер?

Решение:

  Найти дебройлевскую длину волны релятивистских электронов, подлетающих к антикатоду рентгеновской трубки, если длина волны коротковолновой границы сплошного рентгеновского спектра λ_к = 10,0 пм.

Решение:

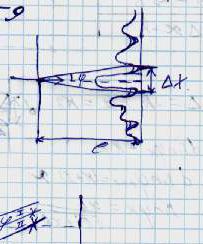
  Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью ширины b = 1,0 мкм. Определить скорость этих электронов, если на экране, отстоящем от щели на расстояние l = 50 см, ширина центрального дифракционного максимума ∆х = 0,36 мм.

Решение:

  Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью ширины b = 1,0 мкм. Определить скорость этих электронов, если на экране, отстоящем от щели на расстояние l = 50 см, ширина центрального дифракционного максимума Δx = 0,36 мм.

Решение:

  Частица массы m движется в одномерном потенциальном поле U = kx²/2 (гармонический осциллятор). Оценить с помощью соотношения неопределенностей минимально возможную энергию частицы в таком поле.

Решение:

  Оценить с помощью соотношения неопределенностей неопределенность скорости электрона в атоме водорода, полагая размер атома l = 0,10 нм. Сравнить полученную величину со скоростью электрона на первой боровской орбите данного атома.

Решение:

  Параллельный поток электронов, ускоренных разностью потенциалов U = 25 В, падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми d = 50 мкм. Определить расстояние между соседними максимумами дифракционной картины на экране, расположенном на расстоянии l = 100 см от щелей.

Решение:

  Оценить наименьшие ошибки, с которыми можно определить скорость электрона, протона и шарика массы 1 мг, если координаты частиц и центра шарика установлены с неопределенностью 1 мкм.

Решение:

  Электрон находится в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Найти ширину ямы, если разность энергии между уровнями с n_{1 = 2 и n2 = 3 составляет ∆E = 0,30 эВ.}

Решение:

  Волновая функция частицы массы m для основного состояния в одномерном потенциальном поле U(x) = kx²/2 имеет вид ψ = Ae^-αx2, где А — нормировочный коэффициент, α — положительная постоянная. Найти с помощью уравнения Шрёдингера постоянную α и энергию E частицы в этом состоянии.

Решение:

  Найти возможные значения энергии частицы массы m, находящейся в сферически-симметричной потенциальной яме U(r) = 0 при r < r₀ и U (r₀) = ∞, для случая, когда движение частицы описывается волновой функцией ψ(r), зависящей только от радиуса r. Указание. При решении уравнения Шрёдингера воспользоваться подстановкой ψ(r) = χ(r)/r.

Решение:

  Электрон атома водорода находится в состоянии, описываемом волновой функцией ψ(x) = Аехр(-r/r<sub1< sub="">), где А и r₁ — некоторые постоянные. Найти значения: а) нормировочного коэффициента А; б) энергии Е электрона и r₁ (с помощью уравнения Шрёдингера).</sub1<>

Решение:

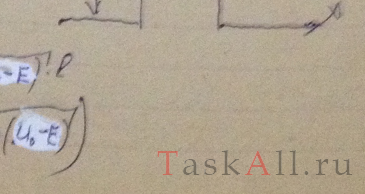
  Воспользовавшись формулой (5.3 е), найти для электрона с энергией Е вероятность D прохождения сквозь потенциальный барьер, ширина которого l и высота U₀ (рис. 5.7).

Решение:

  То же, что и в предыдущей задаче, но барьер имеет вид, показанный на рис. 5.8.

Решение:

  Энергия связи валентного электрона атома лития в состояниях 2S и 2Р равна 5,39 и 3,54 эВ. Вычислить ридберговские поправки для S- и Р-термов этого атома.

Решение:

  Найти энергию связи валентного электрона в основном состоянии атома лития, если известно, что длина волны головной линии резкой серии λ₁ = 813 нм и длина волны коротковолновой границы этой серии λ₂ = 350 нм.

Решение:

  Выписать спектральные обозначения термов атома водорода, электрон которого находится в состоянии с главным квантовым числом n = 3.

Решение:

  Сколько и какие значения квантового числа J может иметь атом в состоянии с квантовыми числами S и L, равными соответственно: а) 2 и 3; б) 3 и 3; в) 5/2 и 2?

Решение:

  Найти возможные значения полных механических моментов атомов, находящихся в состояниях 4Р и 5D.

Решение:

  Атом находится в состоянии, мультиплетность которого равна трем, а полный механический момент ћsqrt(20). Каким может быть соответствующее квантовое число L?

Решение:

  Определить максимально возможный орбитальный механический момент атома в состоянии, мультиплетность которого равна пяти и кратность вырождения по J - семи. Написать спектральное обозначение такого терма.

Решение:

  Найти возможные мультиплетности χ термов вида: a) ^χS₀, б) ^χP₂, в) ^χD_3/2, г) ^χF_1/2.

Решение:

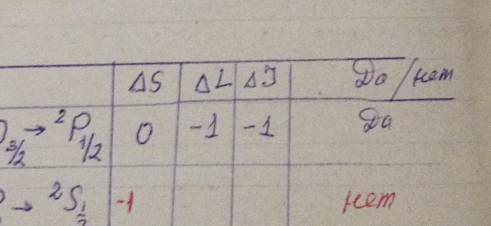
  Какие переходы запрещены правилами отбора: ²D_3/2 → ²P_1/2; ³P₁ → ²S_1/2; ³F₃ → ³P₂; ⁴F_7/2 → ⁴D_5/2?

Решение:

  Определить суммарную кратность вырождения 3D - состояния атома лития. Каков физический смысл этой величины?

Решение:

  Найти кратность вырождения состояний 2Р, 3D и 4F с максимально возможными полными механическими моментами.

Решение:

  Вычислить фактор Ланде для атомов: а) в S-состояниях; б) в синглетных состояниях.

Решение:

  Вычислить фактор Ланде для следующих термов: a) ⁶F_1/2; б) ⁴D_1/2; в) ⁵F₂; г) ⁵P₁; д) ³P₀.

Решение:

  Найти полный механический момент атома в состоянии с S = 3/2 и L = 2, если известно, что магнитный момент его равен нулю.

Решение:

  Некоторый атом находится в состоянии, для которого S = 2, полный механический момент М = sqrt(2) h, а магнитный момент равен нулю. Написать спектральный символ соответствующего терма.

Решение:

  На сколько подуровней расщепится в слабом магнитном поле терм: а) ³P₀; б) ²F_5/2 ;в) ⁴D_1/2

Решение:

  Известно, что спектральная линия λ = 612 нм обусловлена переходом между синглетными термами атома. Вычислить интервал ∆λ между крайними компонентами этой линии в магнитном поле с индукцией В = 10,0 кГс.

Решение:

  Длины волн дублета желтой линии натрия ( ²P → ²S ) равны 589,59 и 589,00 нм. Найти: а) отношение интервалов между соседними подуровнями зеемановского расщепления термов ²Р_3/2 и ²Р_1/2 в слабом магнитном поле; б) индукцию В магнитного поля, при которой интервал между соседними подуровнями зеемановского расщепления терма ²Р_3/2 будет в η = 50 раз меньше естественного расщепления терма ²Р.

Решение:

  Определить угловую скорость вращения молекулы S₂ на первом возбужденном вращательном уровне.

Решение:

  Найти для молекулы НСl вращательные квантовые числа двух соседних уровней, разность энергий которых равна 7,86 мэВ.

Решение:

  Оценить, сколько линий содержит чисто вращательный спектр молекул СО, момент инерции которых равен I = 1,44 · 10^-39 г · см^-2.

Решение:

  Найти отношение энергий, которые необходимо затратить для возбуждения двухатомной молекулы на первый колебательный и первый вращательный уровни. Вычислить это отношение для следующих молекул: а) H₂; б) HI; в) I₂.