Лабораторная работа №2

ФГБОУ ВО

«Уфимский государственный авиационный технический университет»

Кафедра ТК

ОТЧЕТ

по лабораторной работе № 2

по дисциплине «Теория принятия решения»

Вариант - 1

Выполнил: студенты гр. ИВТ-327Б

Проверил: доцент каф. ТК

Насыров Р.В.

Уфа 2023

Тема работы: Динамическое программирование

Цель работы: знакомство с детерминированными и вероятностными задачами динамического программирования, изучение различных методов решения в системе компьютерной математики.

Задание:

Текст программы:

import random CountVar = 7 M = [[0 for i in range(CountVar)] for j in range(CountVar)] M[0][1] = random.randint(1, 20) M[0][2] = random.randint(1, 20) M[1][2] = random.randint(1, 20) M[1][3]= random.randint(1, 20) M[1][4]= random.randint(1, 20) M[2][5] = random.randint(1, 20) M[2][3]= random.randint(1, 20) M[2][4]= random.randint(1, 20) M[3][4] = random.randint(1,20) M[3][5]= random.randint(1, 20) M[3][6]= random.randint(1, 20) M[4][5]= random.randint(1, 20) M[4][6]= random.randint(1, 20) M[5][6]= random.randint(1,20) for i in range(CountVar): for j in range(CountVar): if i == j: M[i][j] = "-" minp = [100 for i in range (CountVar)] for i in range(CountVar): for j in range(CountVar): print(M[i][j], end="\t") print() pravo = { 0: [7], 1: [6, 7], 2: [5, 6, 7], 3: [4, 5, 6,7], 4: [ 3,4,5, 6], 5: [2,3] } levo= { 0: [6,7], 1: [5,6, 7], 2: [4, 5, 6], 3: [3,4, 5, 6], 4: [ 2,3], 5: [1] } v = [] start=1 otvet=0 for k in range(CountVar-1): print() print("x", k, "|\t\t\t\t\t\t\t\t") print("\t|", end=" ") for i in range(len(pravo[k])): print(pravo[k][i], end="\t|\t") print("f(x)|\tx*\t") print("---------------------------------------------------------------------------") for i in range(len(levo[k])): min=100 ans = [0 for z in range(7)] print(levo[k][i], "\t|", end="") for j in range(len(pravo[k])): if pravo[k][j] == levo[k][i]: if minp[levo[k][i]-1]==100: print(" ", 0, "\t|", end="") else: print(" ",minp[levo[k][i]-1],"\t|", end="") else: if start==1: minp[5]=M[levo[k][i] - 1][pravo[k][j] - 1] ans[pravo[k][j] - 1] += M[levo[k][i] - 1][pravo[k][j] - 1] min = ans[pravo[k][j] - 1] print(' ', ans[pravo[k][j] - 1], "\t|", end="") start-=1 elif M[levo[k][i] - 1][pravo[k][j] - 1] ==0: print(' ----', "\t|", end="") elif M[levo[k][i] - 1][pravo[k][j] - 1] != "-": ans[pravo[k][j] -1]+=M[levo[k][i] - 1][pravo[k][j] - 1]+minp[pravo[k][j]-1] if minp[pravo[k][j]-1]==100: ans[pravo[k][j] - 1]-=100 if ans[pravo[k][j] -1]<=min and ans[pravo[k][j] -1]!=0: min=ans[pravo[k][j] -1] print(' ',ans[pravo[k][j] -1], "\t|", end="") minp[levo[k][i]-1]=min if minp[levo[k][i]-1]==100: print(" ",minp[levo[k][i]-1]-100, "\t|", end="") else: print(" ", minp[levo[k][i]-1], "\t|", end="") otvet=minp[levo[k][i]-1] for j in range(len(pravo[k])): if pravo[k][j] == levo[k][i]: print(" ",pravo[k][j], "\t|", end="") for i in range(len(ans)): if min==ans[i]: print(" ", i+1, "\t|", end="") v.append(i+1) print() v.append(1) print("Путь", set(sorted(v))) print("Длинна пути", otvet)

Работа программы:

Реализация №1

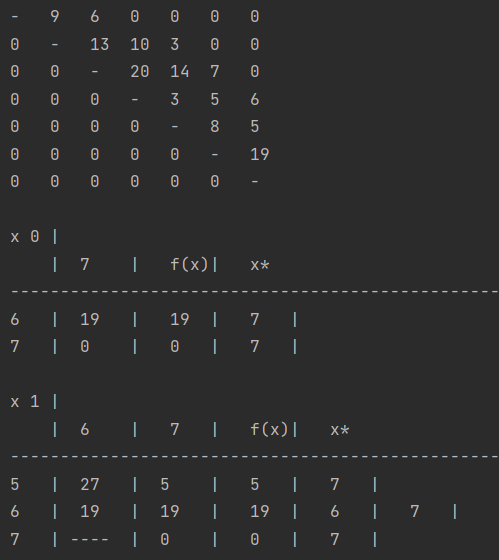
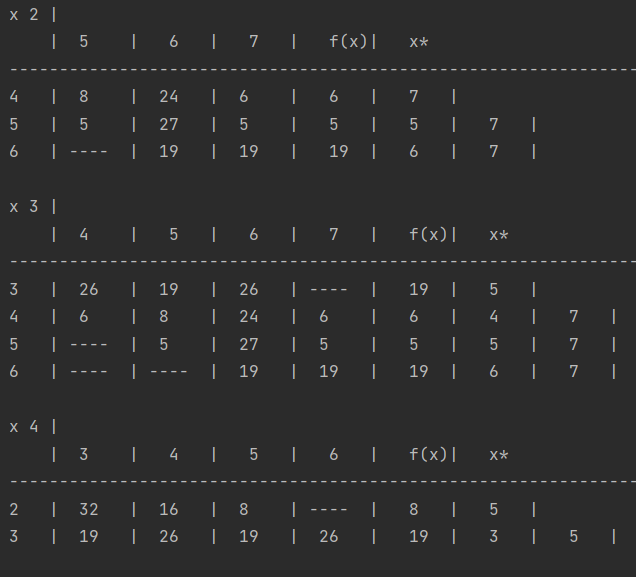
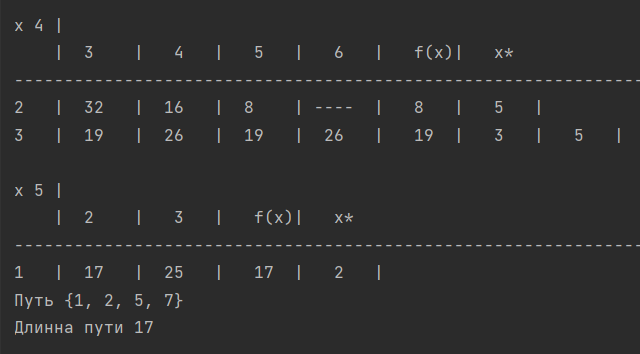
Проверяем путь по таблицам x1-x5.

Данную задачу можно решить за 3 этапа, тогда:

По таблице x5 смотрим путь из 1 в 2.

По таблице x4 смотрим путь из 2 в 5.

По таблице x3 смотрим путь из 5 в 7.

Проверяем правильность вычисления по исходной матрице.9+3+5 = 17

Также можно пройти за 4,5,6 этапов, если оставаться в промежуточных вершинах 5 или 7.

Реализация №2

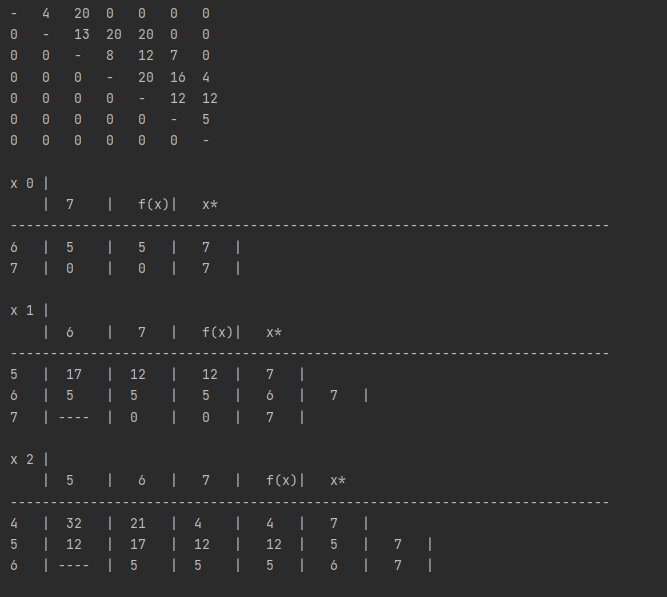
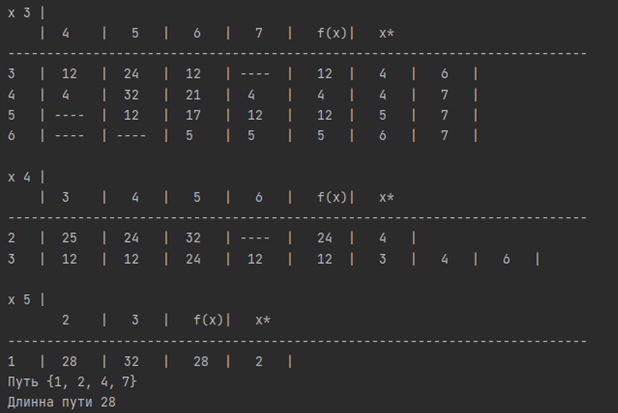
Проверяем путь по таблицам x1-x5.

Данную задачу можно решить за 3 этапа, тогда:

По таблице x5 смотрим путь из 1 в 2.

По таблице x4 смотрим путь из 2 в 4.

По таблице x3 смотрим путь из 4 в 7.

Проверяем правильность вычисления по исходной матрице.4+20+4 = 28

Также можно пройти за 4,5,6 этапов, если оставаться в промежуточных вершинах 4 или 7.

Реализация №3

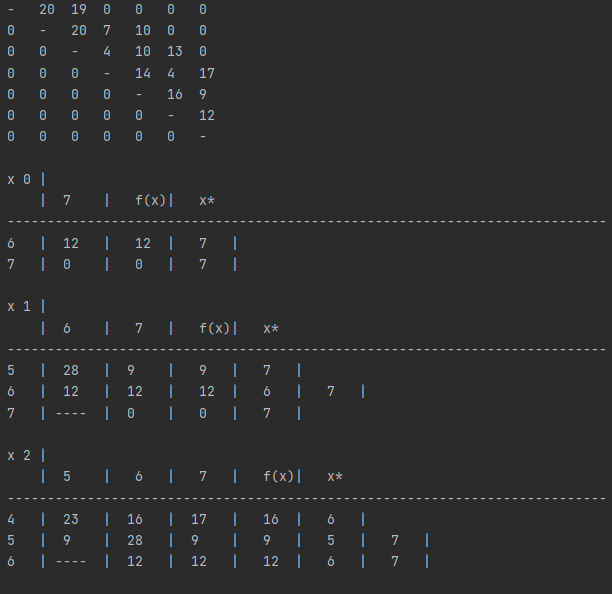
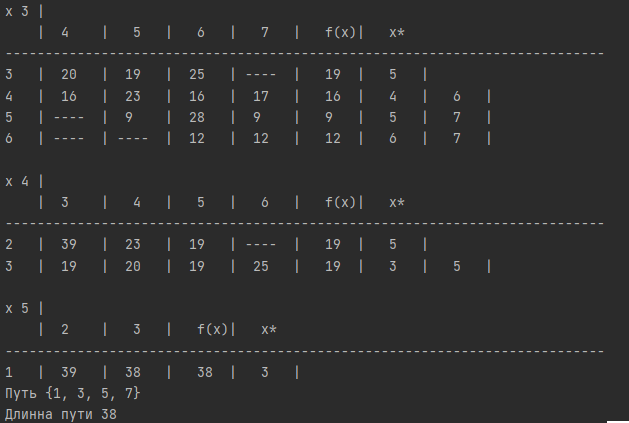
Проверяем путь по таблицам x1-x5.

Данную задачу можно решить за 3 этапа, тогда:

По таблице x5 смотрим путь из 1 в 2.

По таблице x4 смотрим путь из 2 в 4.

По таблице x3 смотрим путь из 4 в 7.

Проверяем правильность вычисления по исходной матрице.19+10+9 = 38

Также можно пройти за 4,5,6 этапов, если оставаться в промежуточных вершинах 5 или 7.

Вывод:

В ходе выполнения лабораторной работы, мы ознакомились с детерминированными и вероятностными задачами динамического программирования, изучили различные методы решения в системе компьютерной математики.