Чтобы определить, связаны ли данные метрики, можно провести анализ корреляции между ними, построить поле рассеяния и оценить, насколько тесно они взаимосвязаны. Если корреляция между ними окажется высокой, то, возможно, одна из метрик может частично или полностью заменять другую. Если же корреляция невелика, обе метрики необходимо учитывать, так как они, вероятно, описывают различные аспекты надежности сети.

Код программы:

import networkx as nx import numpy as np import matplotlib.pyplot as plt from scipy.stats import pearsonr, spearmanr # Функция для оценки запаса структурной надежности для ориентированного графа def structural_reliability_margin(G): initial_edges = G.number_of_edges() for edge in list(G.edges): G.remove_edge(*edge) if not nx.is_strongly_connected(G): # Проверяем сильную связность G.add_edge(*edge) remaining_edges = G.number_of_edges() return remaining_edges / initial_edges # Функция для расчета средней степени центральности в ориентированном графе def centrality_degree(G): centrality = nx.in_degree_centrality(G) # Входная степень центральности return np.mean(list(centrality.values())) # Генерация случайных графов и расчет метрик num_graphs = 30 structural_reliability = [] centrality = [] for i in range(num_graphs): print(f"\nЭксперимент {i + 1}") # Генерируем случайный ориентированный граф с вероятностью ребра p G = nx.erdos_renyi_graph(n=20, p=0.2, directed=True) # Ориентированный граф # Вывод матрицы смежности графа adjacency_matrix = nx.adjacency_matrix(G).todense() print(f"Матрица смежности графа {i + 1}:\n", adjacency_matrix) # Рассчитываем запас структурной надежности reliability = structural_reliability_margin(G) structural_reliability.append(reliability) print(f"Запас структурной надежности графа {i + 1}: {reliability}") # Рассчитываем среднюю степень центральности centrality_score = centrality_degree(G) centrality.append(centrality_score) print(f"Степень центральности графа {i + 1}: {centrality_score}") # Вычисляем корреляцию if len(structural_reliability) > 1 and len(centrality) > 1: pearson_corr, _ = pearsonr(structural_reliability, centrality) spearman_corr, _ = spearmanr(structural_reliability, centrality) print(f"\nКоэффициент корреляции Пирсона: {pearson_corr}") print(f"Коэффициент корреляции Спирмена: {spearman_corr}") if abs(pearson_corr) > 0.7 or abs(spearman_corr) > 0.7: print("\nВывод: Метрики имеют сильную корреляцию, возможно, одна из них избыточна.") else: print("\nВывод: Метрики слабо коррелированы, рекомендуется считать обе для полноты анализа.") # Построение поля рассеяния plt.scatter(structural_reliability, centrality, color='blue', alpha=0.7) plt.xlabel('Запас структурной надежности') plt.ylabel('Степень центральности') plt.title('Поле рассеяния для гипотетических метрик (ориентированный граф)') plt.show()

Граф :

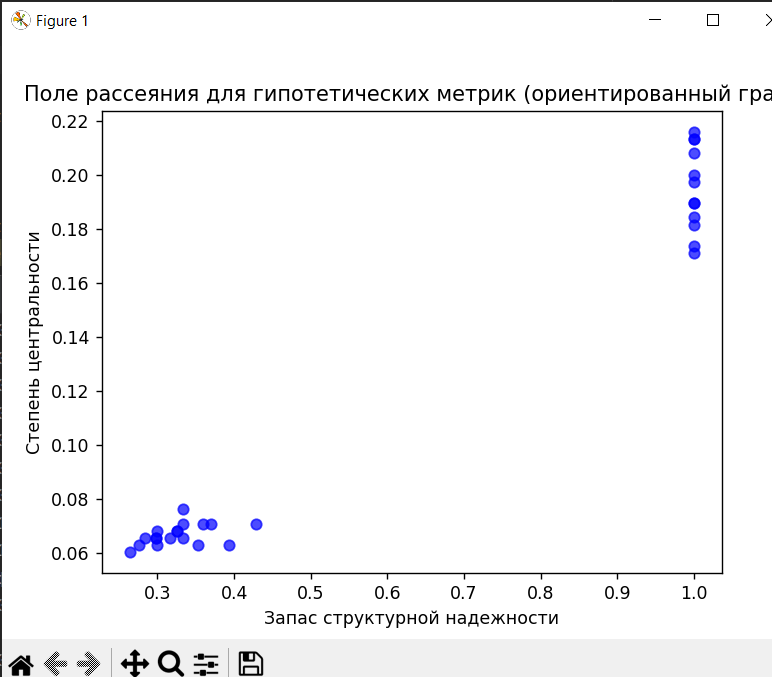
Вывод:

Запас структурной надежности — это мера того, какую долю ребер можно удалить из графа без потери его связности. Это указывает на то, насколько устойчив граф к потерям ребер (в контексте сетей, например, к поломкам или отказам компонентов).

Алгоритм для расчета:

- Изначально мы получаем количество ребер в графе до удаления.

- Для каждого ребра в графе мы его удаляем и проверяем, сохраняет ли граф свою связность .

- Если граф остается сильно связным (в случае ориентированного графа), то ребро можно безопасно удалить.

- Если граф не остаётся связным , то это означает, что удаление ребра нарушает связность сети, и ребро восстанавливается.

- Затем рассчитываем остаточное количество ребер (которые не повлияли на связность) и находим отношение оставшихся ребер к начальному количеству.

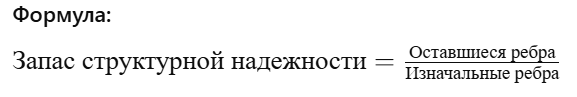
Это отношение показывает, насколько граф устойчив к удалению ребер. Чем больше это значение, тем более устойчив граф.