Управление качеством / 6 семестр / практики / 5

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра технической кибернетики

ОТЧЕТ по практической работе

по дисциплине: «Всеобщее управление качеством»

Вариант – 24

Выполнил: ст. гр. ИВТ-327Б

Проверил: профессор кафедры ТК

Гвоздев В. Е.

Уфа 2024

Цель работы: Изучить методы преобразования субъективных словесных оценок к виду количественных оценок при построении формальных математических моделей.

Задание на работу

а) Построить диаграммы рассеяния для различных пар параметров состояния (см. варианты заданий);

б) Рассчитать значения коэффициентов корреляции между указанными параметрами состояния и оценить реальность связи, а также доверительные интервалы, в которых с данным уровнем q находятся истинные значения коэффициента корреляции q;

в) Рассчитать параметры линейной зависимости и рассчитать доверительные границы для параметров _Y/X.

Исходные данные:

x	y
267,50	828,00
682,60	1163,40
915,30	2110,70
256,50	713,80
204,60	945,30
34,60	356,40
1,00	454,30
108,10	462,80
197,30	557,80
110,50	520,70
122,80	529,80
208,60	784,20
58,40	310,20
140,20	505,50
119,80	397,00
103,40	471,30
76,63	367,80
7,70	169,80
47,70	202,20
7,30	44,10
55,15	176,47
50,20	168,50
117,19	289,89
43,18	144,95
30,70	110,51
323,59	715,64

Ход работы:

Найдем коэффициент корреляции, для этого высчитаем:

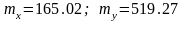
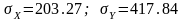
Тогда коэффициент корреляции равен

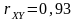
Составим уравнение линейной зависимости y=203+2x, тогда диаграмма рассеяния:

Рассчитаем оценку для среднего квадратического отклонения r от :

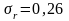
Тогда коэффициента регрессии будем иметь:

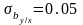
Определим следующие доверительные интервалы:

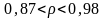
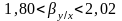
Контрольные вопросы

1. Что характеризует коэффициент корреляции?

Коэффициент корреляции характеризует степень линейной взаимосвязи случайных величин X и Y, причем

.

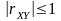2. Чем обусловлена необходимость интервального оценивания значений коэффициента корреляции?

Интервальное оценивание позволяет учесть случайную изменчивость и оценить диапазон значений, в пределах которого, с некоторой вероятностью, находится истинное значение коэффициента корреляции.

3. Какова содержательная интерпретация среднеквадратического отклонения?

Среднеквадратическое отклонение - показатель рассеивания значений случайной величины. Большое значение среднеквадратического отклонения показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.