- •Гидродинамическое сопротивление трубопровода
- •Что понимают в гидродинамике под реальной и идеальной жидкостью?
- •В чём принципиальное различие в понятиях «идеальный газ» в термодинамике и «идеальная жидкость» в гидродинамике?
- •На какие два вида подразделяют реальные жидкости?
- •Какую величину называют геометрическим напором?
- •Какую величину называют гидростатическим (пьезометрическим) напором? Какой физический смысл имеют геометрический и пьезометрический напоры?
- •На компенсацию каких потерь затрачивается энергия при течении жид костей по трубопроводам? в какую форму переходит механическая энергия потока, теряемая при движении?
- •Для какой цели на трубопроводе используется диафрагма?
- •Для чего служат дифманометры?
- •Почему в качестве манометрических жидкостей в дифманометрах используют не только воду, но и другие жидкости?
- •Что понимают под местным сопротивлением?
- •Изучение работы центробежного насоса
- •Устройство и принцип работы одно- и многоступенчатых центробежных насосов. Область применения.
- •Почему центробежный насос требуется заполнять при пуске?
- •Для каких целей на конце всасывающей трубы размещают клапан с сеткой?
- •Назовите параметры, характеризующие работу центробежного насоса.
- •Какой напор и какую производительность создают одно- и многосту пенчатые насосы?
- •Какие ещё (кроме центробежного) насосы применяются в химической промышленности?
- •Как работает поршневой (плунжерный) насос? Его достоинства и недостатки, область применения.
- •Что такое напор и каким уравнением описывается напор насоса?
- •Теплопередача в кожухотрубчатом стеклянном теплообменнике
- •Каковы физический смысл и единицы измерения коэффициента тепло передачи?
- •Достоинства и недостатки плёночных абсорбционных аппаратов.
- •Простая перегонка (вопрос 9, 10)
- •В чём сущность и какова физическая основа простой перегонки? Что та кое фракционная перегонка?
- •Почему при простой перегонке невозможно достичь полного разделения нк и вк?
- •Получите уравнение простой перегонки. Почему это уравнение, наряду с уравнениями баланса по всему веществу и баланса по нк, применяется для расчёта процесса?
- •Какие основные элементы содержит любая установка простой перегонки?
- •Как объяснить начало псевдоожижения и уноса частиц исходя из равновесия сил?
- •1. Силы, действующие на частицы
- •2. Начало псевдоожижения
- •3. Унос частиц
Гидродинамическое сопротивление трубопровода
Что понимают в гидродинамике под реальной и идеальной жидкостью?
Идеальная жидкость — это модель жидкости, которая не имеет вязкости и не сжимается.
В потоке идеальной жидкости в отличие от реальной будут действовать только нормальные напряжения (в реальной действуют еще и касательные, то есть имеет место быть внутреннее трение в жидкости). При движении реальной жидкости в ней возникают силы внутреннего трения, отказывающие сопротивление движению. Силы возникают между слоями жидкости при их движении друг относительно друга.
В чём принципиальное различие в понятиях «идеальный газ» в термодинамике и «идеальная жидкость» в гидродинамике?
Идеальная жидкость несжимаема в отличие от идеального газа.
Идеальный газ в термодинамике — это теоретическая модель газа, в которой пренебрегают размерами и взаимодействиями частиц газа и учитывают лишь их упругие столкновения. Внутренняя энергия идеального газа определяется лишь кинетической энергией его частиц.
Идеальная жидкость в гидродинамике — это воображаемая жидкость, лишённая вязкости и теплопроводности. В природе таких жидкостей не существует, но решение ряда теоретических вопросов в гидравлике значительно облегчается при использовании идеальной жидкости.
На какие два вида подразделяют реальные жидкости?
Капельные жидкости (несжимаемые, обычные жидкости), упругие (пары и газы).
Какую величину называют геометрическим напором?
Уравнение Бернулли или основное уравнение гидростатики имеет вид:
Физический смысл слагаемых
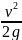 – кинетическая
энергия (динамический напор)
– кинетическая
энергия (динамический напор)
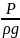 – удельная
потенциальная энергия столба жидкости
(пьезометрический напор)
– удельная
потенциальная энергия столба жидкости
(пьезометрический напор)
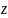 – положение
точки на линии тока, нивелирная высота,
удельная потенциальная энергия положения
(геометрический напор)
– положение
точки на линии тока, нивелирная высота,
удельная потенциальная энергия положения
(геометрический напор)
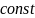 – величина,
меняющаяся для различных линий тока
– величина,
меняющаяся для различных линий тока
Какую величину называют гидростатическим (пьезометрическим) напором? Какой физический смысл имеют геометрический и пьезометрический напоры?
См. 1.4.
Запишите уравнение Бернулли применительно к двум произвольным поперечным сечениям потока реальной капельной жидкости в трубопроводе. Каковы размерность и физический смысл каждого из членов уравнения Бернулли?
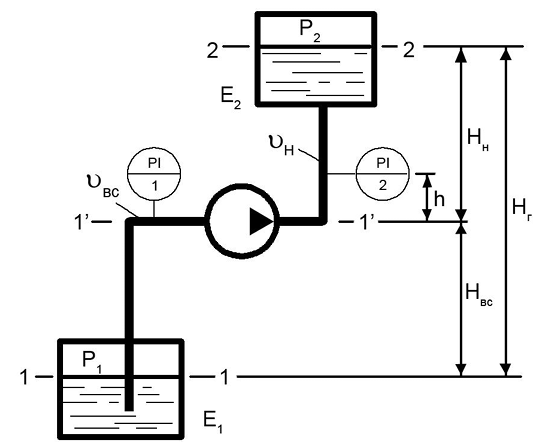
Запишем уравнение баланса энергии для сечений 1-1 и 1’-1’.
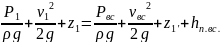
Физ. смысл см в 1.4.
На компенсацию каких потерь затрачивается энергия при течении жид костей по трубопроводам? в какую форму переходит механическая энергия потока, теряемая при движении?
Потери на преодоление сил трения (потери напора по длине или потери на гидравлическое трение). Они определяются работой сил трения внутри жидкости и сил трения жидкости о твёрдые поверхности и пропорциональны длине пути, пройденного жидкостью.
Местные потери напора (потери в местных гидравлических сопротивлениях). Это затраты удельной энергии на преодоление местных гидравлических сопротивлений, вызванных изменением формы потока и размеров живого сечения. К местным сопротивлениям относятся вход в трубопровод и выход из него, сужения и расширения потока, отводы (повороты трубопровода), соединительные колена, тройники, диафрагмы и другие измерительные устройства, вентили, краны, задвижки и прочая запорно-регулировочная арматура.
Механическая энергия потока, теряемая при движении, переходит в тепловую. Это происходит из-за вязкости жидкости, которая вызывает гидравлические потери.
Для какой цели на трубопроводе используется диафрагма?
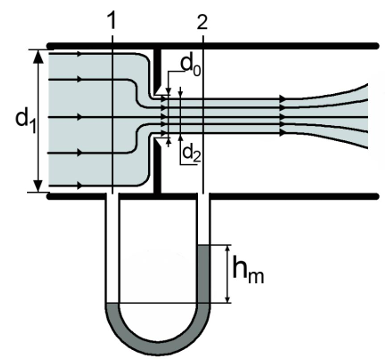
Диафрагма
используется для определения скоростей
и расходов в трубопроводах. Она
представляет собой тонкий металлический
диск с круглым отверстием посередине,
размещаемый внутри трубы, поперек
потока. Диаметр отверстия диафрагмы
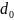 значительно меньше диаметра
значительно меньше диаметра
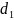 трубы, на которой устанавливается
диафрагма. За диафрагмой струя жидкости
продолжает сжиматься, поэтому на
некотором расстоянии за диафрагмой при
максимальном сжатии потока диаметр
струи становится 4 равным
трубы, на которой устанавливается
диафрагма. За диафрагмой струя жидкости
продолжает сжиматься, поэтому на
некотором расстоянии за диафрагмой при
максимальном сжатии потока диаметр
струи становится 4 равным
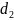 ,
причем
,
причем
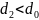 .
К сечениям 1 и 2 присоединен U- образный
дифманометр. Найдем разность давлений
в сечениях 1 и 2, используя уравнение
Бернулли:
.
К сечениям 1 и 2 присоединен U- образный
дифманометр. Найдем разность давлений
в сечениях 1 и 2, используя уравнение
Бернулли:
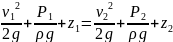
С
учетом того, что
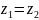 ,
уравнение можно записать следующим
образом:
,
уравнение можно записать следующим
образом:
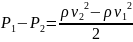
Перепад давления в трубопроводе через показания U-образного дифманометра:
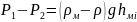
Также из условия постоянства объемных расходов капельных жидкостей следует:
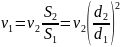
Откуда
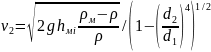
Скорость
жидкости в отверстии диафрагмы
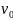 определяет значение скорости
определяет значение скорости
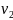 .
.
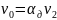
где
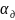 – коэффициент расхода диафрагмы.
– коэффициент расхода диафрагмы.
Тогда объемный расход жидкости в отверстии диафрагмы и в трубе:
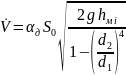
Можно
также использовать формулу
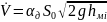 .
.
С целью снижения гидравлических потерь на острых кромках диафрагмы вместо нее для определения расходов жидкостей могут устанавливаться сопла с гладким входом.