2. Вопросы без вывода

1. Перечислите (с соответствующими пояснениями) характеристики слоя зернистого материала. Какова связь между эквивалентным диаметром канала в слое и размером частиц?

При расчетах и проектировании аппаратов с неподвижными зернистыми слоями определяют гидравлическое сопротивление этих слоев , Па. Его рассчитывают по следующей зависимости:

где – общий коэффициент трения (учитывает потери давления на трение и на местные сопротивления); – средняя длина каналов в слое, м; – эквивалентный диаметр каналов в слое, м; – плотность среды в каналах слоя, кг/м³; – скорость среды в каналах слоя, м/с.

Эквивалентный диаметр каналов определяют через удельную поверхность слоя , м²/м³, и его относительный свободный объем (порозность) , м³/м³. Данные параметры вычисляются с использованием суммарной поверхности всех частиц слоя , объема частиц в слое , суммарного периметра каналов , высоты слоя , фактора формы и коэффициент кривизны каналов (все перечисленные параметры также являются характеристиками зернистого слоя):

Для потока в слое различают действительную , и фиктивную , скорости. Фиктивная скорость – отношение объемного расхода среды ко всей площади поперечного сечения слоя, а действительная – отношение этого расхода к поперечному сечению каналов слоя. Поэтому:

Эквивалентный диаметр канала связан с размером частиц слоя:

После подстановки в уравнение (1.1) величин из (1.4)–(1.6) при :

Для движения потока через зернистый слой свойственны ламинарный и турбулентный режимы. Критерий Рейнольдса , характеризующий области существования различных режимов течения через слой, выражают:

Ламинарный режим существует при , автомодельность при турбулентном режиме наступает при .

Универсальная зависимость для расчета для всех режимов течения потока через зернистый слой:

При коэффициент трения можно рассчитать по зависимости:

При принимают:

41. Изобразите зависимость коэффициента сопротивления от числа Рейнольдса при движении жидкости в каналах между частицами неподвижного зернистого слоя. Сопоставьте эту зависимость с подобной при движении жидкости в прямых трубах.

Потеря давления

– коэффициент сопротивления; – действительная скорость жидкости

– доля свободного объема (порозность).

При ламинарном режиме , коэффициент Дарси: .

При наступает автомобильная область турбулентного режима движения в зернистом слое, когда можно пренебречь первым членом в правой части уравнения в этом случае

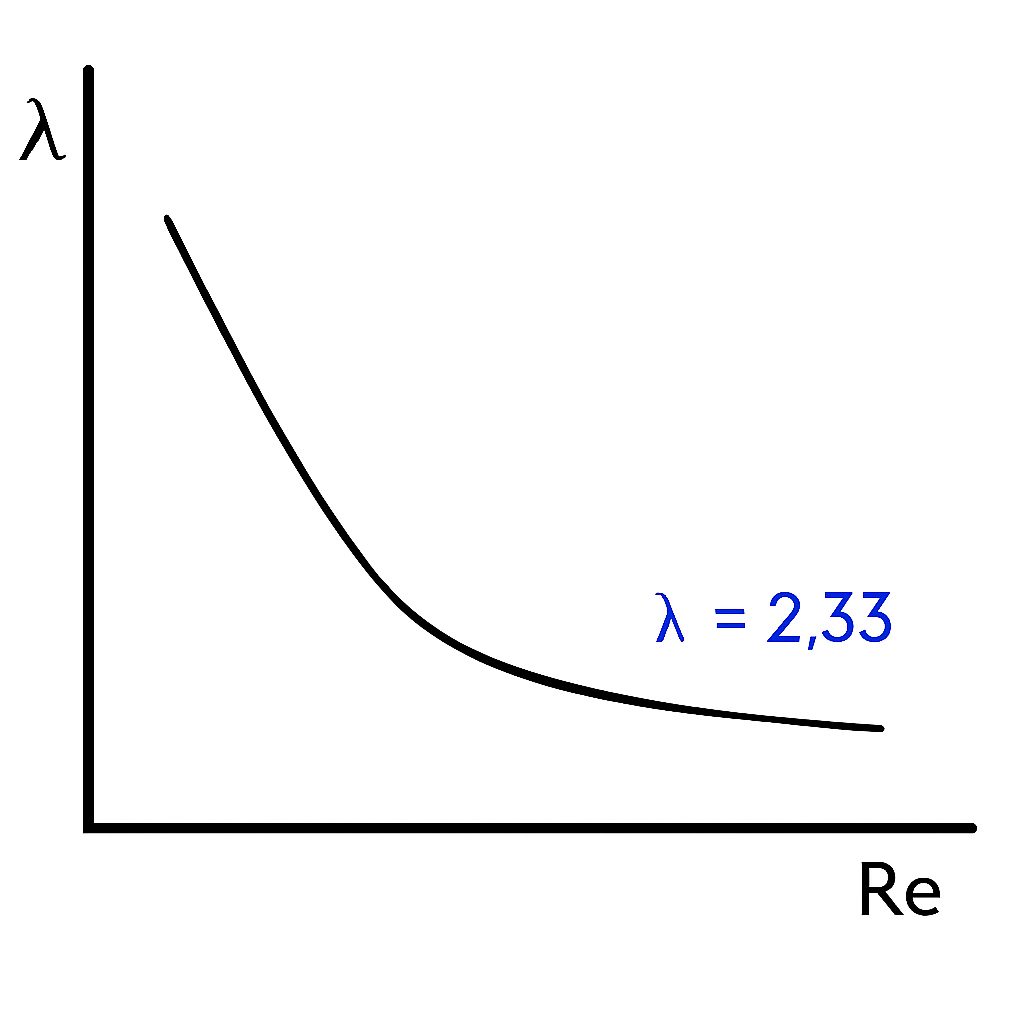
Рисунок 2.1 – Зависимость коэффициента Дарси от числа Рейнольдса

Потери давления описываются уравнением Эргуна:

42. Охарактеризуйте состояние слоя зернистого материала в зависимости от скорости восходящего потока газа или жидкости. Изобразите зависимости гидравлического сопротивления, высоты и порозности слоя от скорости потока.

Рисунок 3.1 – Движение газа (жидкости) через слой твердых частиц:

а – неподвижный; б – кипящий; в – унос частиц

З ернистый слой остается неподвижным только при небольших скоростях жидкостей или газов (рис. 3.1, а).

При достижении скорости начала псевдоожижения , слой перестаёт быть неподвижным, приобретает текучесть и переходит в кипящее (псевдоожиженное) состояние. В таком слое твёрдые частицы интенсивно перемещаются в потоке в различных направлениях (рис. 3.1, б), и весь слой напоминает кипящую жидкость.

При дальнейшем увеличении скорости потока высота слоя продолжает возрастать вплоть до того момента, когда скорость достигает нового критического значения (скорость уноса), при котором слой разрушается и твёрдые частицы начинают уноситься потоком (рис 3.1, в). Явление массового уноса твёрдых частиц потоком газа называют пневмотранспортом и используют в промышленности для перемещения сыпучих материалов.

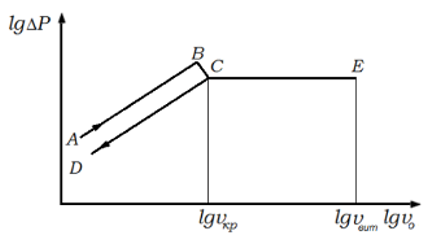
Рисунок 3.2 – Зависимость гидравлического сопротивления от скорости потока жидкости (или газа) в монодисперсном слое частиц.

С остояние зернистого слоя может быть представлено в виде зависимости гидравлического сопротивления слоя от скорости потока газа или жидкости (сплошной фазы), поступающего снизу под слой (рис. 3.2).

Рисунок 3.3 – Зависимость высоты слоя от скорости сплошной фазы

П о мере возрастания скорости потока сплошной фазы увеличивается гидравлическое сопротивление неподвижного слоя (линия AB или в обратном направлении линия ). Начало псевдоожижения (при скорости потока ) наступает при равенстве силы гидравлического сопротивления слоя весу всех его частиц. Данное условие выполняется для всей области существования псевдоожиженного слоя (линия ), вплоть до того момента, когда скорость становится такой, при которой слой разрушается и начинается массовый унос частиц потоком. Эту скорость называют скоростью свободного витания частиц (скоростью уноса) и обозначают символом .

43. Что называют «числом псевдоожижения»? Изложите последовательность расчёта диаметра аппарата для проведения процесса с псевдоожиженным слоем зернистого материала. Приведите формулу для расчёта гидравлического сопротивления этого аппарата.

Отношение рабочей скорости , величина которой должна находиться в пределах между (псевдоожижения) и (витания), к скорости начала псевдоожидения называют числом псевдоожижения и обозначают символом

Число псевдоожижения характеризует интенсивность перемешивания частиц и состояние псевдоожиженого слоя. Опытным путем найдено, что во многих случаях интенсивное перемешивание достигается уже при . Оптимальное значение устанавливаются обычно практически для каждого конкретного технологического процесса и могут меняться в довольно широких пределах.

В случае монодисперсного слоя для расчета скорости начала псевдоожижения можно воcпользоваться зависимостями

Скорость начала уноса, при которой происходят разрушение слоя и массовый унос частиц, определяют аналогично расчету скорости свободного осаждения частиц по уравнению, пригодному для всех режимов движения частиц:

При псевдоожижении по мере увеличения скорости потока увеличиваются его высота и порозность . Для расчета порозности можно использовать уравнение

которое применимо только к однородным псевдоожиженным слоям.

Обозначим через объем, высоту и порозность слоя в неподвижном состоянии, а через те же величины в псевдоожиженном состоянии. Поскольку объем твердого материала постоянен, то

Тогда

В аппарате постоянного поперечного сечения

Определив значение из уравнения (4.1), можно найти высоту псевдоожиженного слоя

необходимую при расчете высоты аппаратов, в которых зернистый материал находится в псевдоожиженном состоянии.

С учетом Архимедовых сил, действующих на частицы слоя, это выражение можно представить в виде:

где – плотность, порозность и высота неподвижного слоя соответственно.

При скорости начала псевдоожижения и выше сопротивление слоя сохраняет практически постоянное значение и зависимость выражается прямой линиейАВ, параллельной оси абсцисс. Это связано с тем, что с ростом скорости псевдоожижающего агента контакт между частицами сокращается и они получают большую возможность хаотического перемешивания по всем направлениям. При этом возрастает среднее расстояние между частицами, т.е. увеличиваются порозность слоя и его высота. Высоту расширившегося слоя можно определить из условия сохранения постоянства перепада давления в псевдоожиженном слое:

Рисунок 4.2 – Зависимость высоты слоя от скорости сплошной фазы

Рисунок 4.1 – Зависимость гидравлического сопротивления от скорости потока жидкости (или газа) в монодисперсном слое частиц.