Добавил:

ByeTPU Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

Системы управления химико-технологическими процессами

Файл:

LR8

.pdf

Скачиваний:

Добавлен:

25.06.2025

Размер:

588.32 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Цель работы:

1.Ознакомиться с методикой исследования звена второго порядка.

2.Получить практические навыки исследования звена второго порядка с помощью ЭВМ.

4.2.2. Звено второго порядка

Звено второго порядка описывается уравнением

T 2	d	2	y		dy
	d		y	+ T	dy	+ y = Kx
				+ T		+ y = Kx
2	d		2	1	d	,	(4.1)
	d				d

где Т1 и Т2 – постоянные времени.

Статическая характеристика звена второго порядка

y	0

Kx	0

Применим к уравнению (4.1) операцию прямого преобразования Лапласа:

T 2 p2 y(p)+T py(p)+
2	1
T 2 p2	+T p +1 y(p)=
2	1

y(p Kx(

)= Kx(
p)	.

)

;

(4.2)

Решение в операторной форме может быть записано в виде

y(p)=	T	2	p	2


	2

K +T1 p

x(p)

. (4.3)

Передаточная функция определяется выражением

W (p)=	y(p)	=
W (p)=	x(p)	=
	x(p)	T 2 p2
		2

K + T1 p

(4.4)

Используя операцию обратного преобразования Лапласа, выразим временную характеристику из уравнения (4.4):

−1

h( )= L

+ T p +1 p

p +

p2 + T1

Запишем характеристическое уравнение:

T 2

T 2 2

p +


1
1

p

		.	(4.5)
		.	(4.5)
	1		= 0

T 2
	2		.

Выразим корни характеристического уравнения:

				T					T		2						1
p	= −			T					T					−			1
p	= −			1						1				−
1,2			2T		2				4T			4				T		2
					2							4						2

				2							2						2		.											(4.6)
																			.											(4.6)
В зависимости от вида корней уравнение (4.5) меняет свои свойства.
Рассмотрим различные случаи решения уравнения 4.5).
Корни уравнения (4.6) действительные, разные
									T				2							T
									T
										1					4
										1					4						1			2
																					1
									T											T
									T
В случае, если										2									и									, то корни уравнения (4.6)
В случае, если																			и		2							, то корни уравнения (4.6)
																					2
																					T	2						1
																					T							1
																					1				−					0
																				4T			4		−			T	2	0
																							4						2

действительные, разные, так как																						2						2		. В общем случае получаем
действительные, разные, так как																														. В общем случае получаем
корни уравнения:						p		= −							и			p		= −							.
корни уравнения:							1					1			и				2						2		.
							1					1							2						2
Используя теорему Безу, запишем уравнение (4.5) в виде
h( )=		K			−1									1								1
h( )=		T	2	L			(p		− p )(p − p												)	p
		T					(p		− p )(p − p												)	p
												1								2
		2										1								2						.				(4.7)
																										.				(4.7)
Для решения уравнения (4.7) воспользуемся теоремой разложения
h( )=		B(0)			+	p				B(p				j	)			e	p j
		B(0)												j			)		p j
		A(0)									A (p						)

										j						j					.
																					.

В рассматриваемом случае:

В(рj) = 1;

А(рj) = (p–p1)(p–p2)=p2–(p1+p2)p+p1p2;

А (р) = 2р–р1–р2; 4.8

)

А (р1) = 2р1–р1–р2 = р1–р2; А (р2) = 2р2–р1–р2 = р2–р1.

Учитывая (4.8), запишем выражение для временной характеристики:

h( )=

T 2

p1(p1 − p2 )

p2 (p2 − p1)

p1 p2

(4.9)

Из уравнения (4.6) распишем выражение для произведения р1р2:

									T					T	2				1			T					T	2					1
p p					=		−		T	+				T				−	1	−		T			−		T			−			1		=
p p		2			=		−		1	+				1				−		−		1			−		1			−					=
	1	2						2T 2					4T			4			T 2			2T	2			4T			4			T		2
								2T 2					4T			4			T 2			2T	2			4T			4			T		2
									2						2				2			2						2					2
	T		2				T			T	2					1				T		T	2			1				T		2				1			1
	T						T			T						1				T		T				1				T						1			1
=	1					−		1		1				−					+	1		1			−				−		1				+			=
=				4		−			2			4		−				2	+		2			4	−		2		−				4		+		2	=		2
	4T			4			2T		2	4T		4				T		2	2T		2	4T		4		T	2			4T			4			T	2		T	2	.
	4T						2T			4T						T			2T			4T				T				4T						T			T		.
			2					2			2						2			2			2			2						2				2			2

(4.10)

Подставляя выражение (4.10) в уравнение (4.9), запишем общий случай решения уравнения (4.5) для случая простых корней:

h( )= K

− p

)

−

p	)
1

e	p	2
	p

(4.11)

Для рассматриваемого случая корни уравнения должны быть разные (не должно быть кратных и нулевых корней). Подставим в уравнение (4.11) вещественные корни р1 = – 1 и р2 = – 2:

h( )= K

−

e−1

−

e−2

−

(4.12)

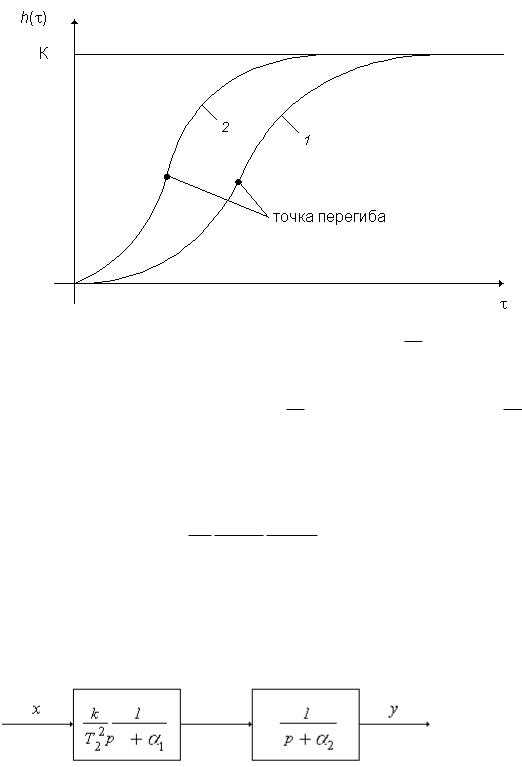
Графическая интерпретация уравнения (4.12) представлена на рис. 4.9, кривая 1.

Запишем выражение для передаточной функции:

W (p)=	K	=	K
W (p)=		=	T 2
T 2 p2	+T p +1		T 2
2	1		2

(p −

1 p1)(p −

)

									T	2
									1	2
									1
Рис. 4.9. Временные характеристики для случаев, когда									T	:
Рис. 4.9. Временные характеристики для случаев, когда									2	:
									2
						T	2				T	= 2
						1	2				1	= 2
						1					1
1 – корни действительные, разные,						T		; 2 – корни кратные,			T
1 – корни действительные, разные,						2		; 2 – корни кратные,			2
						2					2
Учитывая, что р1 = – 1 и р2 = – 2, выражение для передаточной
	W (p)=	K		1		1
	W (p)=	T	2	p +	p +
		T		p +	p +
				1			2
функции примет вид:		2		1			2	, т. е. звено представляет
функции примет вид:								, т. е. звено представляет

собой последовательное соединение двух апериодических звеньев (рис. 4.10), поэтому оно не относится к элементарным типовым звеньям и его можно описать системой из двух дифференциальных уравнений.

Рис. 4.10. Структурная схема передаточной функции для случая, когда корни действительные, разные

Уравнение (4.6) имеет кратные корни

p	= p		= −	Т
p	= p	2	= −	1
1		2		2
				2Т
				2

= −

, когда

T	2			1							T
T				1
1
1			−			= 0					1	=
		4			2						1
4T				T							T


	2			2			и, следовательно,				2
							и, следовательно,
определяется выражением:
			W ( p) =					K			= T 2

							T 2	(p − p )(p − p	2	)			(
						2		1	2			2

2
. Передаточная функция
K
p + )(p + ),	(4.13)

т. е. звено представляет собой последовательное соединение двух апериодических звеньев с одинаковыми временными функциями.

В случае, когда уравнение (4.6) имеет кратные корни, временная характеристика определяется уравнением

h( ) =	K	L−1	1	1		= K 1− e−(1+ )

			(p + )2
T 2					p
2						.	(4.14)

Графическая интерпретация уравнения (4.14) представлена на рис. 4.9, кривая 2.

Уравнение (4.6) имеет два комплексных сопряженных корня

Рассматриваемый случай возможен, когда подкоренное выражение в

			T12			1				T
										1
			4T		4 − T 2 0					1	2
уравнении (4.6)			4T		4 − T 2 0				T		2
уравнении (4.6)				2		2		, т. е.	2			. Корни уравнения (4.6)
определяются выражением
	T1
p = −	T1			i 1 T			2	−T 2	4T 4
p = −				i 1 T				−T 2	4T 4
1,2	2T 2					2		1	2
	2T 2										(4.15)
		2									(4.15)
или в общем случае:
p1,2 = − i					.						(4.16)
					.						(4.16)

Так как полюсы разные, то можно воспользоваться уравнением (4.11) для записи выражения временной функции

e p1 +

e p2

h( )= K 1+

(p − p

)

− p

После подстановки выражения (4.16) в (4.11) получим

h( )= K 1+

− −i

e(−+i ) +

− + i

e(− −i )

− + i + + i

− −i + −i

Преобразуя данное выражение, получим выражение для временной

характеристики:

h( )= K 1− ce− sin ( + )

(4.17)

c =
	1 −
где

Графическая

2


		= arctg

	,

интерпретация



	.
	.

уравнения (4.17) представлена на рис.

h( )

c e	−

А1

А2

4.11.

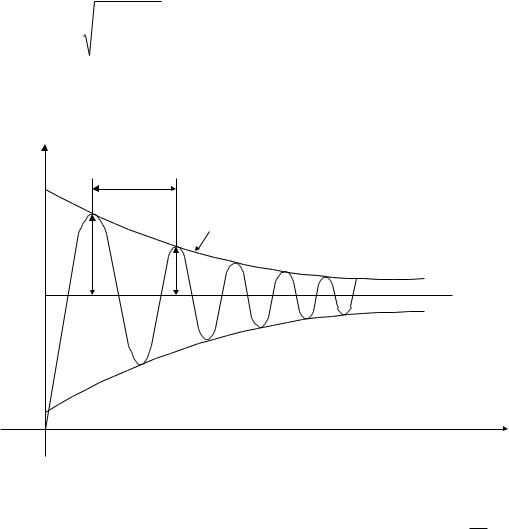
Рис. 4.11. Временная характеристика для случая, когда

	T	2
	1	2
	1
	T
	2

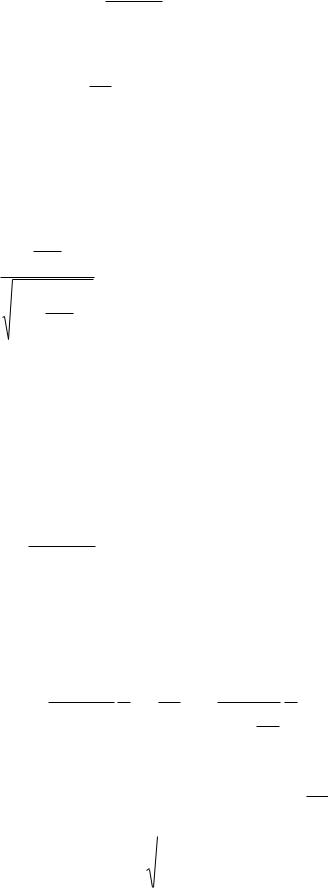
С помощью значений амплитуд колебаний можно оценить величину

								A − A
					=			1	2
					=				A
степени затухания									A	, которая в общем случае изменяется
степени затухания									1	, которая в общем случае изменяется
									1
в интервале 0 1. Амплитуда А2											может быть определена из выражения
		−T		T =			2
A	= A e	−T		T =
A	= A e		, где					. Используя выражения для А2 и Т, выражение для
2	1


степени затухания преобразуется к виду =1− e−2 m , где m = –
корневой показатель колебательности или степень колебательности.
Учитывая уравнения (4.15) и (4.16), получим
			T
				1
			2T
	m =			2
	m =					2
				T		2
				T
			1−	1
				2T
				2T
				2			.				(4.18)
							.				(4.18)

Уравнение (4.6) имеет два чисто мнимых корня

Рассматриваемый случай возможен, когда Т1 = 0.

Выражение для передаточной функции звена будет иметь вид

W (p) =			K
	T	2	p	2


	2

(4.19)

Применяя к уравнению (4.19) операцию обратного преобразования Лапласа, запишем выражение для временной характеристики:


−1				K		1		K		−1				1				1
							=

h( )= L			2	p	2			T	2	L			2			1
	T		2	p	2	+1 p		T	2				2			1		p
		2						2				p		+			2
															T		2
															T
																2
																	p2 +
Из уравнения (4.20) следует, что при

						p =		−		1	= i				1
						p =		−			= i
						1,2			T 2					T2
чисто мнимых корня:									T 2					T2		.
чисто мнимых корня:										2						.

T22

(4.20)

= 0

существует два

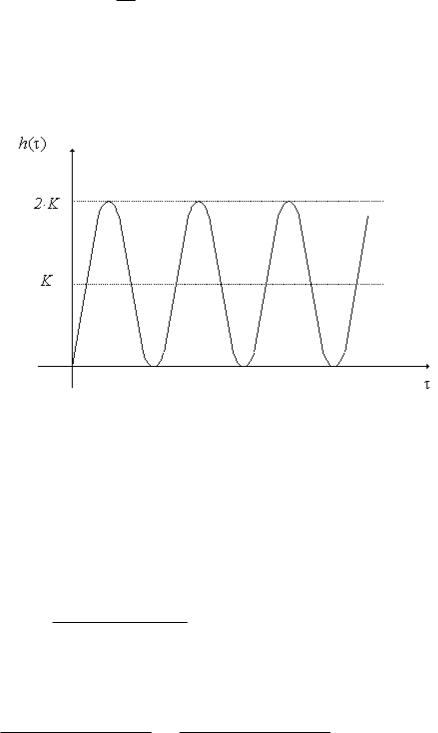
Спомощью теоремы разложения уравнение (4.20) преобразуется

квиду

		1
h( ) = K 1	− cos
		T
		T
		2



(4.21)

В данном случае имеем косинусоиду с постоянной амплитудой (см. рис. 4.12). Такое колебательное звено получило название консервативного.

Рис. 4.12. Временная характеристика для случая, когда Т1 = 0

Частотные характеристики звеньев второго порядка

Формально частотную характеристику можно получить из передаточной функции (4.4) путем подстановки p = i :

W (i ) =														K							=
W (i ) =				− T					2				2	+ T i +1							=
									2				2

								2									1
					K (1 − T											2		2	)− iT
					K (1 − T														)− iT
=	(1 − T														2						1								=
=			2			2			)+ iT (1 − T												2	2		)− iT					=
			2			2															2	2

		2												1						2							1
	K (1 − T										2			2	)										KT
	K (1 − T														)										KT
=										2								− i									1				.
=									2									− i									2				.
		2			2				2						2		2						2			2	2			2	2
	(1 − T	2			2		)					+ T			2		2			(1 − T			2			2	)	+ T		2	2
	(1 − T						)					+ T								(1 − T							)	+ T
	2													1								2							1

(4.22)

Из (4.22) можно получить амплитудно-частотную и фазо-частотную характеристики:

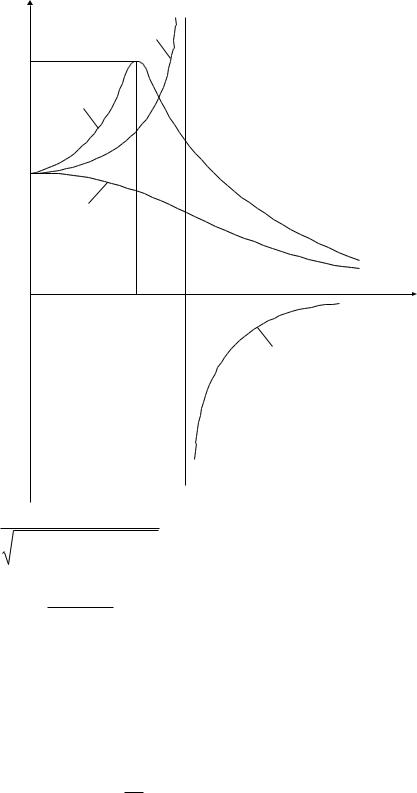
A( )

в Amax

	1
	T
	2
р
	в

A( ) =			K
A( ) =					2
		2		2	2			2	2
	(1 − T	2		2	)	+ T		2	2
	(1 − T				)	+ T
	2						1		;
									;
			T
( )= −arctg				1
( )= −arctg					2		2
	1 −T				2		2
	1 −T
				2			.
							.

В зависимости от соотношения Т1 и Т2 амплитудно-частотная характеристика имеет различный вид:

Рис. 4.13. Амплитудно-частотные характеристики звеньев второго порядка

1.Для случаев, когда T2 , амплитудно-частотная характеристика1

монотонно убывающая (см. рис. 4.13, а).

		T
		1
		T
2. Для случая, когда		T
2. Для случая, когда		2
		2



	A
		max



имеет максимум
имеет максимум

резонансной частоте

, амплитудно-частотная характеристика

= A(			)=			K
						K
		p
			T					T
			1		1 −			1
			T				2T
			T				2T
			2					2
		1		1 T				2
		1		1 T
р	=		1 −			1
р		T		2		T
		T		2		T
		2				2





	2



			при некоторой
			при некоторой

(рис. 4.13, б).

Колебательные свойства звена 2-го порядка можно оценить по величине Аmax: чем больше Amax, тем колебательность звена больше. Для оценки колебательности существует частотный показатель колебательности

	A(	)		T
M =	p		=		2
M =	A(0)		=				2
	A(0)					T	2
			T	1 −		T
			T	1 −		1
			1			2T
						2T
						2	.		(4.23)
							.		(4.23)
									1 + m	2
								M =	1 + m
								M =	2m
Сравнивая (4.18) и (4.23), получим									2m	.
Сравнивая (4.18) и (4.23), получим										.

3. Для случая, когда Т1 = 0 амплитудно-частотная характеристика

определяется выражением

A( )= U ( )=	K
	1 −T	2	2


	2

(см. рис. 4.13, в).

Результаты снятия и обработка данных

Исходные данные

1 / 21 2 > Следующая >>>

Соседние файлы в предмете Системы управления химико-технологическими процессами

#
25.06.2025681.62 Кб0LR5 .pdf
#
25.06.2025588.32 Кб0LR8.pdf
#
25.06.2025719.6 Кб0LR9-10 АСП .pdf
#
25.06.2025682.09 Кб1ЛБ 1.pdf
#
25.06.2025700.06 Кб0ЛБ 2.pdf
#
25.06.2025289.45 Кб0ЛБ 3 .pdf
#
25.06.2025469.21 Кб0ЛБ 4 .pdf