
LR5
.pdf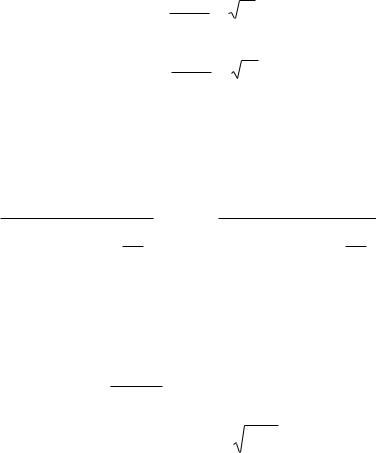
и переходная функция рассчитывается по формуле
y(t) = K (1 − e |
−t |
(1 |
+ t |
|
Если D > 0, то корни вещественные разные
)).
|
|
|
a |
|
|
||
1 |
= −1 |
= − |
|
1 |
− |
D , |
|
P |
|
|
2 |
a |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
a |
|
|
|
P2 |
= −2 |
= − |
|
1 |
+ |
D . |
|
2 |
a |
||||||
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
Используя теорему разложения Хевисайда, получим уравнение переходной функции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t) = K |
|
1 |
+ |
|
|
|
1 |
|
|
P |
t |
|
|
|
|
|
a |
|
e 1 |
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
a |
|
P |
2 P + |
|
|
|||
|
|
2 |
|
1 |
|
|
|
||||
|
|
|
|
1 |
|
1 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
1 |
|
|
|
e |
P |
t |
|
|
|
|
|
a |
|
2 |
|
||
a |
|
P |
2 P |
+ |
|
|
|
|||
2 |
|
1 |
|
|
|
|
||||
|
2 |
|
2 |
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
Точность аппроксимации экспериментальной кривой разгона решением дифференциального уравнения оценивается по величине остаточной дисперсии
S |
2 |
= |
1 |
|
|
|
|||||
ост |
M − N |
||||
|
|
|
|||
|
|
|
|
и по среднеквадратичному отклонению
M |
|
2 |
|
(z j − y j ) |
|||
|
|||
j =1 |
|
|
|
СКО = |
2 |
||
S |
|
||
|
ост |
||
.
9. Результаты снятия и обработка экспериментальной кривой разгона
Исходные данные приведены в таблице 1.
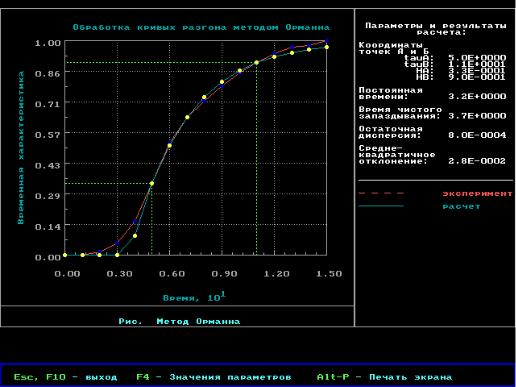
Таблица 1 – Исходные данные
|
|
Вариант 3 |
|
|
|
|
|
|
( ) |
|
( )/ (15) |
|
|
|
|
0 |
0 |
|
0 |
1 |
0 |
|
0 |
2 |
0,15 |
|
0,015384615 |
3 |
0,55 |
|
0,056410256 |
4 |
1,55 |
|
0,158974359 |
5 |
3,25 |
|
0,333333333(А) |
6 |
5,1 |
|
0,523076923 |
7 |
6,25 |
|
0,641025641 |
8 |
7 |
|
0,717948718 |
9 |
7,7 |
|
0,78974359 |
10 |
8,3 |
|
0,851282051 |
11 |
8,75 |
|
0,897435897(Б) |
12 |
9,15 |
|
0,938461538 |
13 |
9,45 |
|
0,969230769 |
14 |
9,55 |
|
0,979487179 |
15 |
9,75 |
|
1 |
С помощью аппроксимирующих программ для метода Ормана, метода кратных корней 2-го, 3-го и 4-го порядков, метода Симою выполнили расчеты параметров аппроксимирующих уравнений. Результаты расчетов для каждого метода представлены на рисунках 5-9 и в таблице 2.
Рисунок 5 – Результаты обработки кривой разгона методом Орманна
Согласно полученным данным, постоянная времени и время чистого запоздания соответственно равны 3,2 и 3,7. Тогда, аппроксимирующее уравнение будет иметь следующий вид
( ) = 0,333; 0 ≤ ≤ 3,7;
{ |
− −3,2 |
( ) = 3,25 ∙ [1 − |
3,7 ] ∙ К ; > 3,7 |
|
об |
Рисунок 6 – Результаты обработки кривой разгона методом кратных корней (порядок уравнения – 2)
Из рисунка 6 видно, что об = 2,6 |
|
и = 2. Аппроксимирующее |
||||||||
уравнение: |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|||
|
|
|
∙ − |
|||||||
h(t) = 3,25 ∙ [1 − ∑ |
|
|
∙ |
|
2,6 |
] |
||||
2,6 |
! |
|||||||||
|
|
|
|
|
||||||
=0
Аналогично определили вид аппроксимирующего уравнения для уравнений 3-го и 4-го порядков.
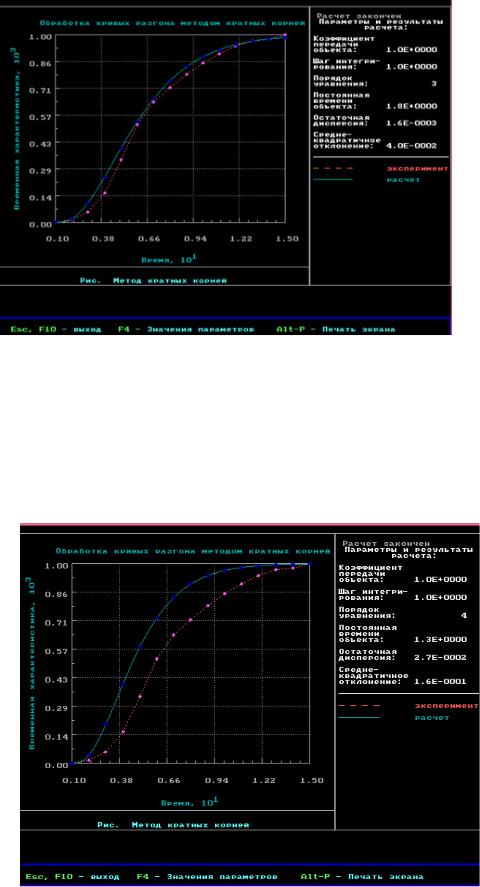
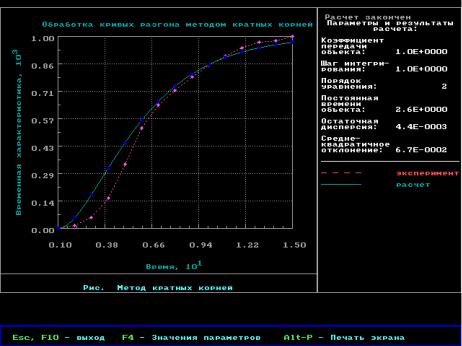
Рисунок 7 – Результаты обработки кривой разгона методом кратных корней (порядок уравнения – 3)
Из рисунка 7 видно, что об = 1,8 и = 3. Аппроксимирующее уравнение:
2 |
|
|
|
1 |
|
|
|
||
|
|
|
∙ − |
||||||
h(t) = 3,25 ∙ [1 − ∑ |
|
∙ |
|
1,8 |
] |
||||
1,8 |
! |
||||||||
|
|
|
|
|
|||||
=0
Рисунок 8 – Результаты обработки кривой разгона методом кратных корней (порядок уравнения – 4)
Из рисунка 7 видно, что об = 1,3 |
|
и |
= 4. Аппроксимирующее |
||||||
уравнение: |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
||
|
|
|
∙ − |
||||||
h(t) = 3,25 ∙ [1 − ∑ |
|
∙ |
|
1,3 |
] |
||||
1,3 |
! |
||||||||
|
|
|
|
|
|||||
=0
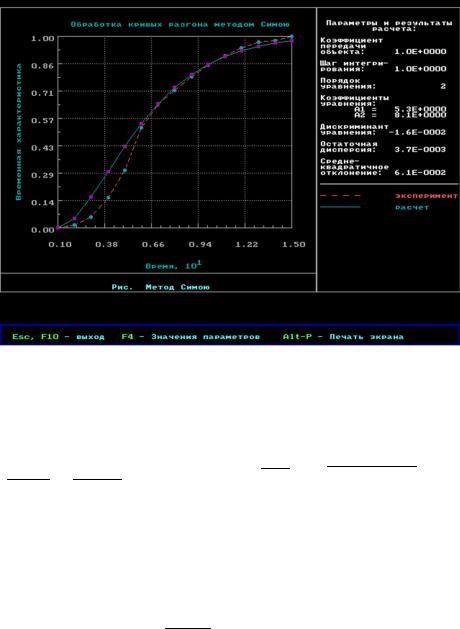
Рисунок 9 – Результаты обработки кривой разгона методом Симою Как видно из рисунка 9, коэффициенты уравнения 1 = 5,3 и 2 = 8,1, а
< 0. Следовательно, корни комплексные
= 2 ∙ 1 2 = 25,3∙ 8,1 = 0,327; = √− = √−(−0,016) = 0,126;
1,2 = −0,327 ± ∙ 0,126
Переходная функция
( ) = 1 − −0,327∙ ∙ (0,1260,327 ∙ sin(0,126 ∙ ) + cos(0,126 ∙ )).
Сравним все методы в таблице 2.
Таблица 2 – Сравнительный анализ результатов аппроксимации экспериментальной кривой разгона различными методами
Метод |
П.у. |
Вид аппроксимирующего уравнения |
Показатели качества |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Остаточн. |
Средне- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дисперсия |
квадрат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отклонен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ие |
|
Метод |
|
( ) = 0,333; 0 |
≤ ≤ 3,7; |
|
|
|
|
|||||||||
1 |
{ ( ) = 3,25 ∙ [1 − − |
−3,2 |
|
|
|
|
|
|
|
0,0008 |
0,028 |
|||||
Орманна |
3,7 ] ∙ Коб; |
> 3,7 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
− |
|
|
||||||
|
|
h(t) = 3,25 ∙ [1 − ∑ |
|
|
|
∙ |
∙ |
2,6 |
] |
|
|
|||||
|
2 |
|
2,6 |
! |
0,0044 |
0,067 |
||||||||||
|
=0 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Метод |
|
|
|
|
|
|
|
− |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
h(t) = 3,25 ∙ [1 − ∑ |
|
|
|
|
∙ |
|
∙ |
1,8] |
|
|
|||||
кратных |
3 |
|
1,8 |
! |
|
0,0016 |
0,04 |
|||||||||
=0 |
|
|
|
|
|
|
||||||||||
корней |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
− |
|
|
||||||
|
|
h(t) = 3,25 ∙ [1 − ∑ |
|
|
|
∙ |
∙ |
1,3 |
] |
|
|
|||||
|
4 |
|
1,3 |
! |
0,027 |
0,16 |
||||||||||
|
=0 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
( ) = 1 − −0,327∙ ∙ ( |
0,126 |
∙ |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
Метод |
|
|
|
0,327 |
|
|
|
|
|
|
||||||
2 |
∙ sin(0,126 ∙ ) + cos(0,126 ∙ )) |
0,0037 |
0,061 |
|||||||||||||
Симою |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод
В ходе лабораторной работы ознакомились с методикой проведения эксперимента по снятию кривых разгона и последующей их обработкой. Наиболее точная аппроксимация экспериментальной кривой разгона была достигнута методом Орманна, поскольку в данном случае наблюдаются минимальные значения остаточной дисперсии (0,0008) и среднеквадратичного отклонения (0,028). Наименее точным метод оказался «метод квадратных
корней» 4 порядка ( 2 |
= 0,027, СКО = 0,16). |
||
ост |
|
|
|
Таким образом, рекомендуемое аппроксимирующее уравнение: |
|||
|
( ) = 0,333; |
0 ≤ ≤ 3,7; |
|
{ |
|
− −3,2 |
|
( ) = 3,25 ∙ [1 − |
|
3,7 ] ∙ К ; > 3,7 |
|
|
|
|
об |
