Добавил:

ByeTPU Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

Системы управления химико-технологическими процессами

Файл:

LR9-10 АСП

.pdf

Скачиваний:

Добавлен:

25.06.2025

Размер:

719.6 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

возмущения больше 1000, при Кр=0,046 по каналу управления 415,9 по каналу возмущения 667,3, при Кр=0,069 по каналу управления 667,3, по каналу возмущения 524,3.

У систем с ПИ-регулятором статическая ошибка минимальна и близка к нулю по каналу управления 0,003, по каналу возмущения 0,0025.

По полученным данным, также можно наблюдать то, что минимальная динамическая ошибка чаще всего наблюдалась у П-регулятора при Кр=1,3 по каналу управления 0,18, по каналу возмущения 0,4913, при Кр=2,5 по каналу управления 0,405, по каналу возмущения 0,5852, соответственно и время регулирование было также минимальным при Кр=1,3 по каналу управления

193,6, по каналу возмущения 274,4, при Кр=2,5 по каналу управления 447,8, по каналу возмущения 501,0. Однако это не компенсирует более высокую статистическую ошибку по сравнению регуляторами И и ПИ, поэтому использование П-регулятора не рекомендуется в этих условиях.

Наиболее подходящим является ПИ регулятор с параметром настройки Кр=0,021 , Ти = 59,052

Цель работы заключается в следующем:

1.Получить практические навыки расчета настройки автоматических систем регулирования с помощью ЭВМ.

2.Получить практические навыки моделирования и исследования автоматических систем регулирования с помощью ЭВМ.

4.4.4.2. Расчет одноконтурных АСР

В практике расчета настройки автоматических систем регулирования широкое распространение получил метод Циглера – Никольса из-за своей простоты и легкости алгоритмизации.В соответствии с этим методом расчет настроек регуляторов проводят в два этапа:

•рассчитывается критическая частота пропорциональной составляющей

Кркр, при которой АСР будет находиться на границе устойчивости, и соответствующую ей критическую частоту кр;

•по найденным значениям Кркр и кр определяются оптимальные настройки,

обеспечивающие	степень	затухания	переходного	процесса
= 0,8 0,9.

Уравнения для расчета Кркр и кр получают из известных уравнений для П- регулятора [17, 18]:

A		(		)К	р	=1
об			кр		р
					кр		;	(4.34)
							;	(4.34)
	об		( )+ = 0				.	(4.35)
							.	(4.35)

Оптимальные настройки регуляторов находятся по следующим соотношениям
[17]:
			• для П-регулятора Wp (P)= Kp ;
K	p	опт	= 0,5K	p	кр	(4.36)
	p			p

					;

Kpопт

С0опт

Kpопт

С0опт

				W	(P
•	для ПИ-регулятора			p
•	для ПИ-регулятора
0,45K		p
		кр
		;
0,086Kpкр кр			.
			.

		W
•	для ПИД-регулятора	p
•	для ПИД-регулятора

			С
)= K	p	+	0
)= K		+	Р

(4.37)

(4.38)

(P)= K	p	+
	p

0,45Kp				(4.39)
кр ;				(4.39)
0,192Kp	кр	кр	;	(4.40)
	кр

;

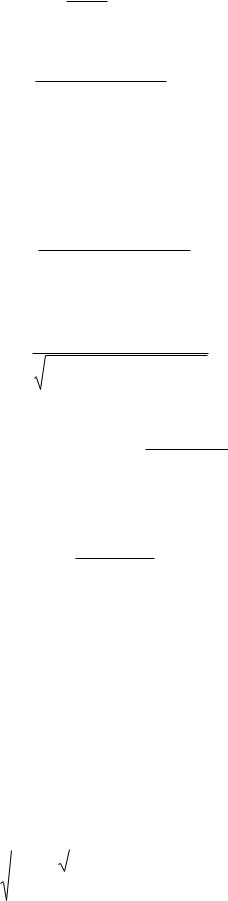
С0 Р

+Т Д

;

			K
			p
T		= 0,471	кр
T		= 0,471
Д
	опт
			кр	.
				.

Пусть динамические свойства

(4.41)

объекта заданы в виде передаточной функции

W	(P) =				К	об			е−Р об
W	(P) =					об			е−Р об
об	Т	2	Р	2	+ Т		Р + Т
		2		2
		2						3
		2				1		3	,	(4.42)
									,	(4.42)

для которой можно построить различные модели объектов, получаемых при аппроксимации экспериментальных и аналитических временных характеристик.

Из	выражения			(4.42)			путем замены			Р = i формально можно получить
выражение для комплексной частотной характеристики:
W	(i )=				К	об			е−i об
		2		2
об	Т				+ Т i + Т
		2	(i )					3
						1			.	(4.43)

Отсюда амплитудно-частотная характеристика объекта может быть получена в виде

А	( ) =				К	об
А	( ) =					об
об								2
					2		2	2		2	2
		(Т		−Т	2		2	)	+Т	2	2
		(Т	3	−Т	2			)	+Т	1	,	(4.44)
			3		2					1

а фазо-частотная характеристика объекта может быть получена в виде

	( ) = −					Т
об	( ) = −	об	− arctg			1
						1
				Т		−Т	2	2
				Т	3	−Т	2
					3		2

Подставив выражение (4.45) в критической частоты:

  

.	(4.45)
(4.35),	получим уравнение для расчета

				T
−	об	− arctg		1			+ = 0
−		− arctg			2	2	+ = 0
			T	−T	2	2
			T	−T
			3	2			.	(4.46)
							.	(4.46)

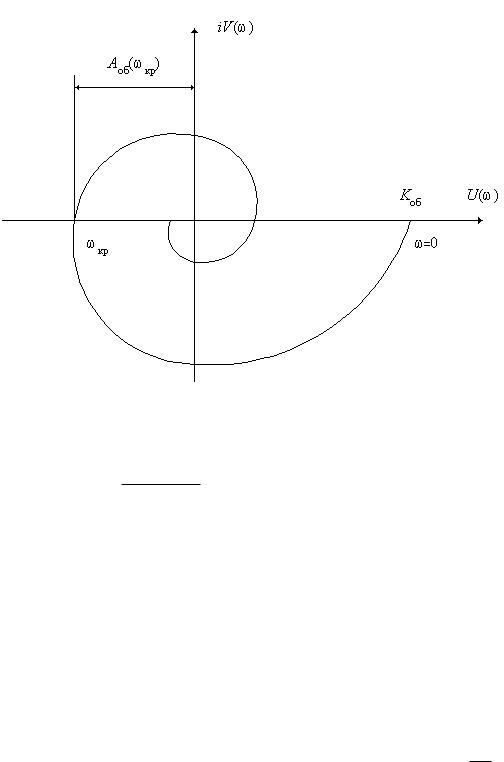
Комплексная частотная характеристика объекта пересекает отрицательную вещественную полуось бесконечное число раз, так как уравнение (4.46) относится к виду трансцендентных (см. рис. 4.20).

Для расчета критической частоты из уравнения (4.46) нужно определите только один корень, например с помощью метода дихотомии.

Начальный шаг изменения частоты и начальное значение частоты н нужно выбрать так, чтобы выполнялось неравенство

Т		Т	2	2
	3		2	.	(4.47)

Так, представляет интерес вычислять значения кр из уравнения (4.46) при минимальном числе шагов. Начальное значение частоты можно выбирать, ориентируясь на величину


р =		Т3	=	Т3
р =	Т 2		=	Т2	.	(4.48)
	Т 2			Т2
	2


	p	об	2
Если при данной частоте				, то начальное значение частоты	н

нужно взять меньше р или делать отрицательные приращения частоты , контролируя невязку решения уравнения (4.46).

Рис. 4.20.

График комплексной частотной характеристики объекта В результате находят решения уравнения (4.46) до тех пор, пока не выполнится условие

				T	p
−			− arctg	1	p		+
−	p	об	− arctg		2	2	+
	p	об	T	− T
			T	− T
			3	2		p	,	(4.49)
							,	(4.49)

находится значение критической частоты кр, и по выражению (4.34) с учетом (4.44) рассчитывается критическое значение настройки П-регулятора (Кркр), а по выражениям (4.36)–(4.41) рассчитываются оптимальные параметры настройки регуляторов.

4.4.3. Исследование переходных процессов в одноконтурной АСР

Расчет переходных процессов в одноконтурной АСР можно выполнить путем численного интегрирования системы дифференциальных уравнений, представленных в нормальной форме Коши.

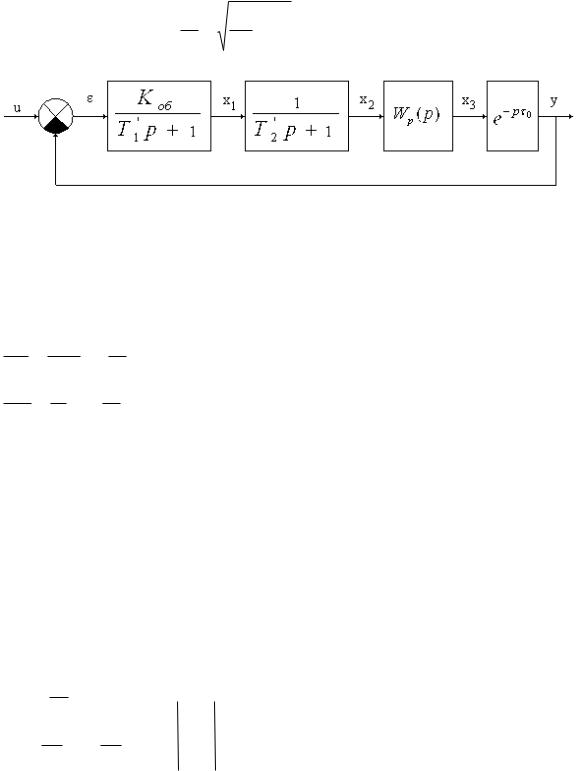
Передаточная функция (4.42) может быть представлена в виде произведения

двух передаточных функций апериодических звеньев при

Wоб ( p) =	Kоб	1		e	− p об
	(Т1 p +1)	(T2 p	+1)		,	(4.50)

Т Т

1 2

и Т3 = 1:

	Т	=	Т
	Т	=	1
где	1		2
			2

Тогда структурная схема

	2
	Т		2
+	1	−Т	2
+	4	−Т	2		Т	=
					Т	=
				;	2
					2

АСР будет иметь

Т	1	−
	1

вид,

Т	.	(4.51)
1

представленный на рис. 4.21.

Рис.

4.21. Структурная схема одноконтурной АСР Путем введения промежуточных переменных динамические свойства объекта

и регулятора приводятся к нормальной форме Коши.

Для системы с П-регулятором:

=U − y( );

об −

;

−

;

x = K

;

y( ) = x

( −

об

(4.52)

Если систему дифференциальных уравнений записать в векторной форме, то

система (4.52) примет вид:

− y( );

( ) =

Ax( )

+ B ( );

= K

;

( −

y( ) = x

об

(4.53)

где

−

А =

об

−

В = Т

;

(4.54)

Интегрирование системы дифференциальных уравнений может быть осуществлено по методу Рунге – Кутта.

Для системы с ПИ-регулятором:

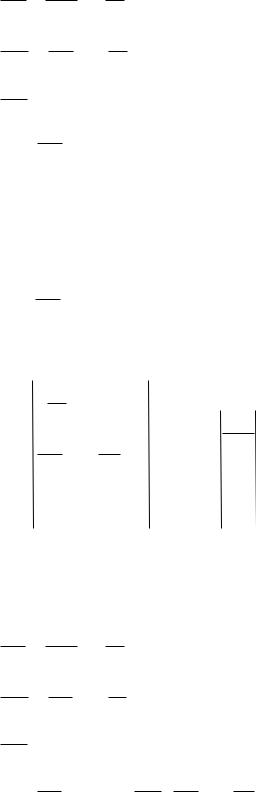
=U − y( );

об −

;

1 =

Кр

−

;

= x

;

+ x

;

y( ) = x

( −

об

)

или в векторной форме

− y( );

( )

= Ax( )

+ B ( );

;

+ x

( −

y( )

= x

об

где

−

Кр

об

А =

−

В =

;

Для системы с ПИД-регулятором:

= U − y( );

об −

;

Кр

−

;

= x

;

Кр

x =

0 x

+ x

−

;

y( ) = x

( −

об

)

или в векторной форме

(4.55)

(4.56)

(4.57)

(4.58)

= U − y( );

x( )

Ax( )

B ( );

x =

+ x

−

;

y( ) = x ( −

об

(4.59)

где

	−			1		0		0
	−		Т1			0		0	Коб
			Т1						Коб
		Кр					1
А =		Кр			−		1	0	Т1
									Т1
									0
		Т2				Т2		В =	0
			0			1		0	0
									0
								;	.	(4.60)

В табл. 4.1 представлены варианты исходных данных для выполнения лабораторной работы.

Таблица 4.1 Исходные данные для выполнения лабораторной работы

№	Наименование		Обозначен	Размерност	Численные
п/	данного		ие	ь	значения
п					I	II	III
1	Коэффициент		Коб		2,0	3,0	4,0
	усиления объекта
2	Постоянная		Т1	мин	10	20	30
	времени объекта Т1
3	Постоянная		Т2	мин	3	2	5
	времени объекта Т2
4	Постоянная Т3		Т3	мин	1	1	1
5	Время		об	мин	0,9	2,0	3,0
	запаздывания
6	Начальное		нач	1
6	Начальное		нач	мин
	значение частоты			мин
	значение частоты
7	Начальный	шаг	d	1
7	Начальный	шаг	d
	изменения частоты			мин
	изменения частоты
8	Точность	расчета		1
8	Точность	расчета
	критической			мин
	критической
	частоты

Ввод исходных данных осуществляется в следующем порядке:

1. Параметры объекта регулирования (Коб, Т1, Т2, Т3, Ков, Тов, об).

2.Исходные данные для расчета параметров настройки АСР (начальное значение частоты, начальный шаг изменения частоты, точность расчета критической частоты, вид передаточной функции).

3.Параметры регуляторов.

4.Параметры расчета:

•порядок системы дифференциальных уравнений n = 2 для системы с П- регулятором и n = 3 для систем ПИ и ПИД-регуляторами;

•длительность переходного процесса можно приближенно определить по формуле: tк = 5 ( об + Т1 + Т2);

•шаг интегрирования dt выбирается достаточно малым, однако, величина

шага должна удовлетворять условию:

	t
dt	к
м	1000
1

;

•периодичность вывода на экран м1 задается произвольно и представляет собой целое число (рекомендуемые значения: 1, 2, …, 10).

Практическая часть

Таблица 1 – Исходные данные

Данные:

Коэффициент усиления объекта Коб – 4,2

Постоянная времени объекта Т1, мин – 20

Постоянная времени объекта Т2, мин – 5

Время запаздывания объекта Т3, мин – 0,6

Коэффициент усиления объекта возмущения Ков – 2,1

Постоянная времени объекта возмущения Тов, мин – 5

Время запаздывания объекта регулирования , мин – 2,5

Допустимое значение частотного показателя колебательности Мдоп – 1,62

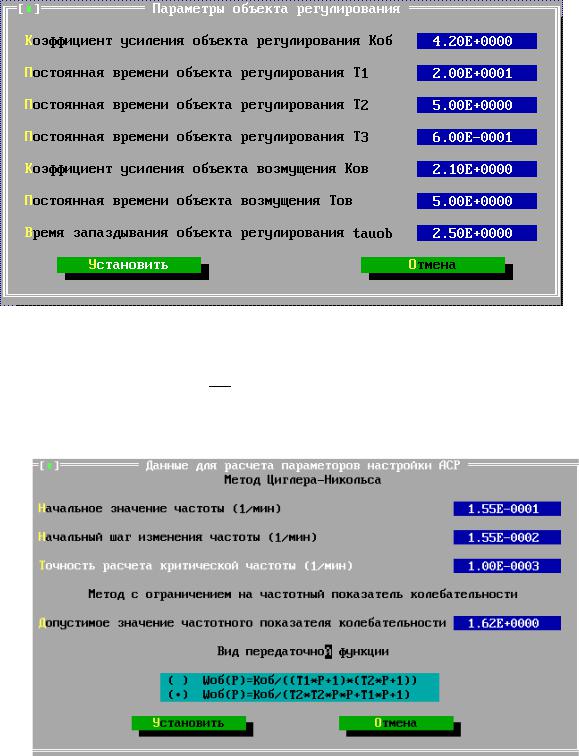
Рисунок 3 – Ввод параметров объекта регулирования Начальное значение частоты рассчитывается по следующей формуле:


= √	3	=	√ 3	=	√0.6	= 0.155
= √	2	=		=	5	= 0.155
	2				5
	2		2

Рисунок 4 – Данные для расчёта параметров настройки АСР

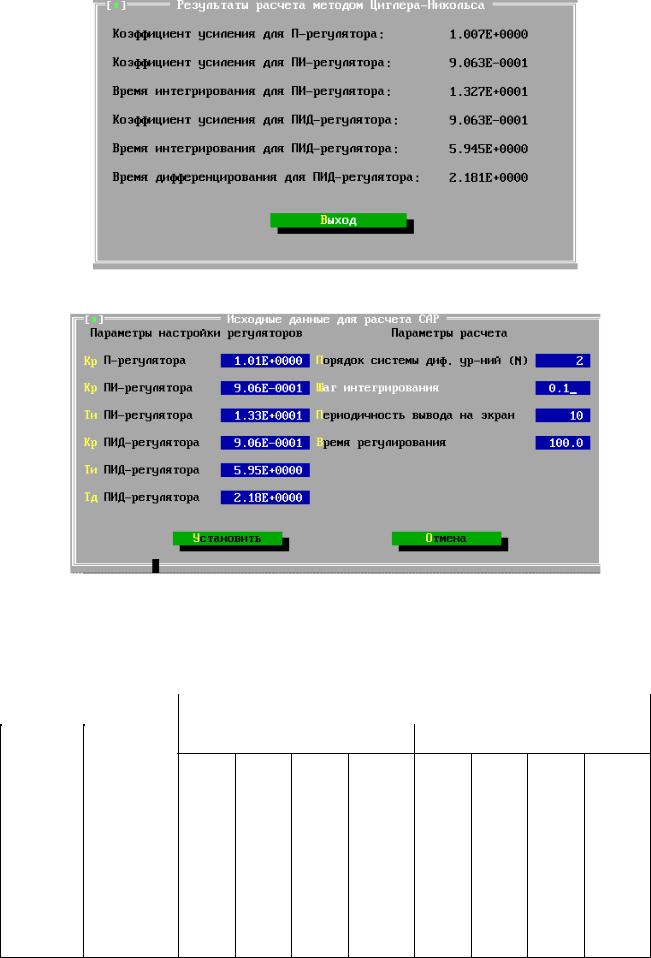
Рисунок 5 – Результаты расчёта методом Циглера-Никольса

Рисунок 6 – Исходные данные для расчёта АСР Таблица 2 – Результаты исследования одноконтурных АСР

		Оценки качества переходного процесса
Регулято	Параметры
Регулято	Параметры	Канал управления	Канал возмущения
		Канал управления	Канал возмущения

рнастройки

		Ад	Ψ	τр	∆ ст	Ад	Ψ	τр	∆ ст

П	Кр=1,01	0,222	0,934	43,36	0,19	0,830	0,942	49,81	0,40

ПИ	Кр=0,906	0,372	0,921	65,09	0,0015	1,237	0,986	79,26	0,0025
ПИ	t=13,3	0,372	0,921	65,09	0,0015	1,237	0,986	79,26	0,0025
	t=13,3

	Кр=0,906
ПИД	t=5,95	0,328	0,927	88,52	0,002	1,008	0,879	94,81	0,0025
	T=2,18

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете Системы управления химико-технологическими процессами

#
25.06.2025681.62 Кб0LR5 .pdf
#
25.06.2025588.32 Кб0LR8.pdf
#
25.06.2025719.6 Кб0LR9-10 АСП .pdf
#
25.06.2025682.09 Кб0ЛБ 1.pdf
#
25.06.2025700.06 Кб0ЛБ 2.pdf
#
25.06.2025289.45 Кб0ЛБ 3 .pdf
#
25.06.2025469.21 Кб0ЛБ 4 .pdf